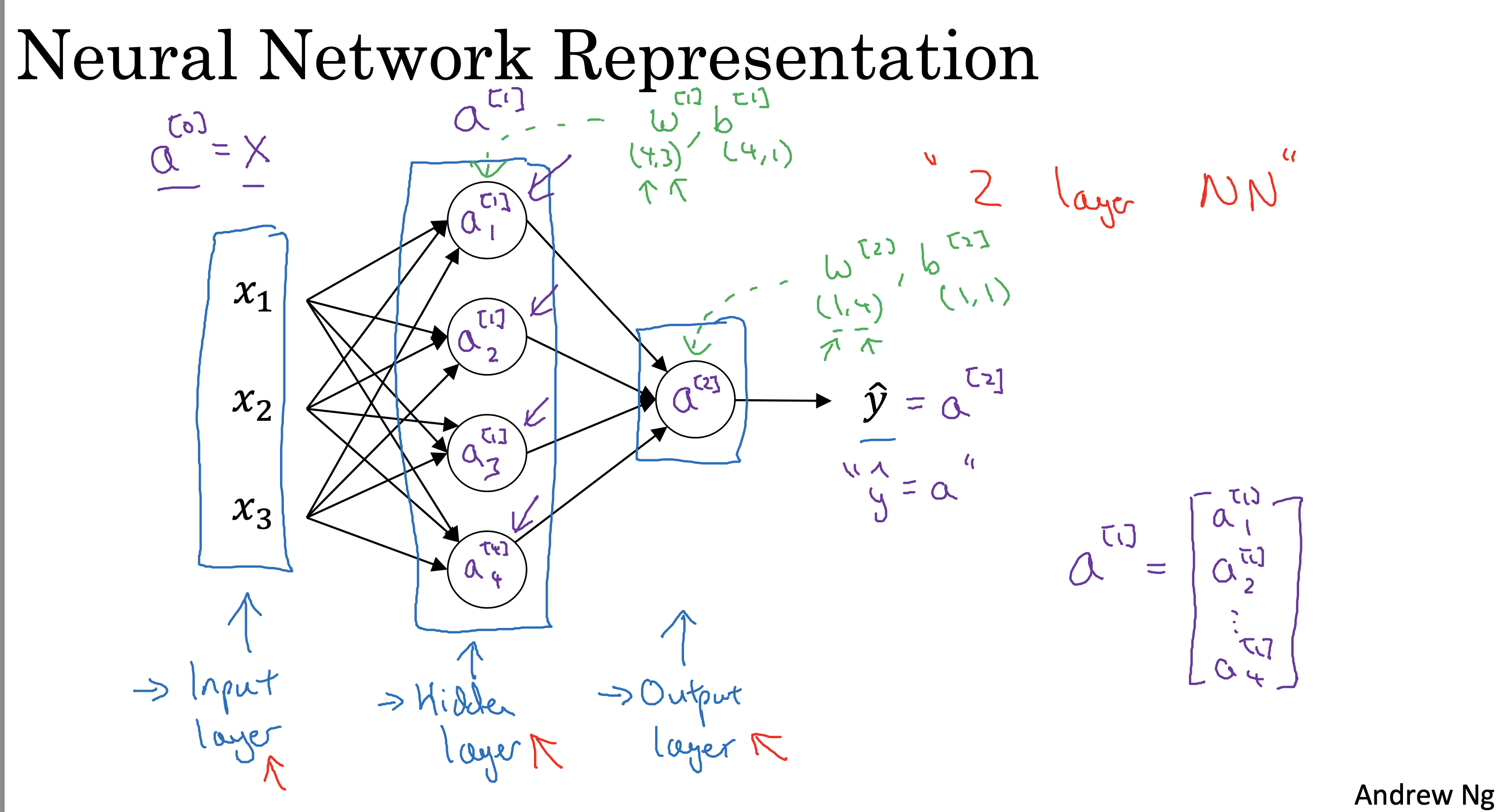
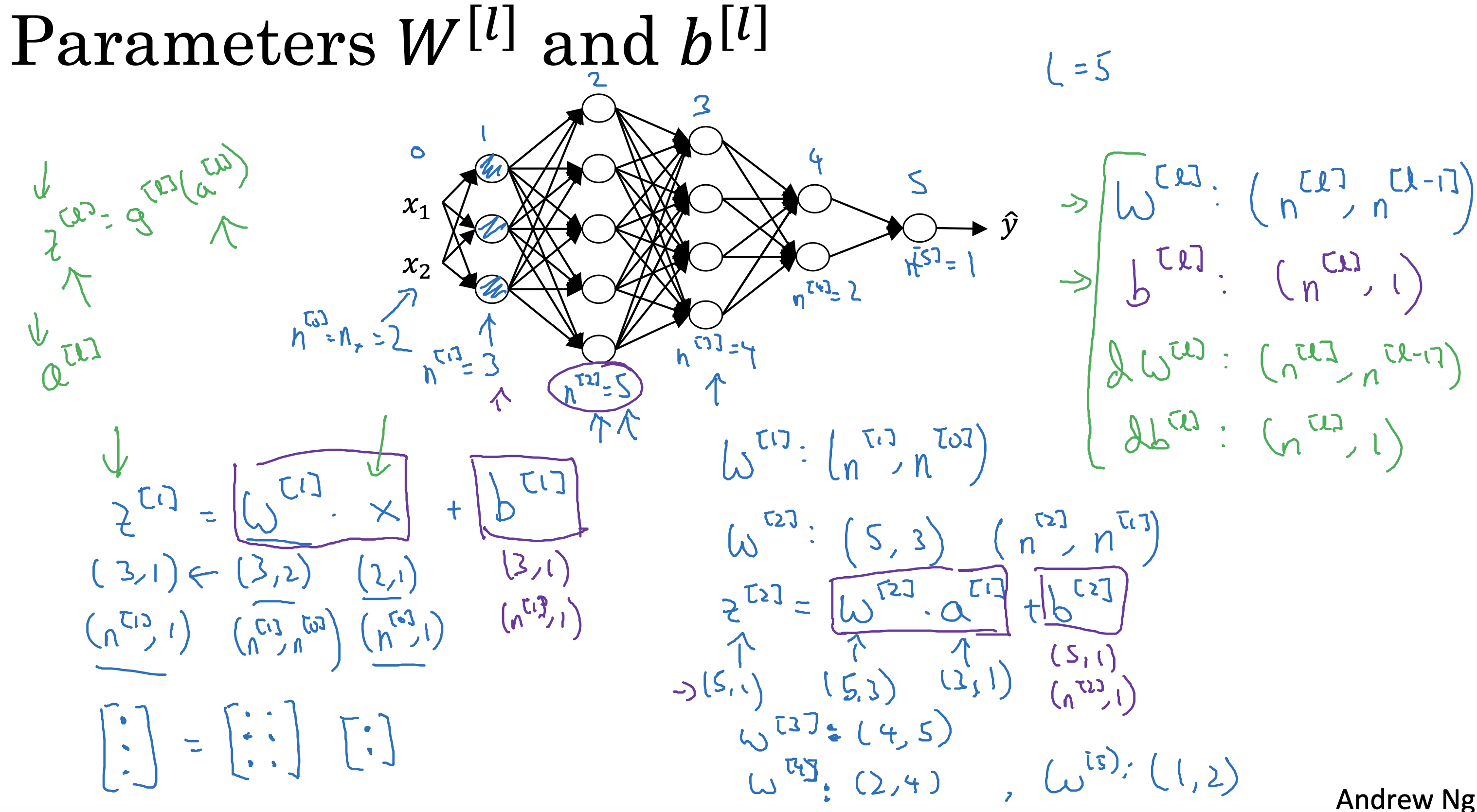
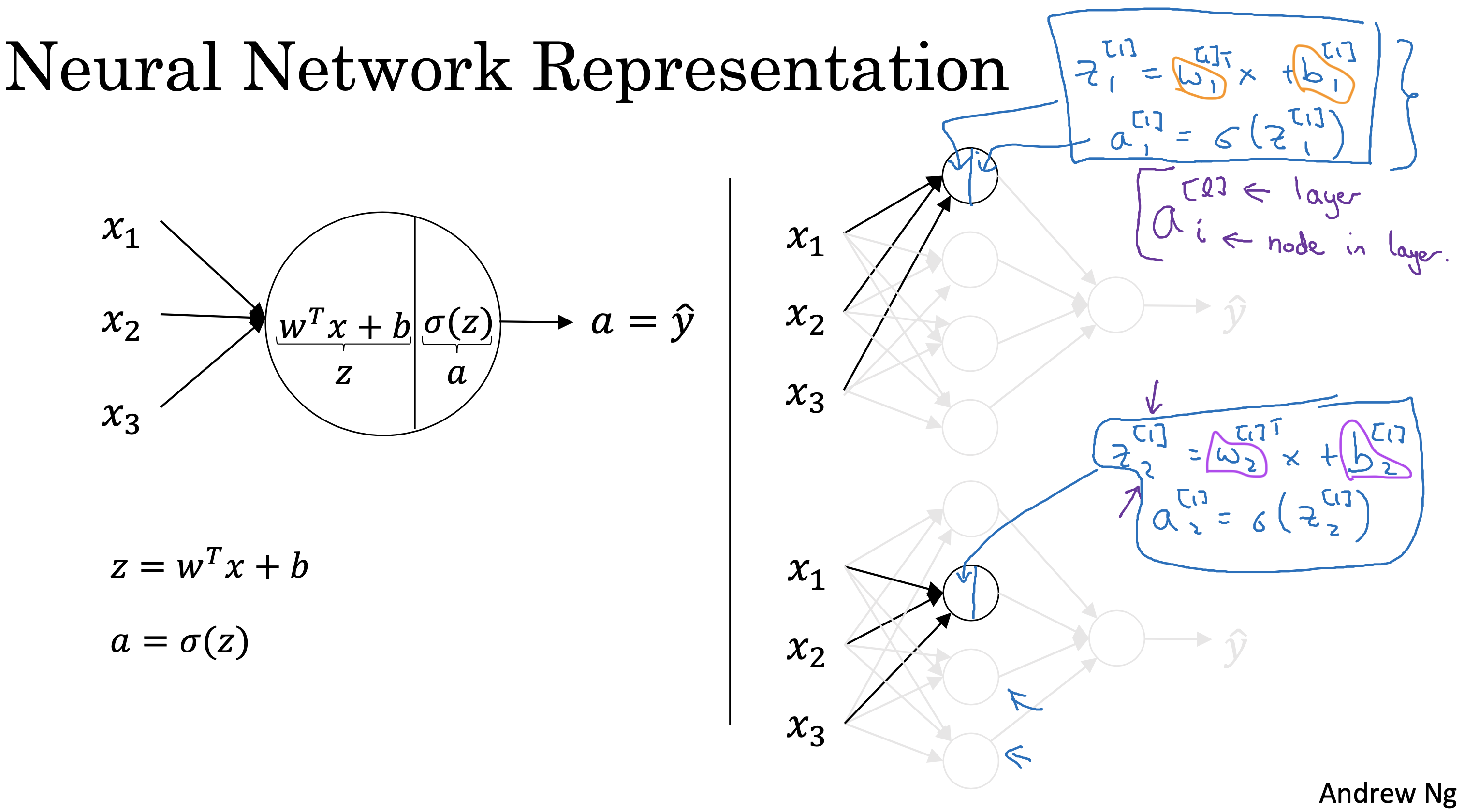
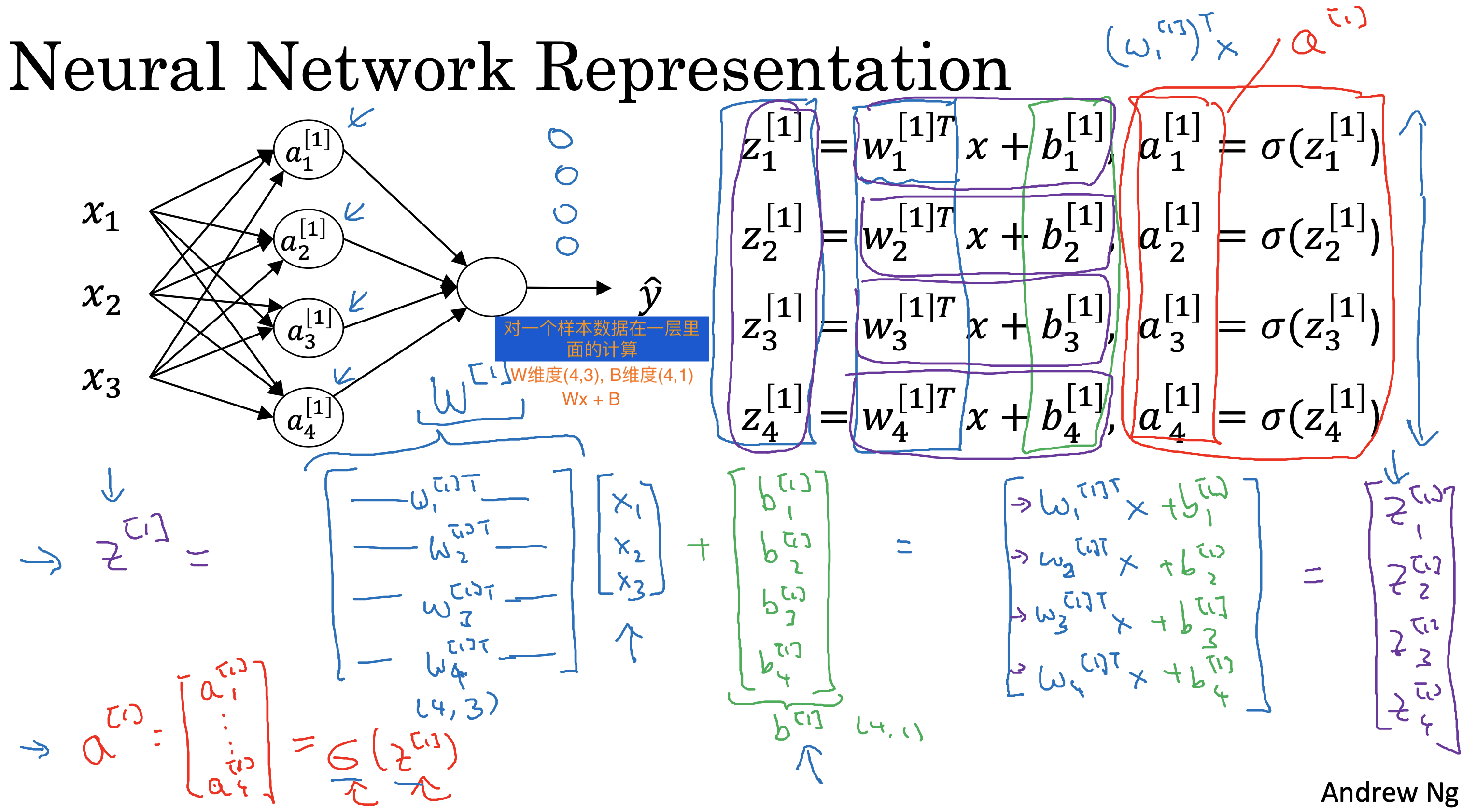
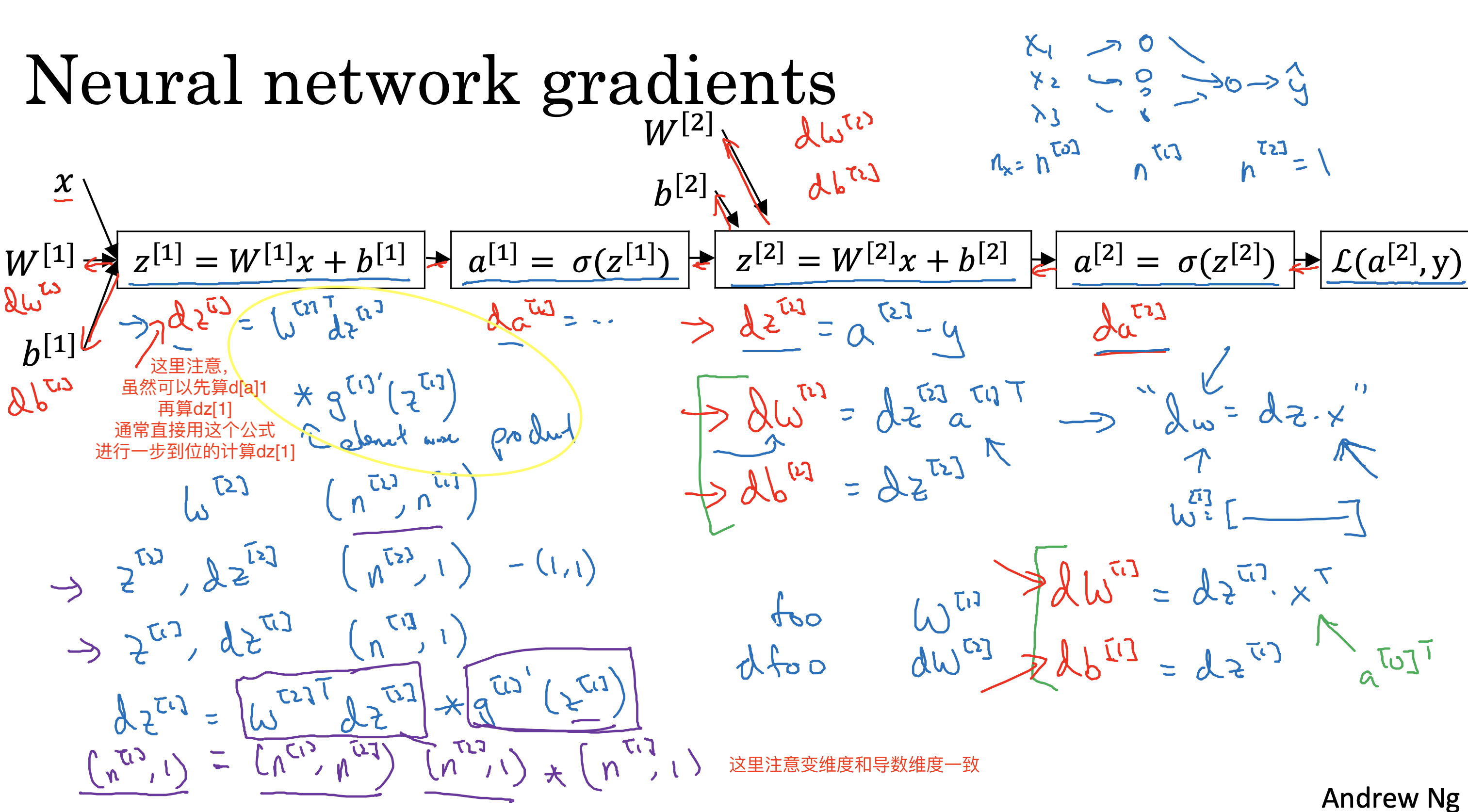
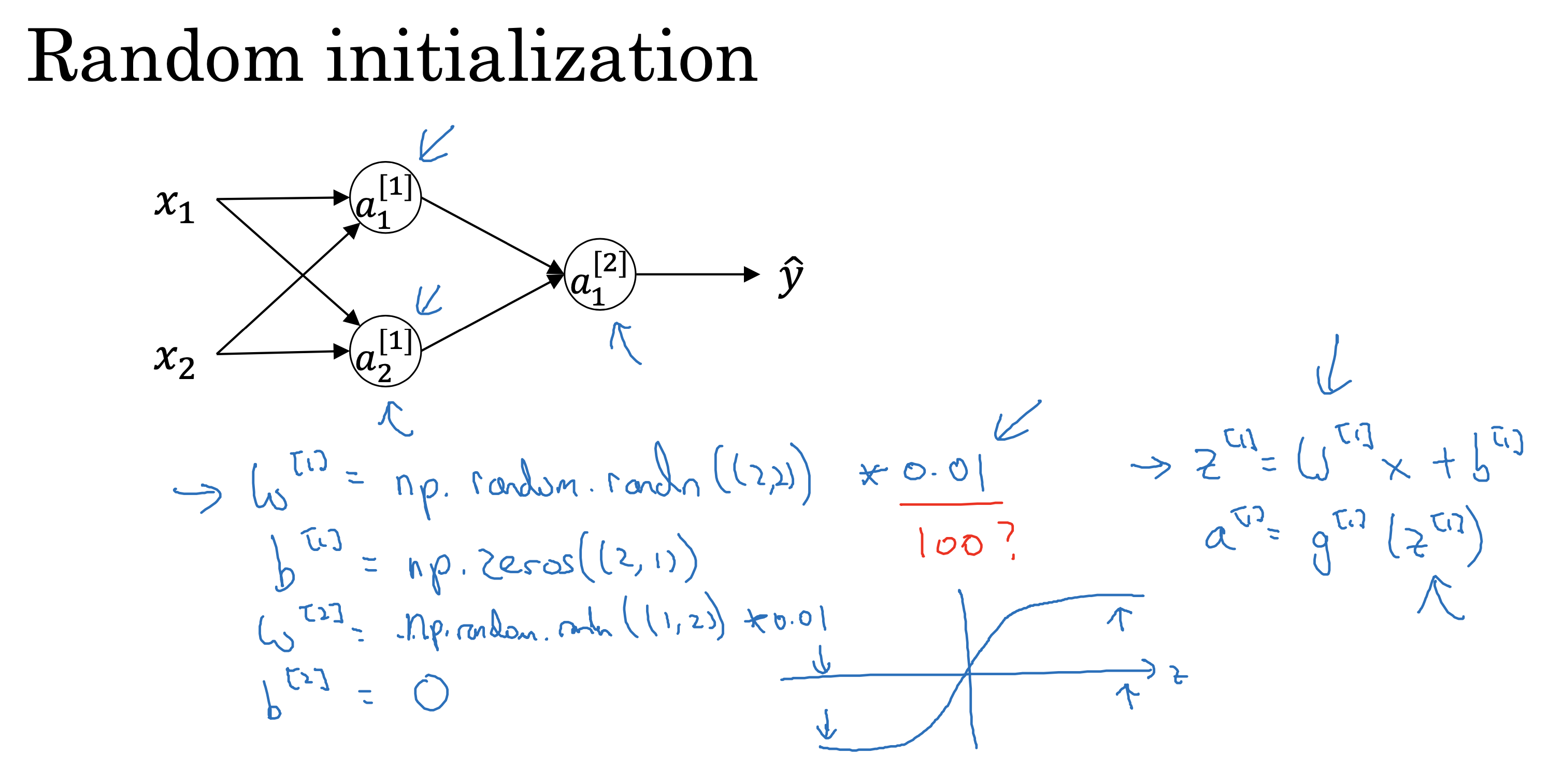
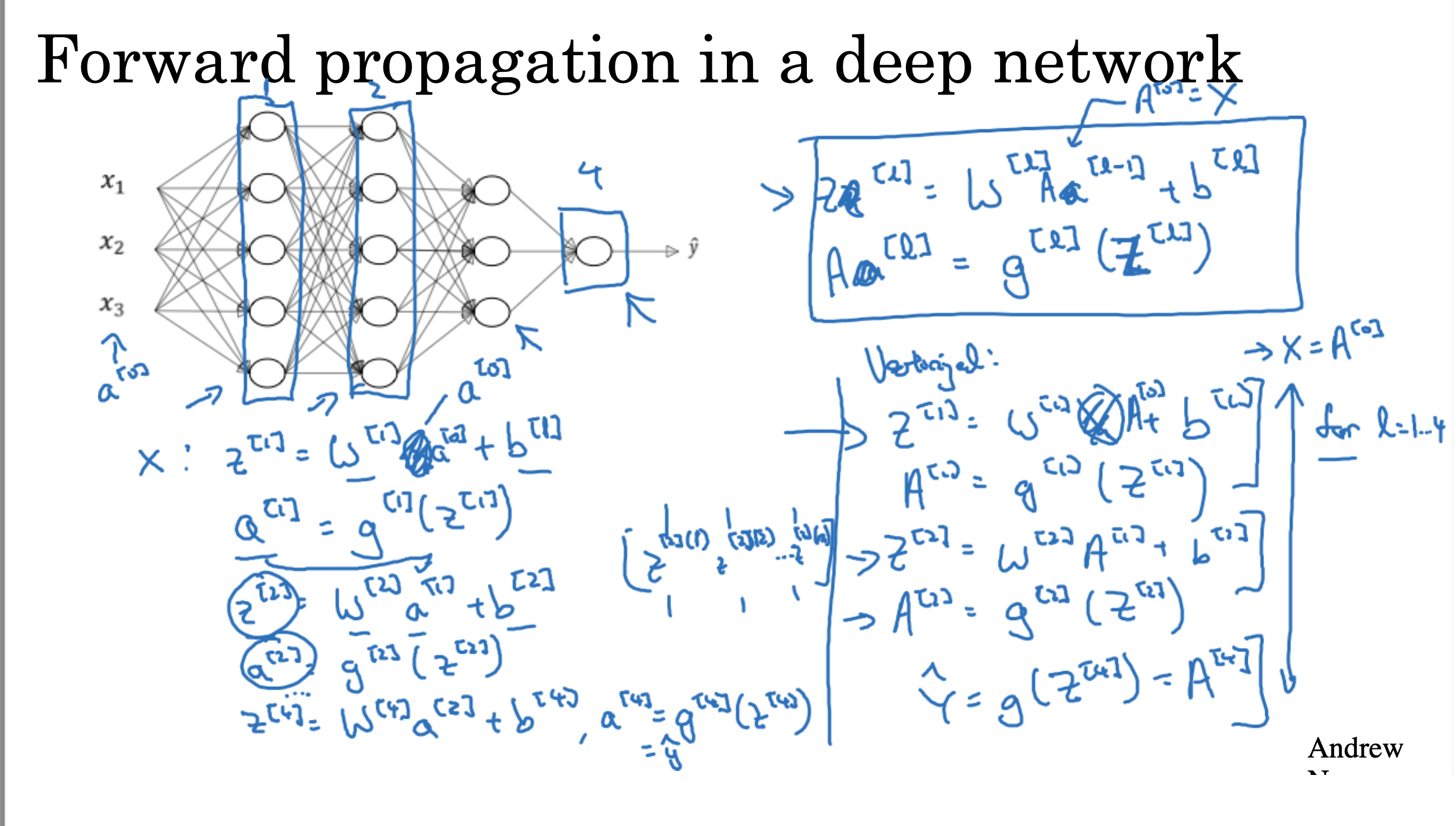
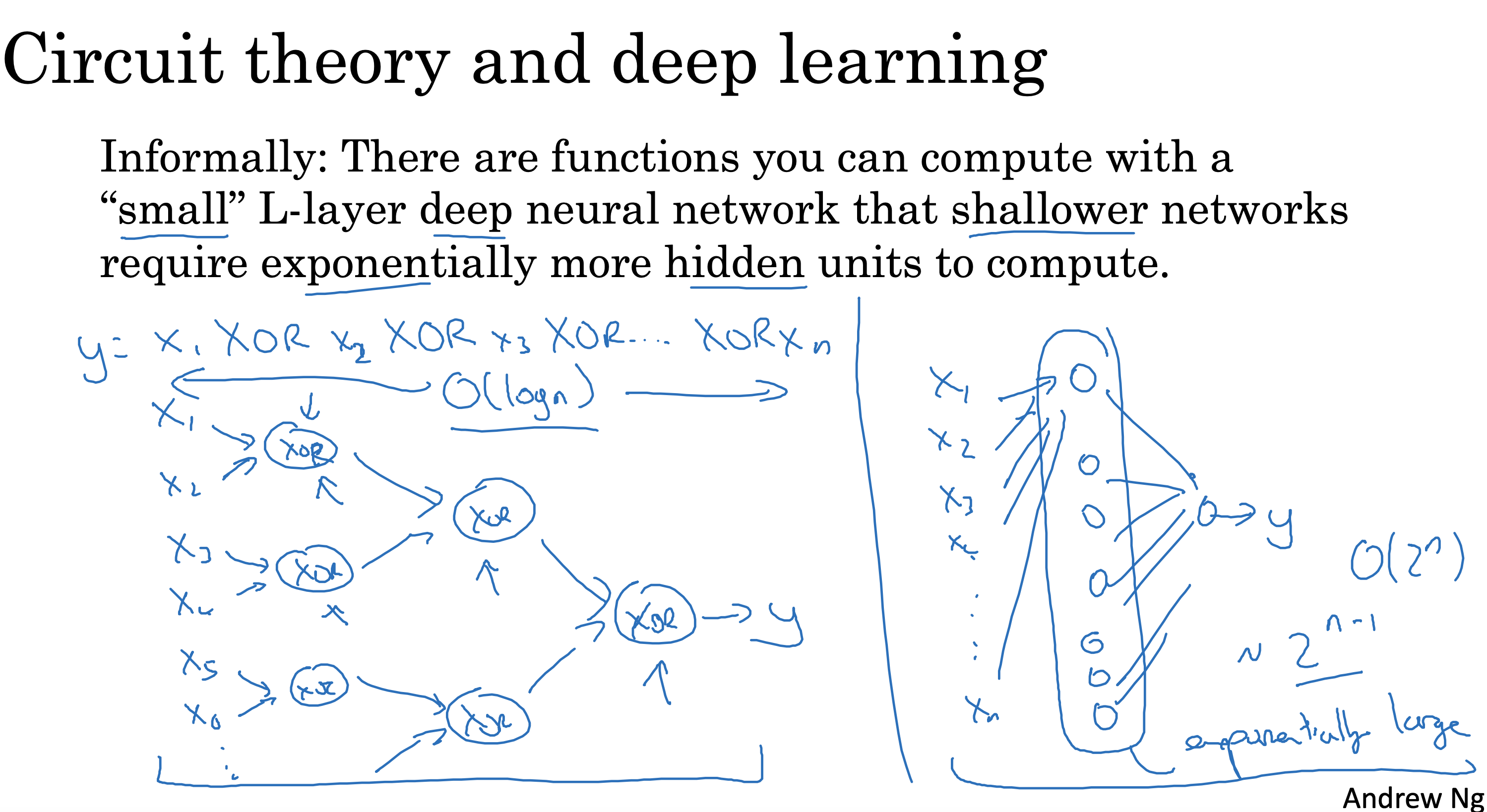
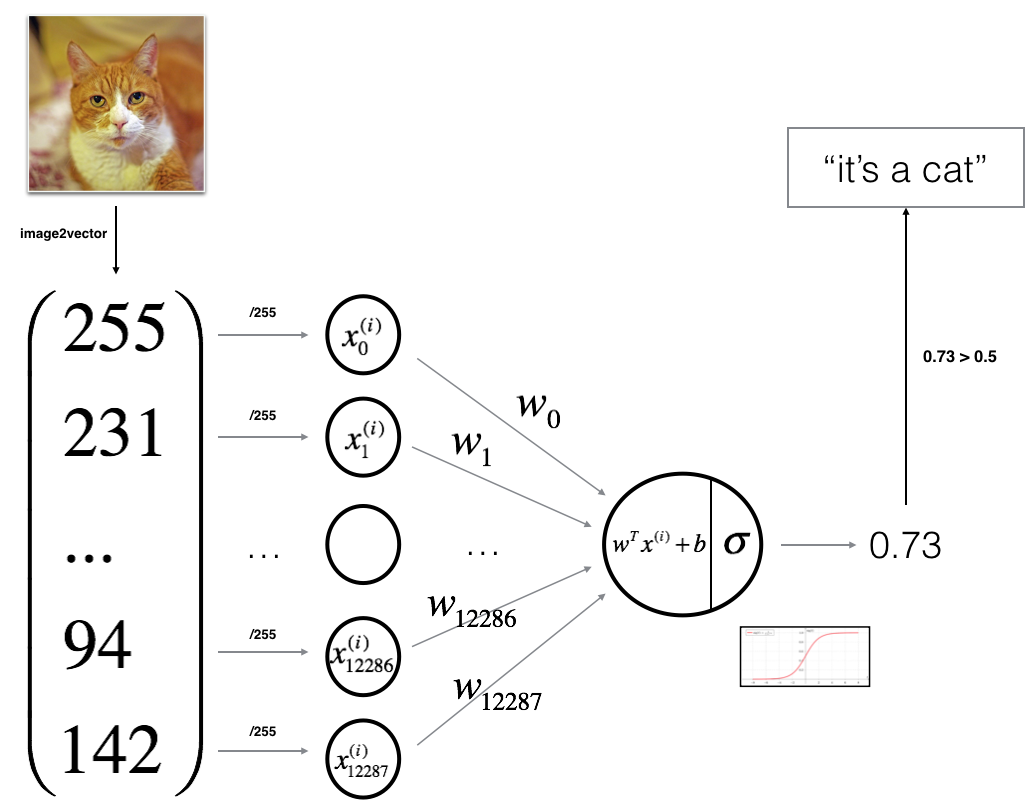
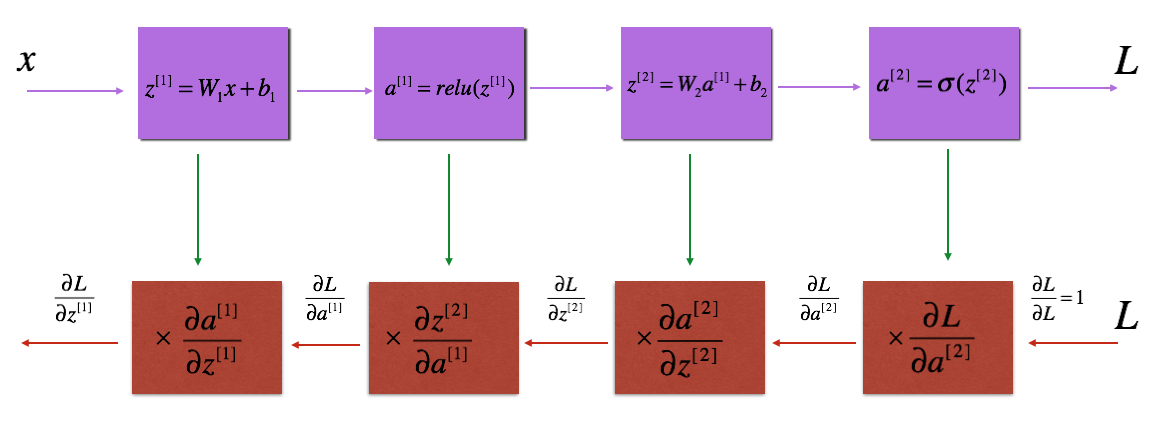
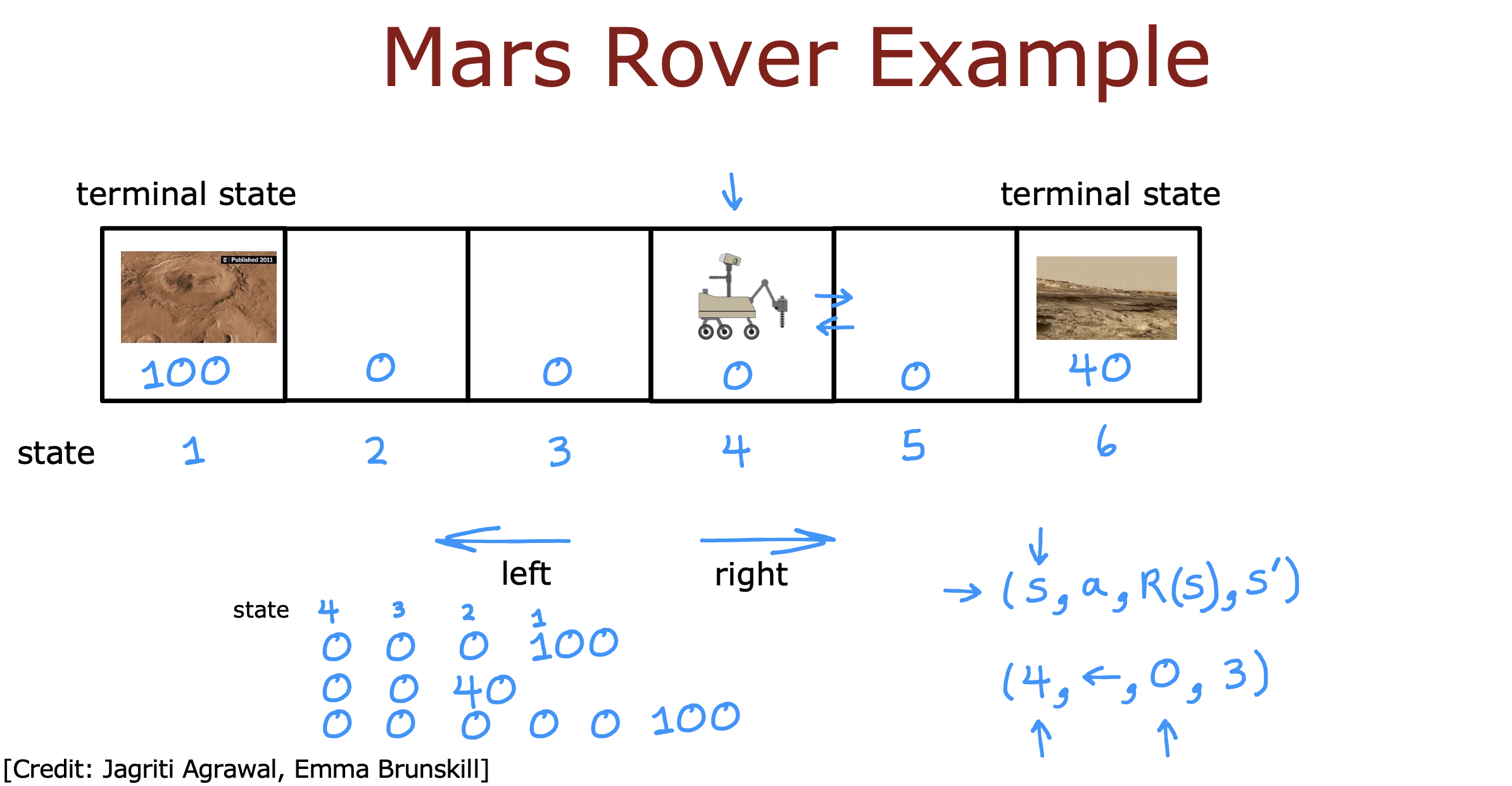
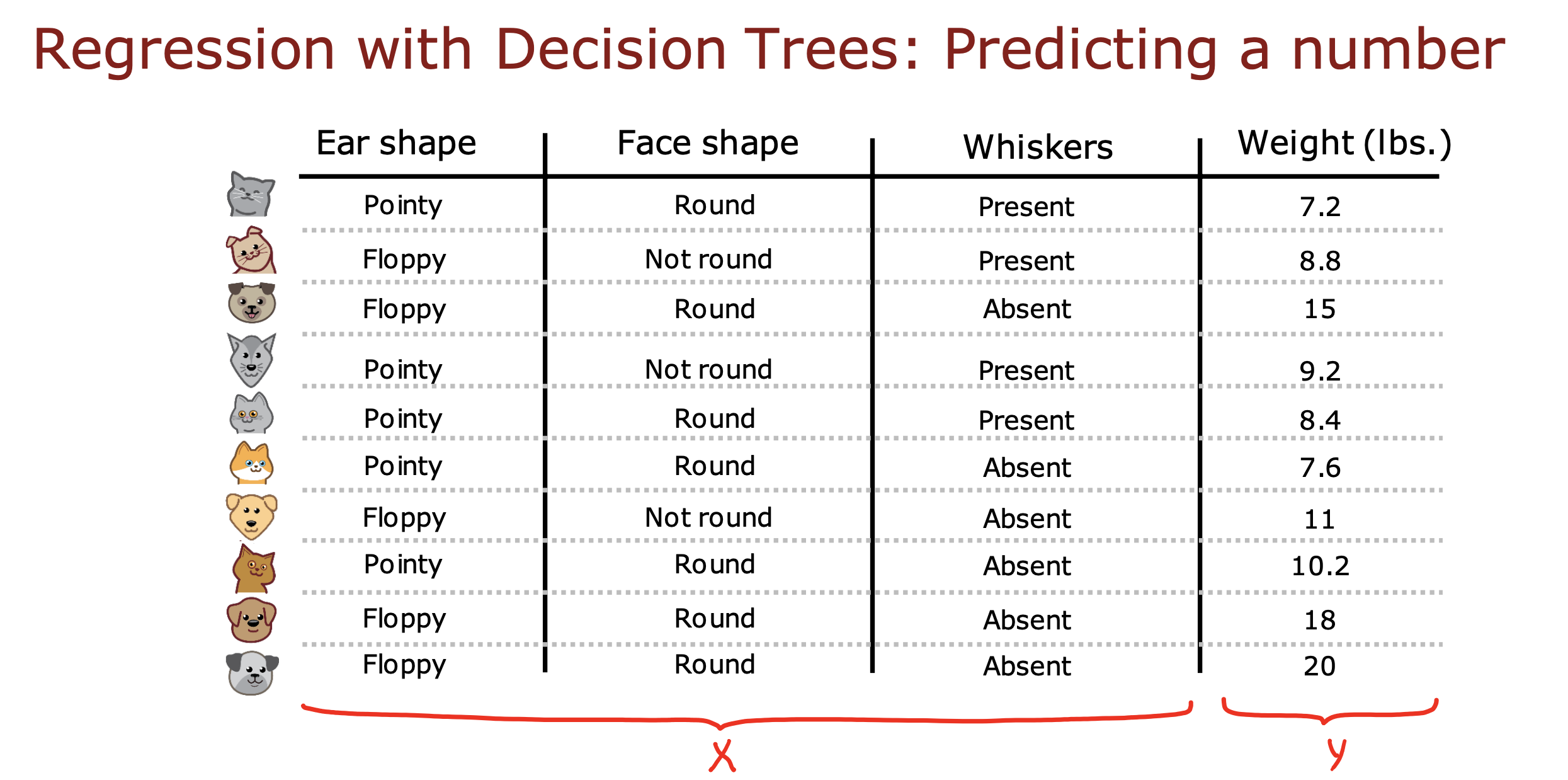
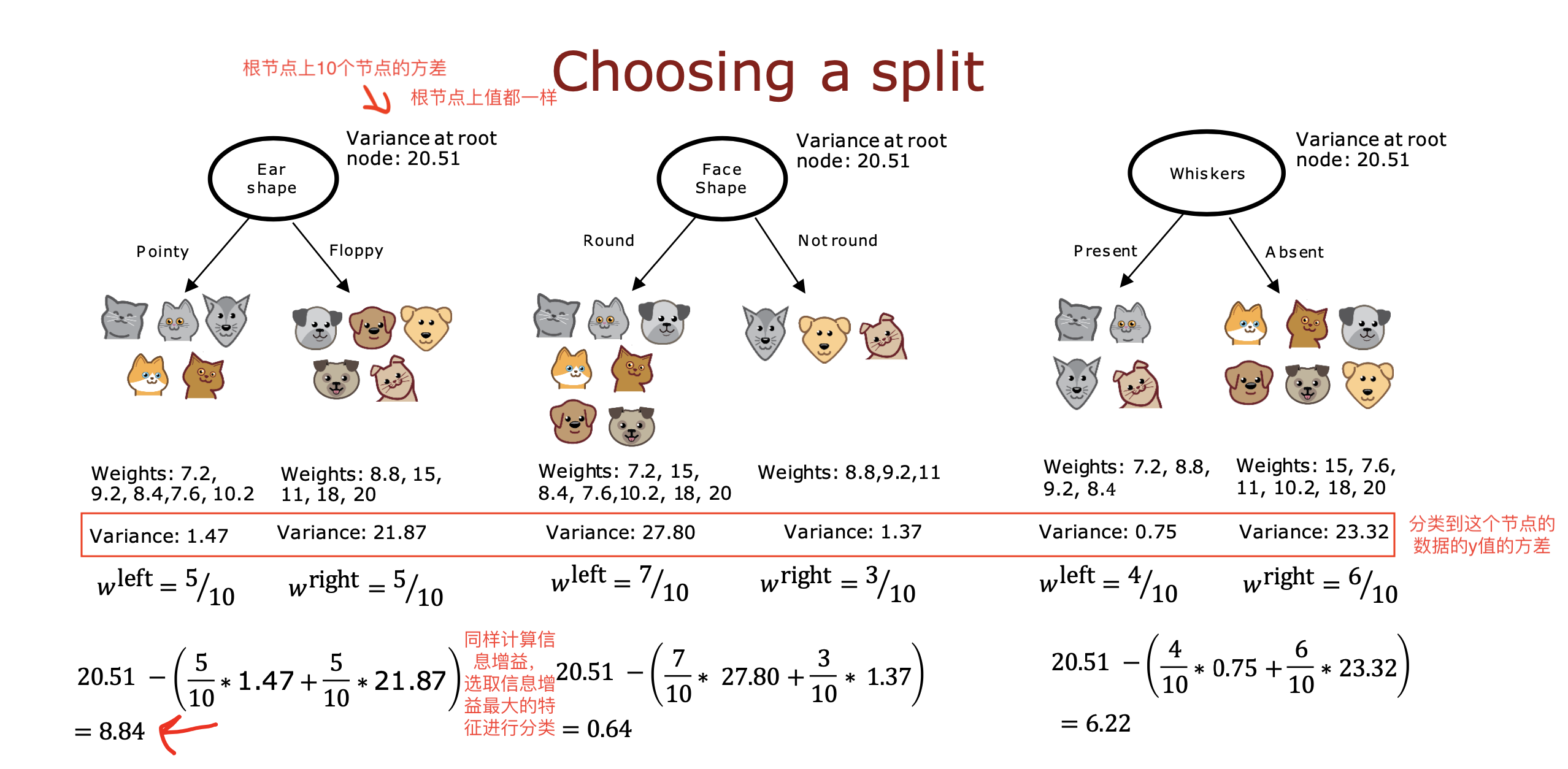
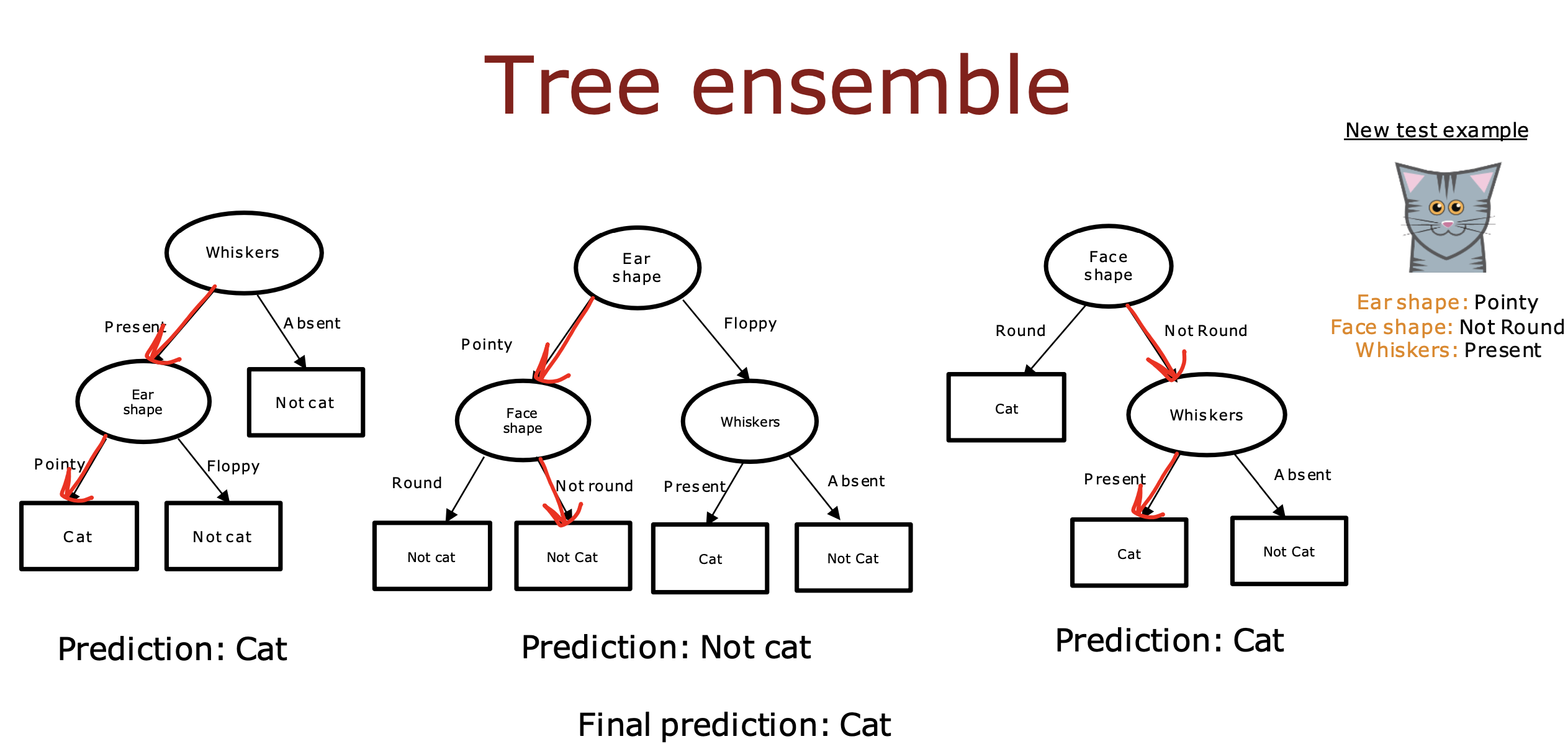
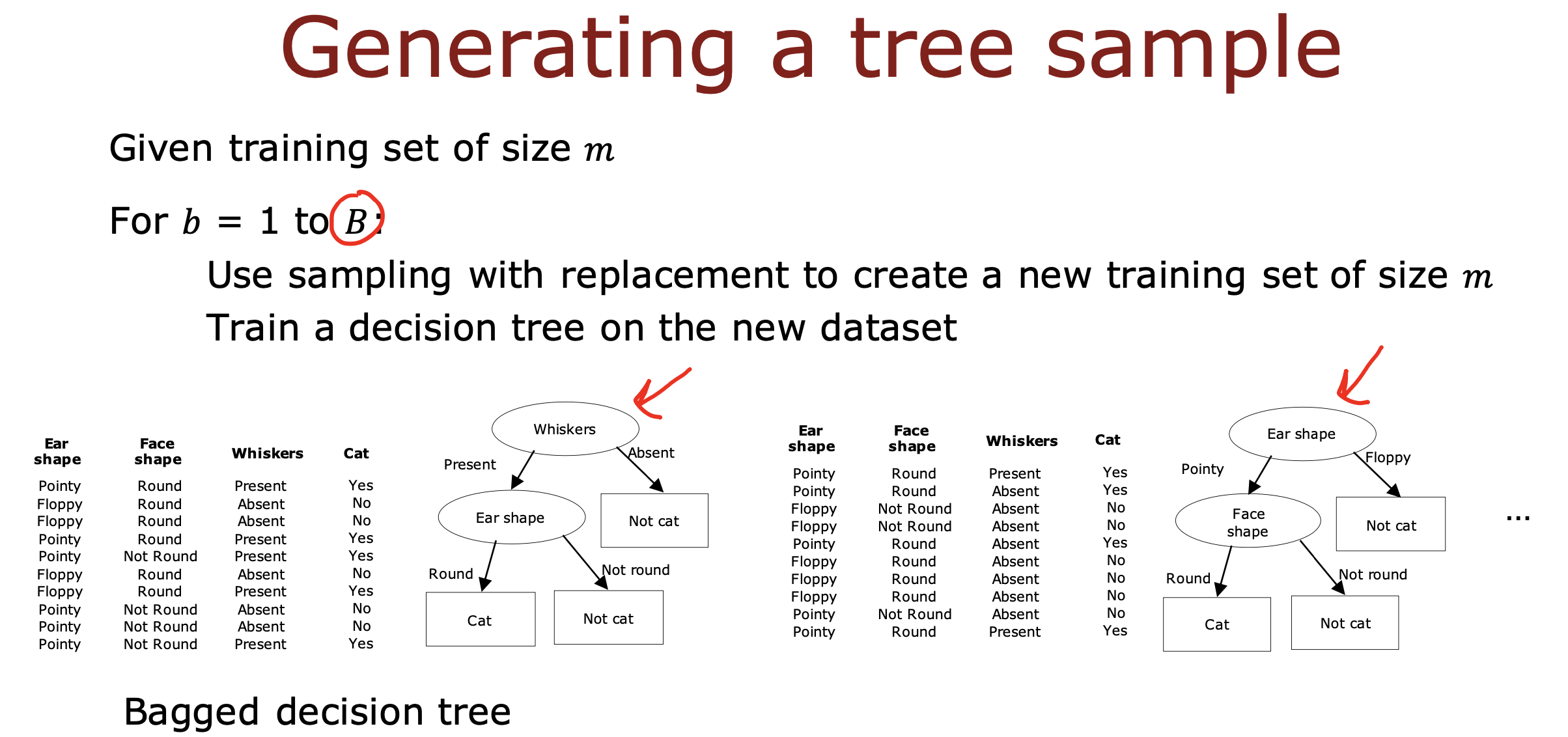
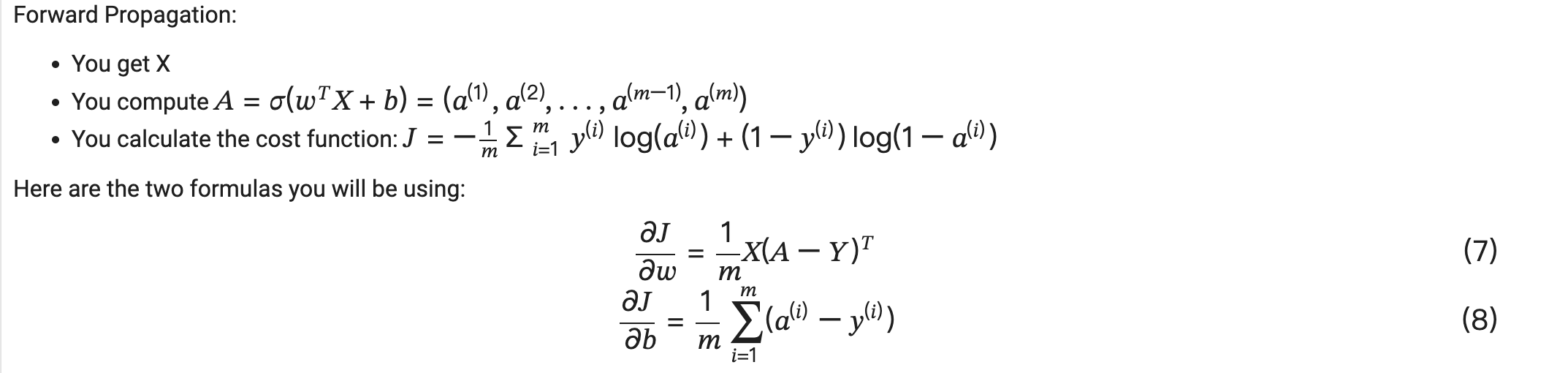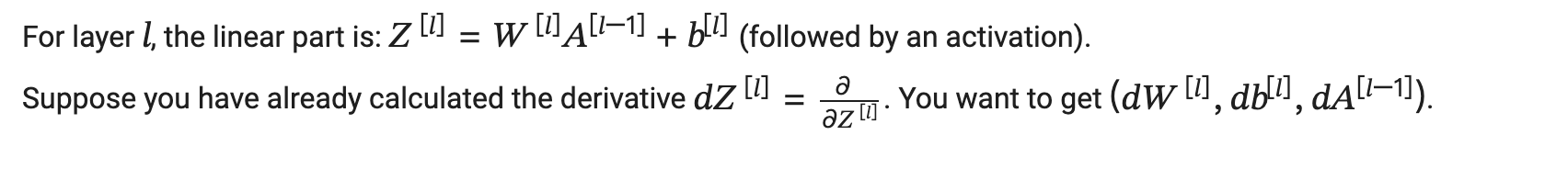背景
前端包括node层和纯前端层,需要请求第三方http接口在页面实现chatGTP的打字机效果
方案
- 在node层调用第三方http接口,避免跨域问题
- 由于第三方接口为流式接口,从node层发出请求再转发到前端也需要进行流式通信
- 前端层对返回的流式数据进行处理后更新数据呈现在页面上
实现
- 前端层使用fetch进行请求,使用ReadableStream进行流式处理
- node层使用axios进行请求,使用stream进行流式处理
node层实现
1 | import axios from 'axios'; |
前端层实现
1 | import { useState, useCallback, useRef } from 'react'; |
番外: 全局节流函数
1 | const throttleTimerList: { [key: string]: Timeout | null } = {}; |
相关知识链接
NODE-Stream
NODE-ReadableStream
ReadableStream
application/octet-stream vs text/event-stream
AbortController
fetch获取流式数据相关问题
在 Koa 中基于 gpt-3.5 模型实现一个最基本的流式问答 DEMO