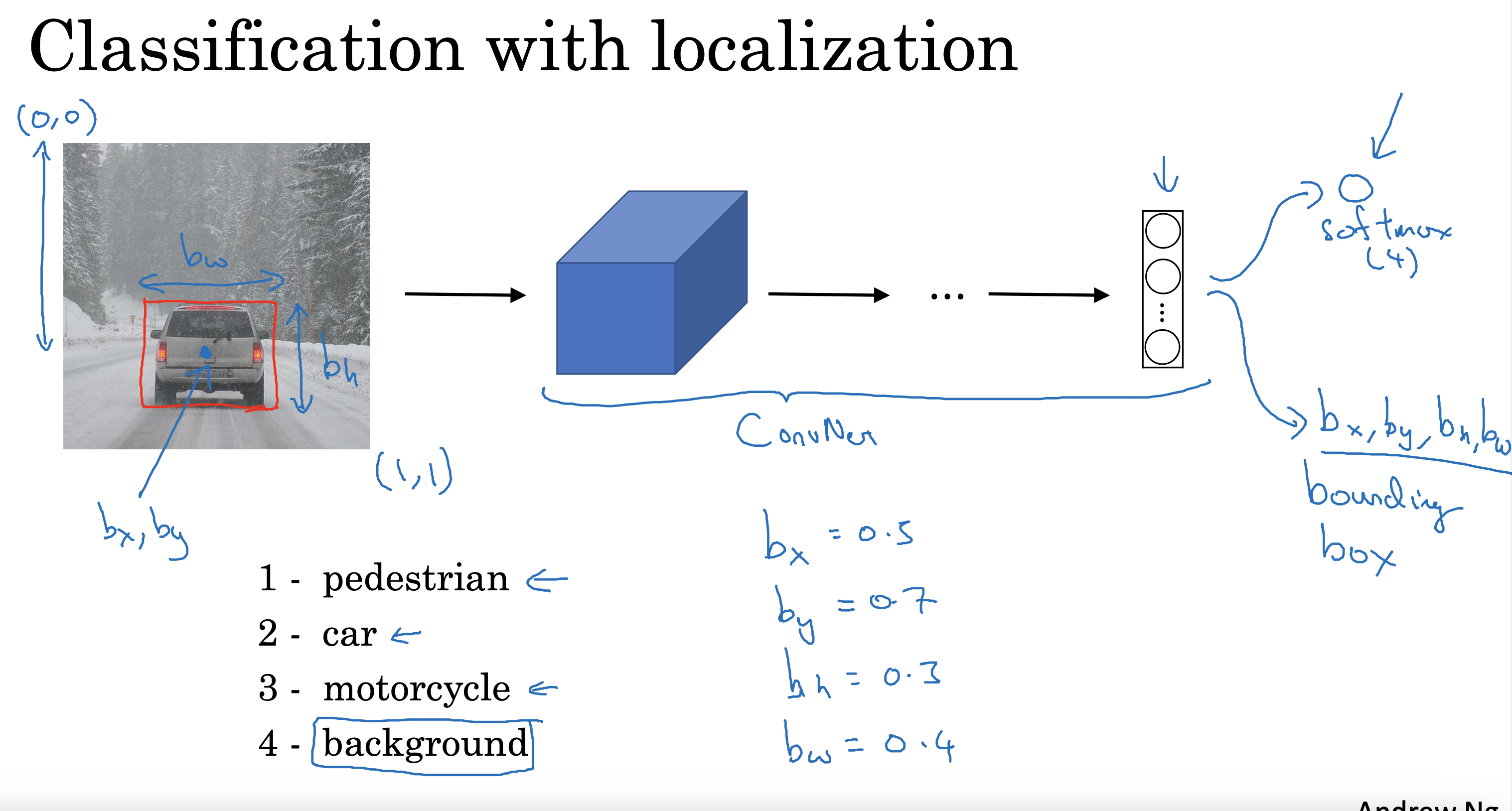
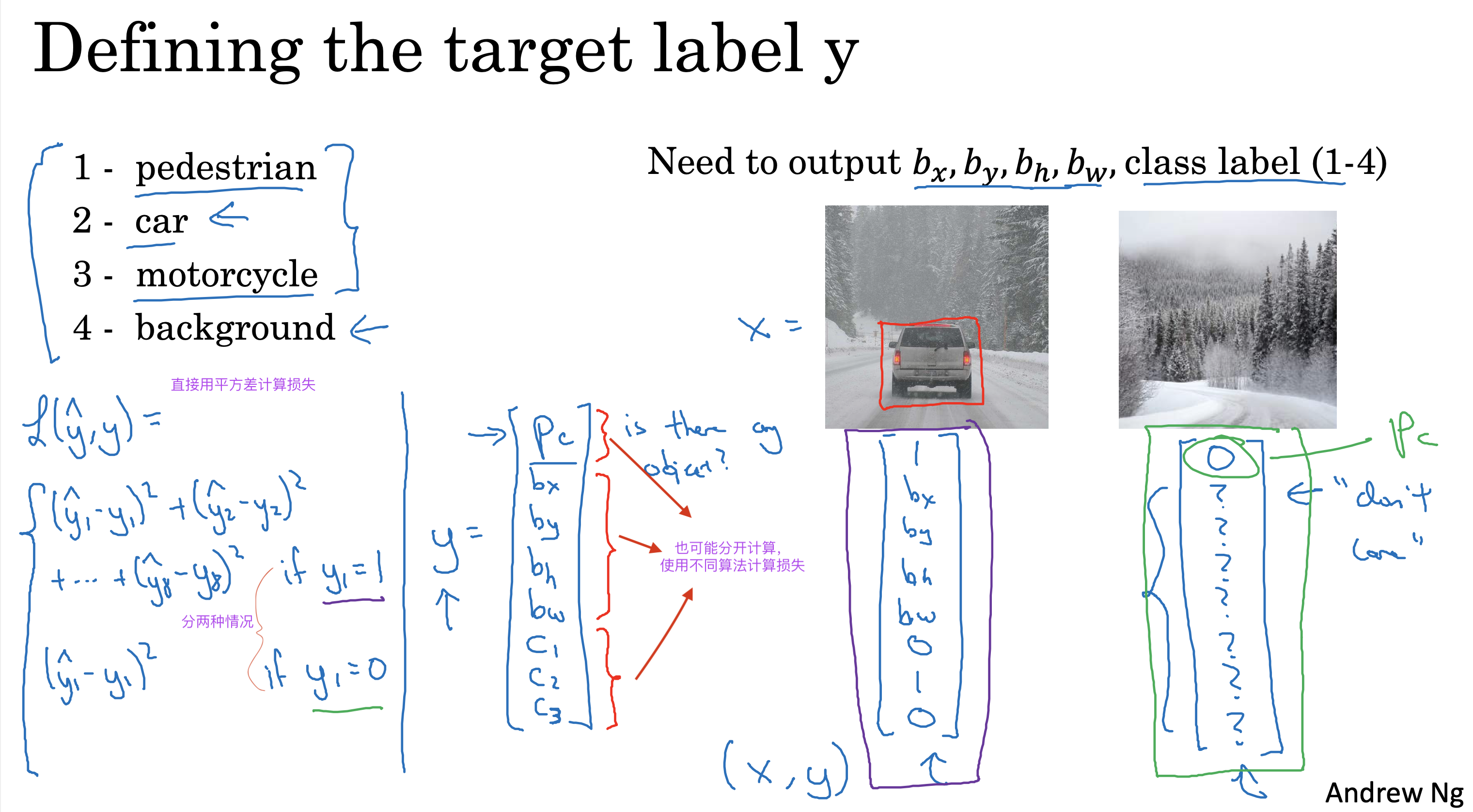
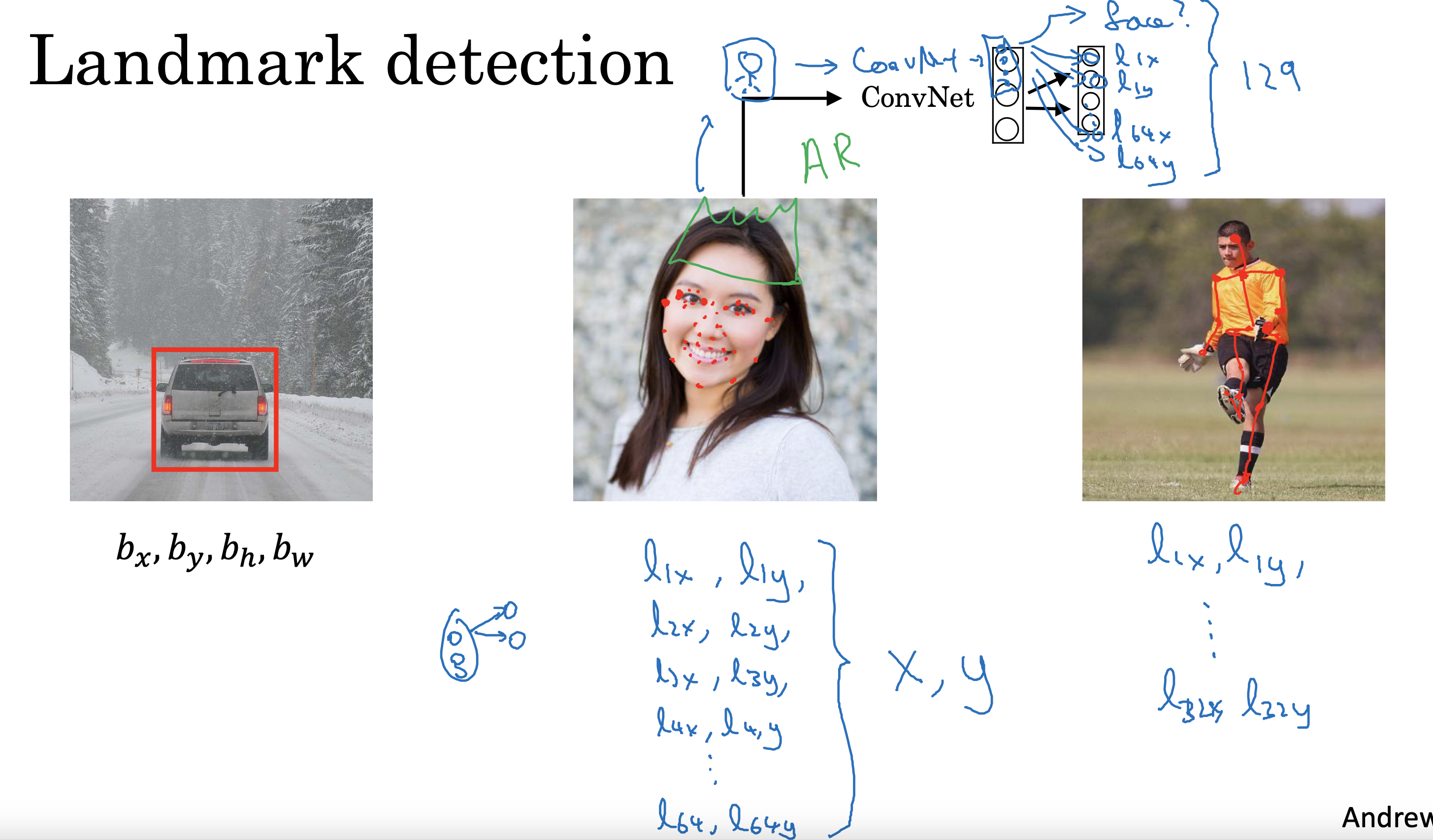
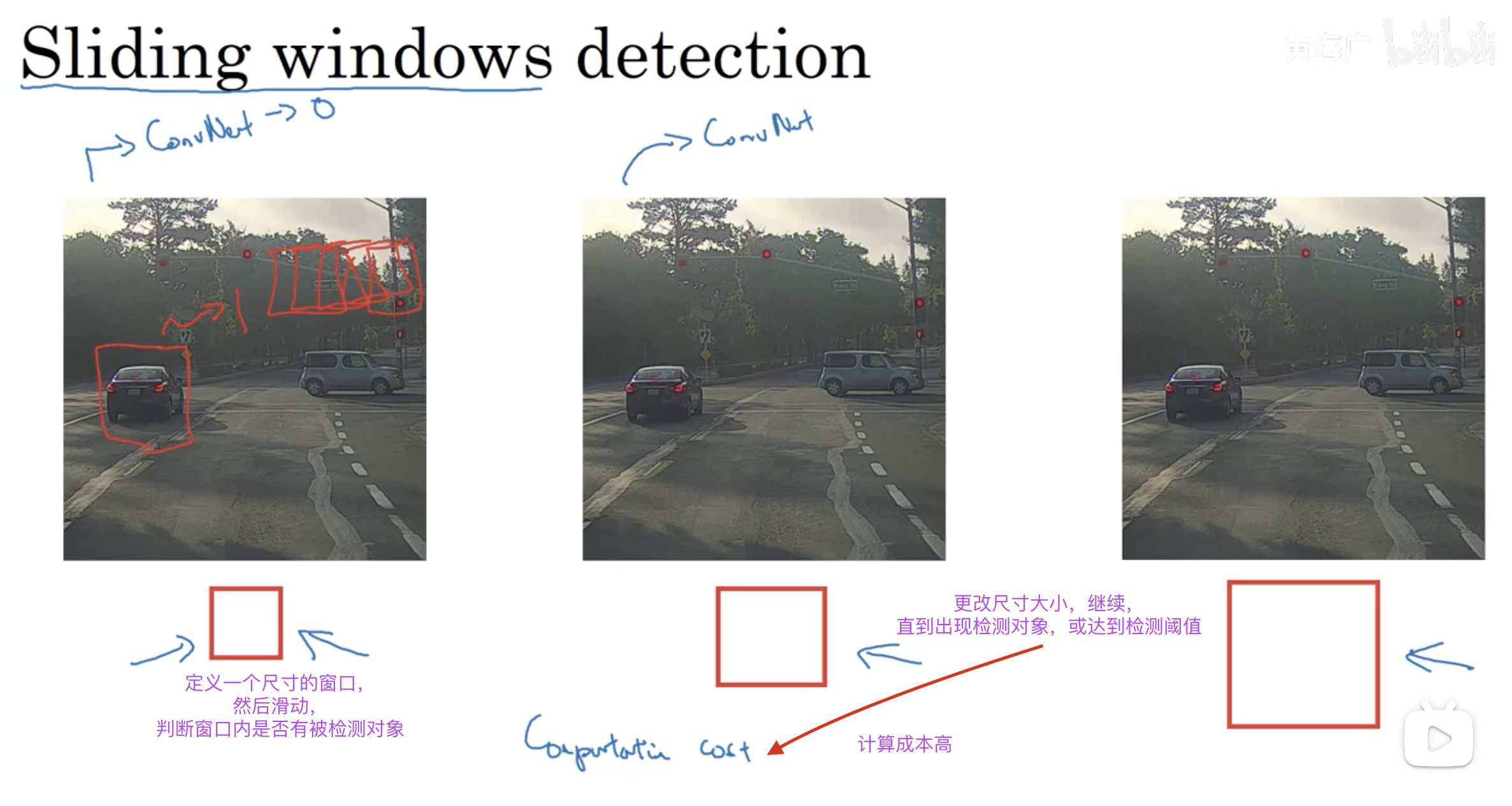
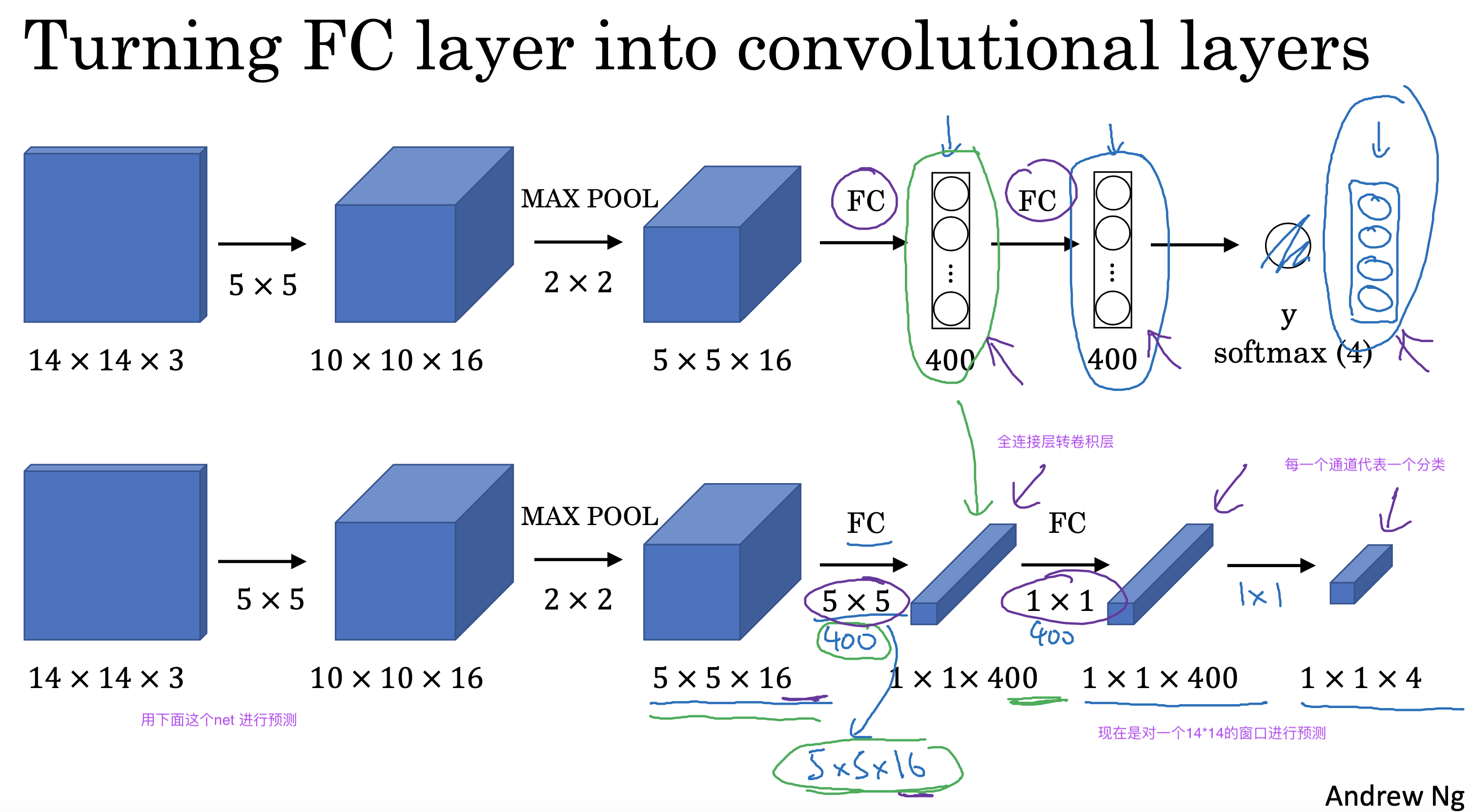
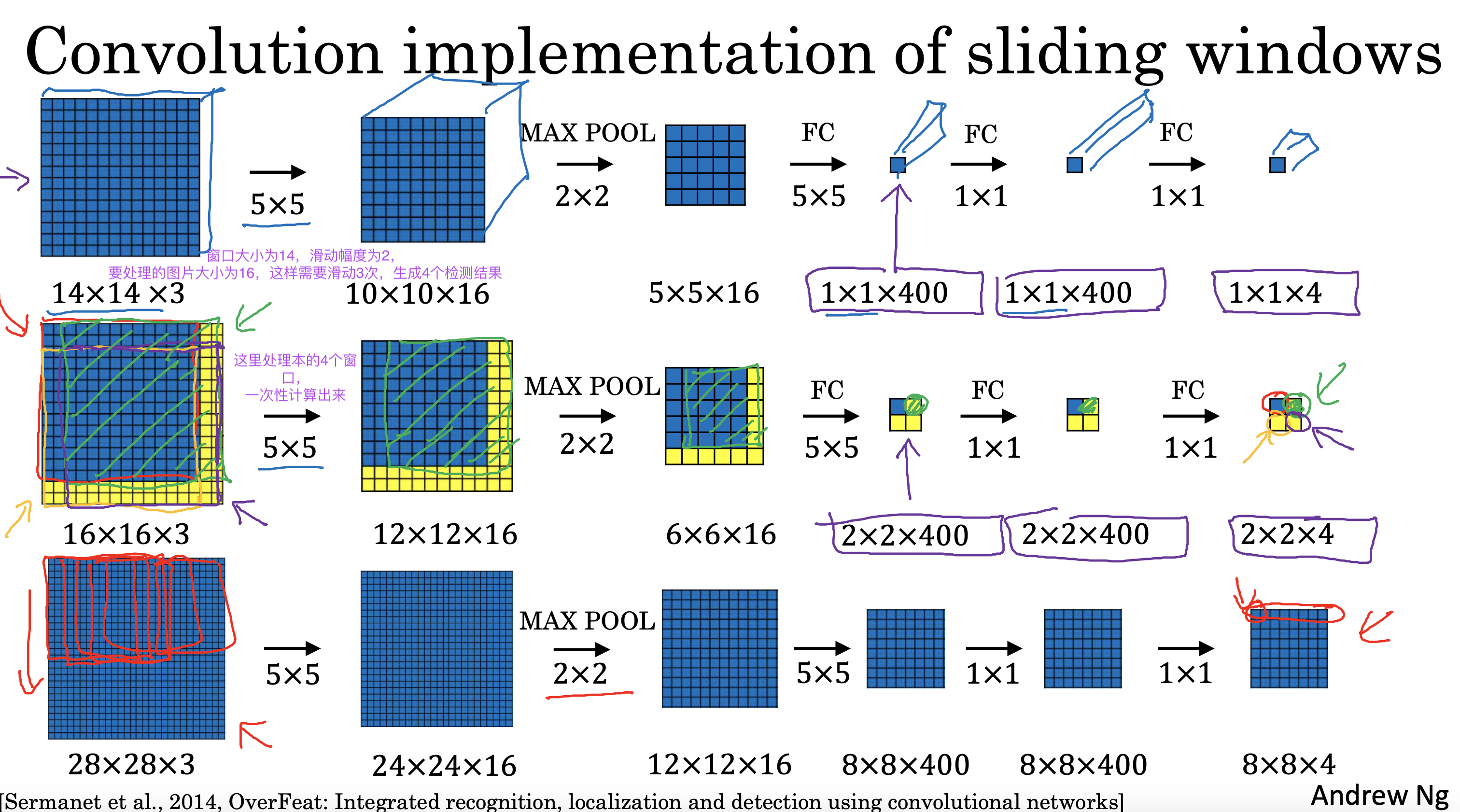
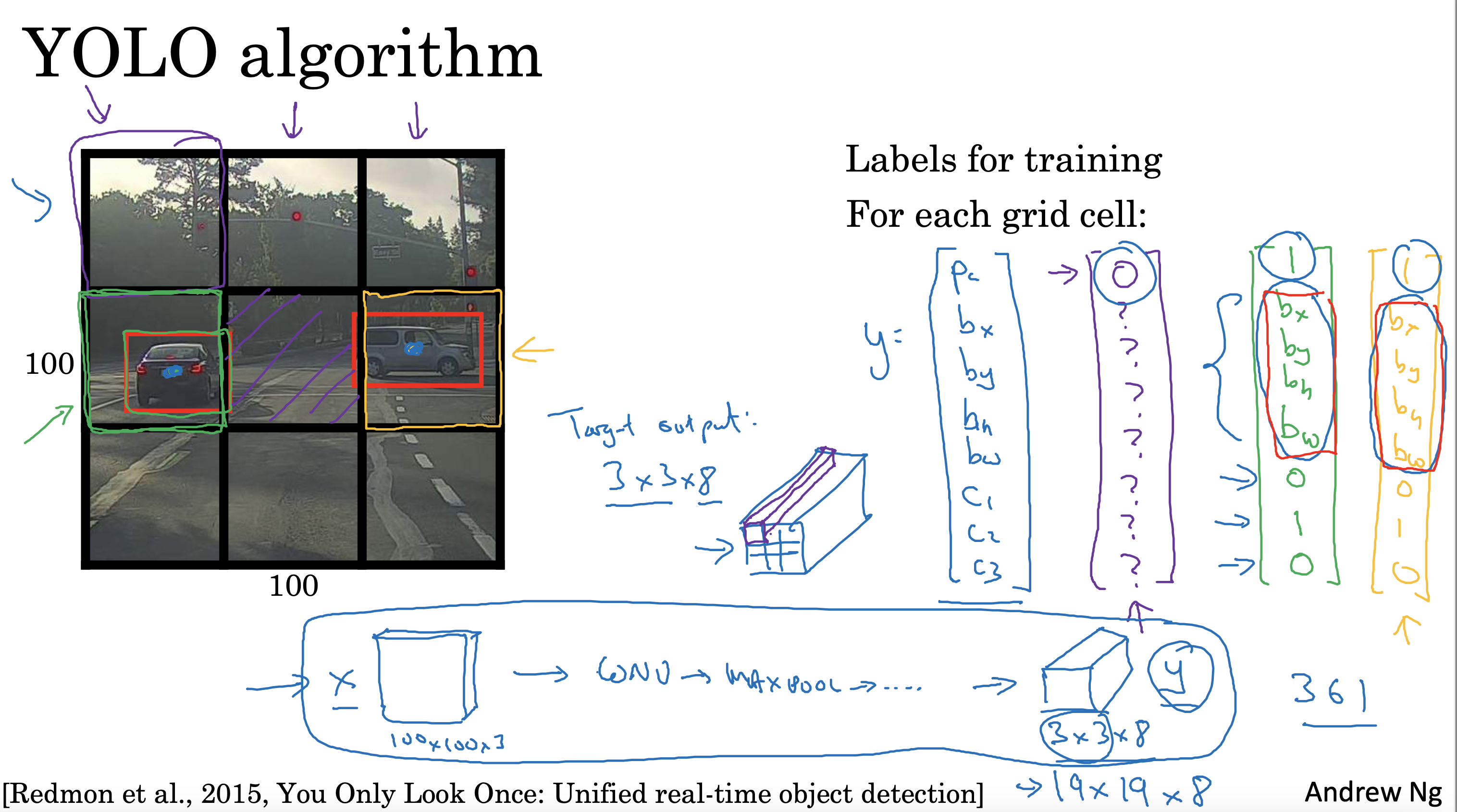
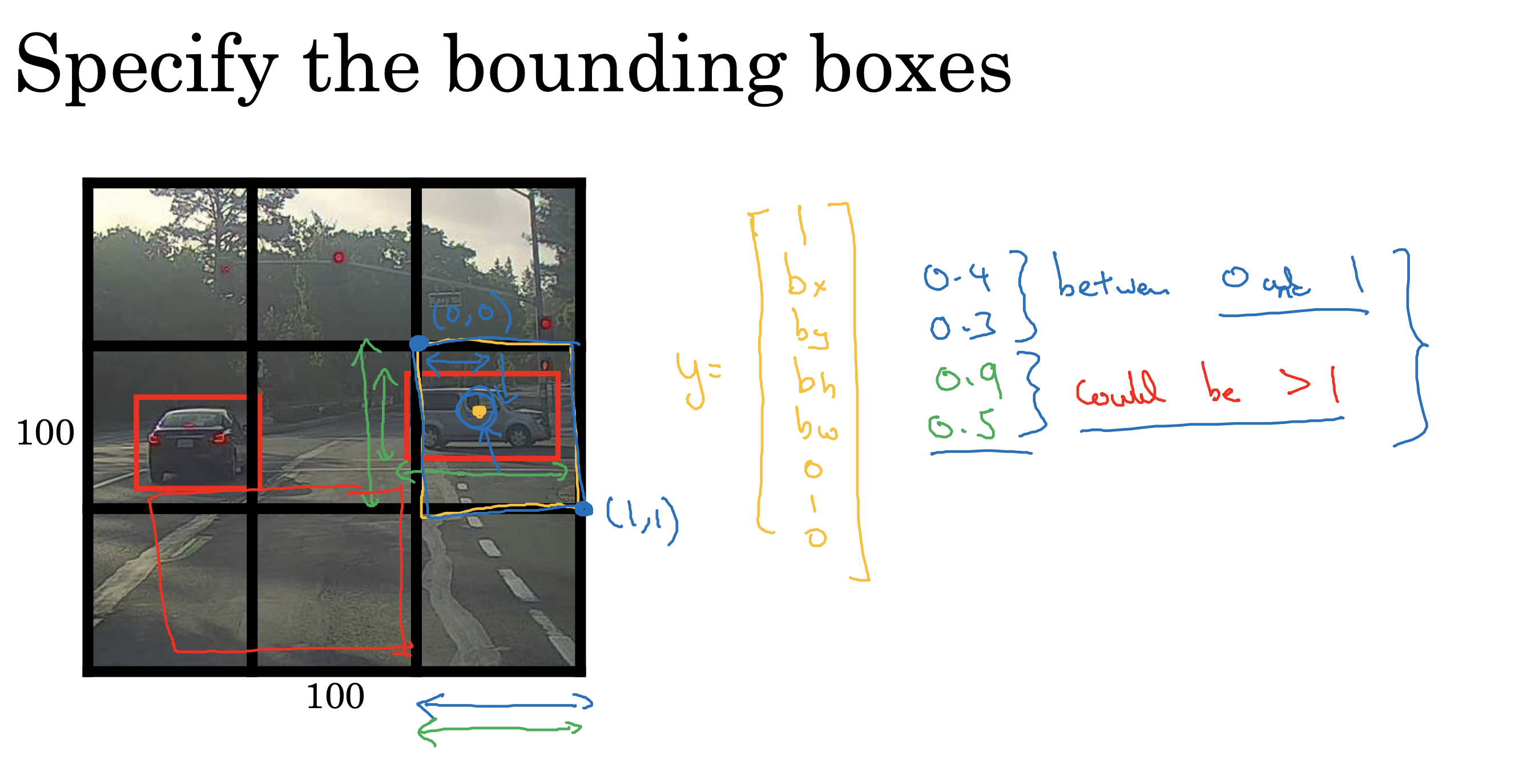
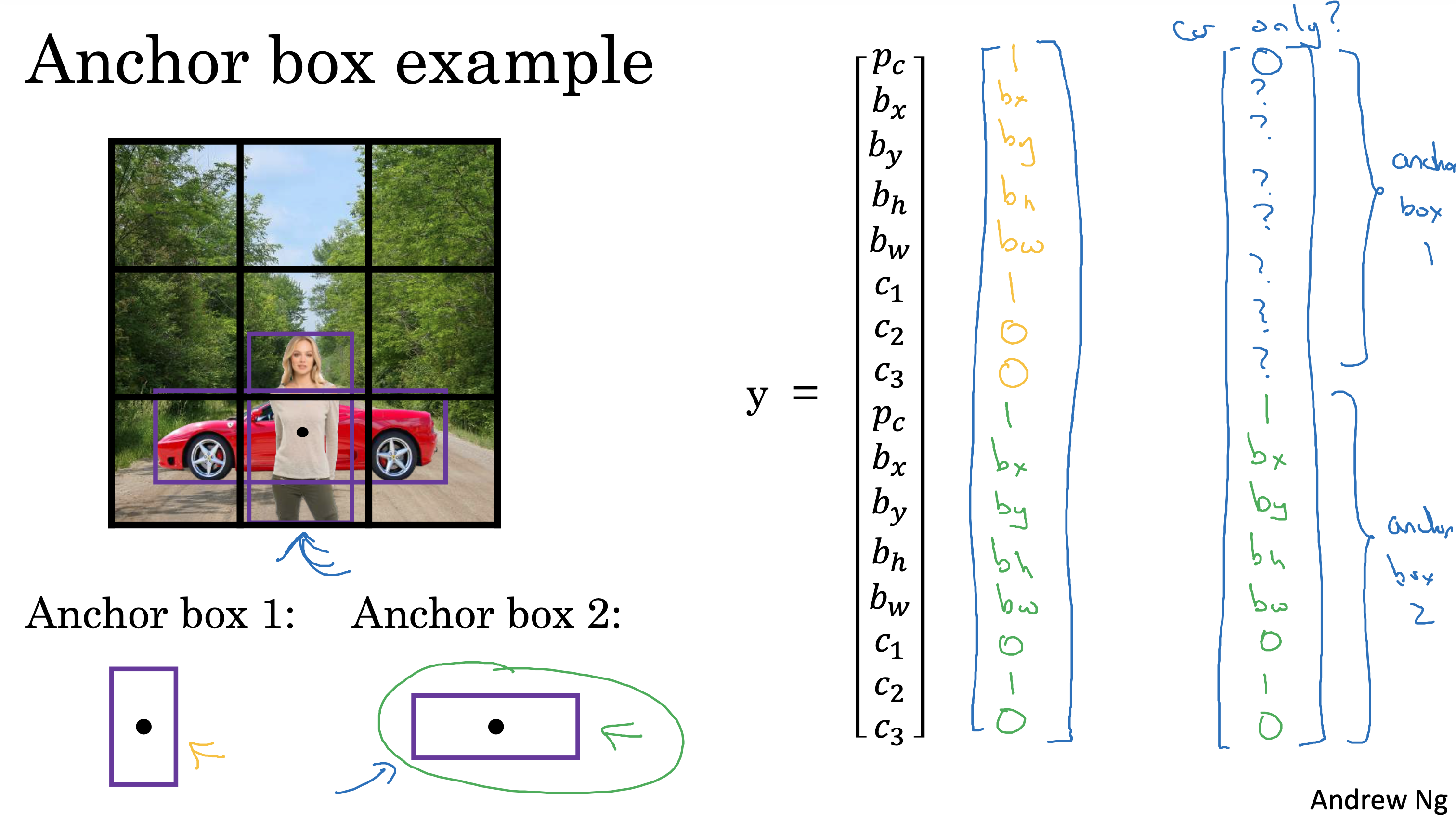
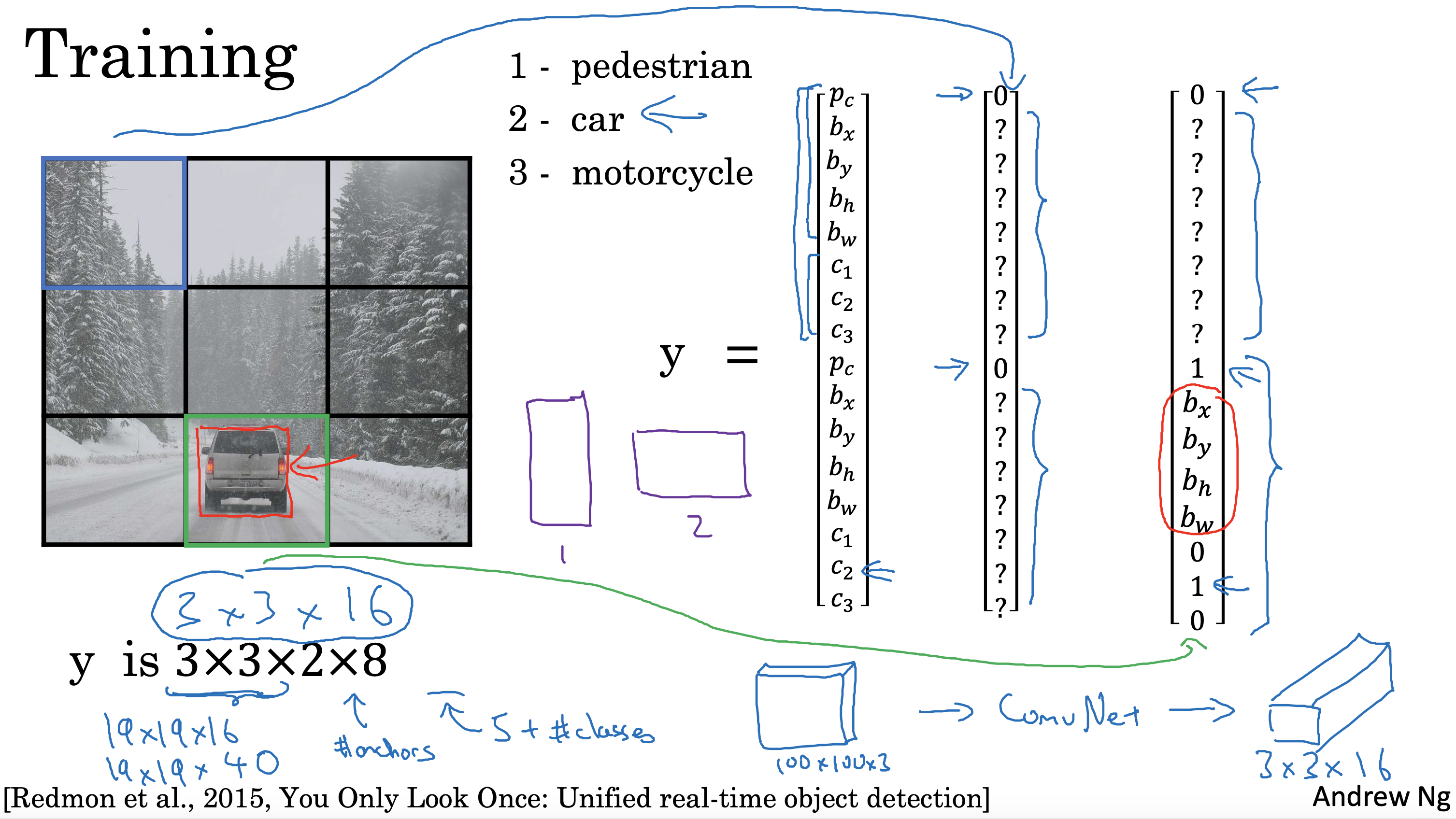
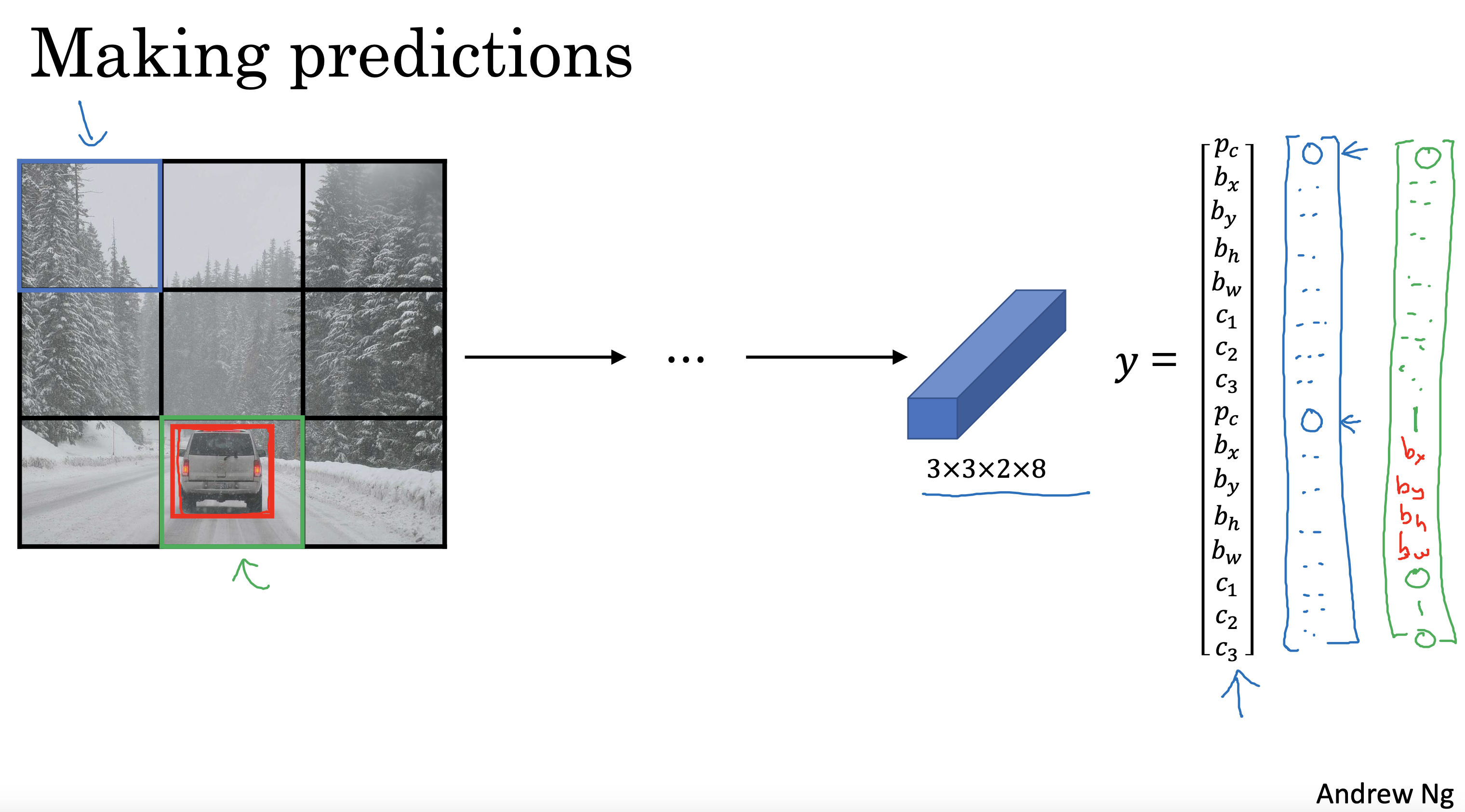
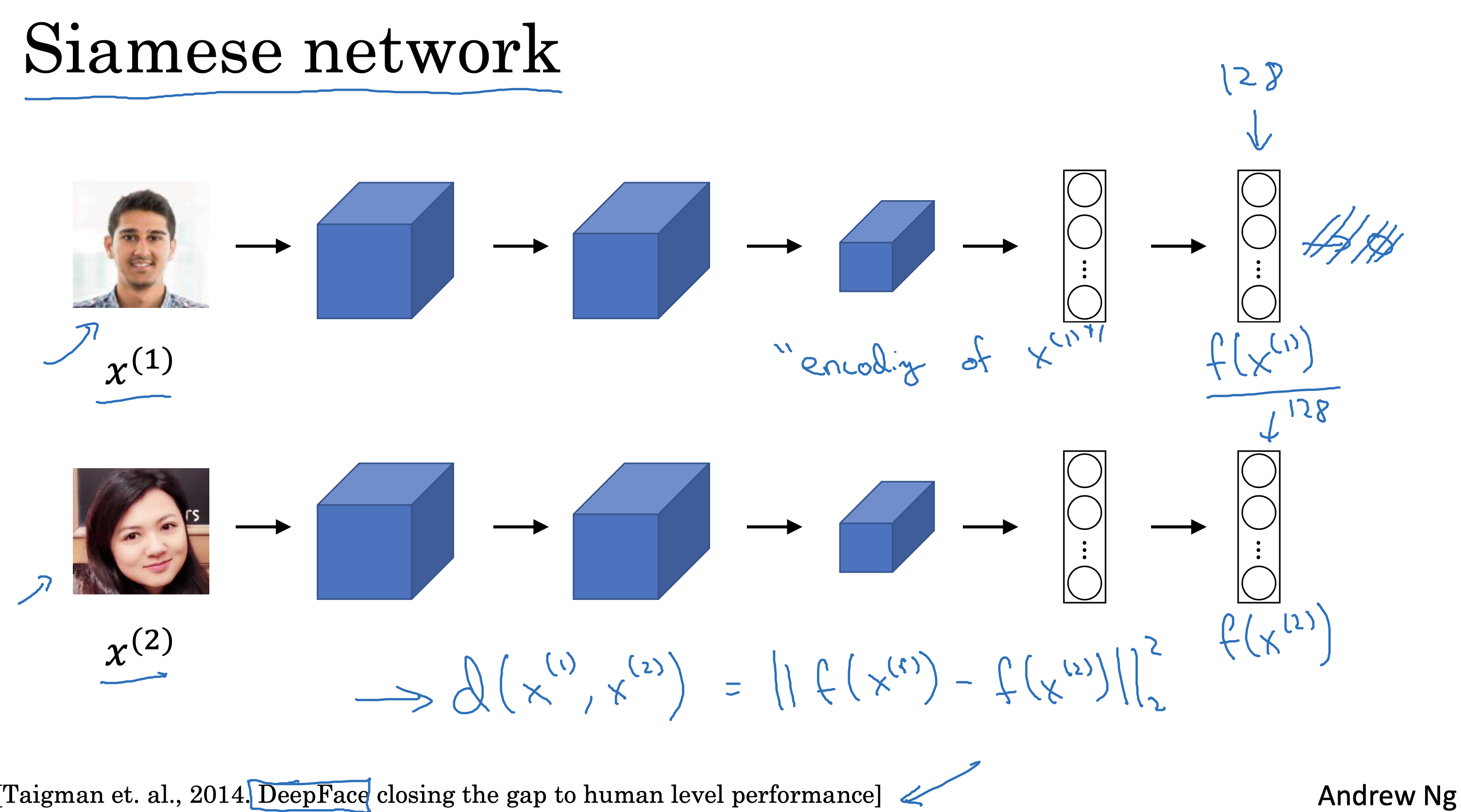
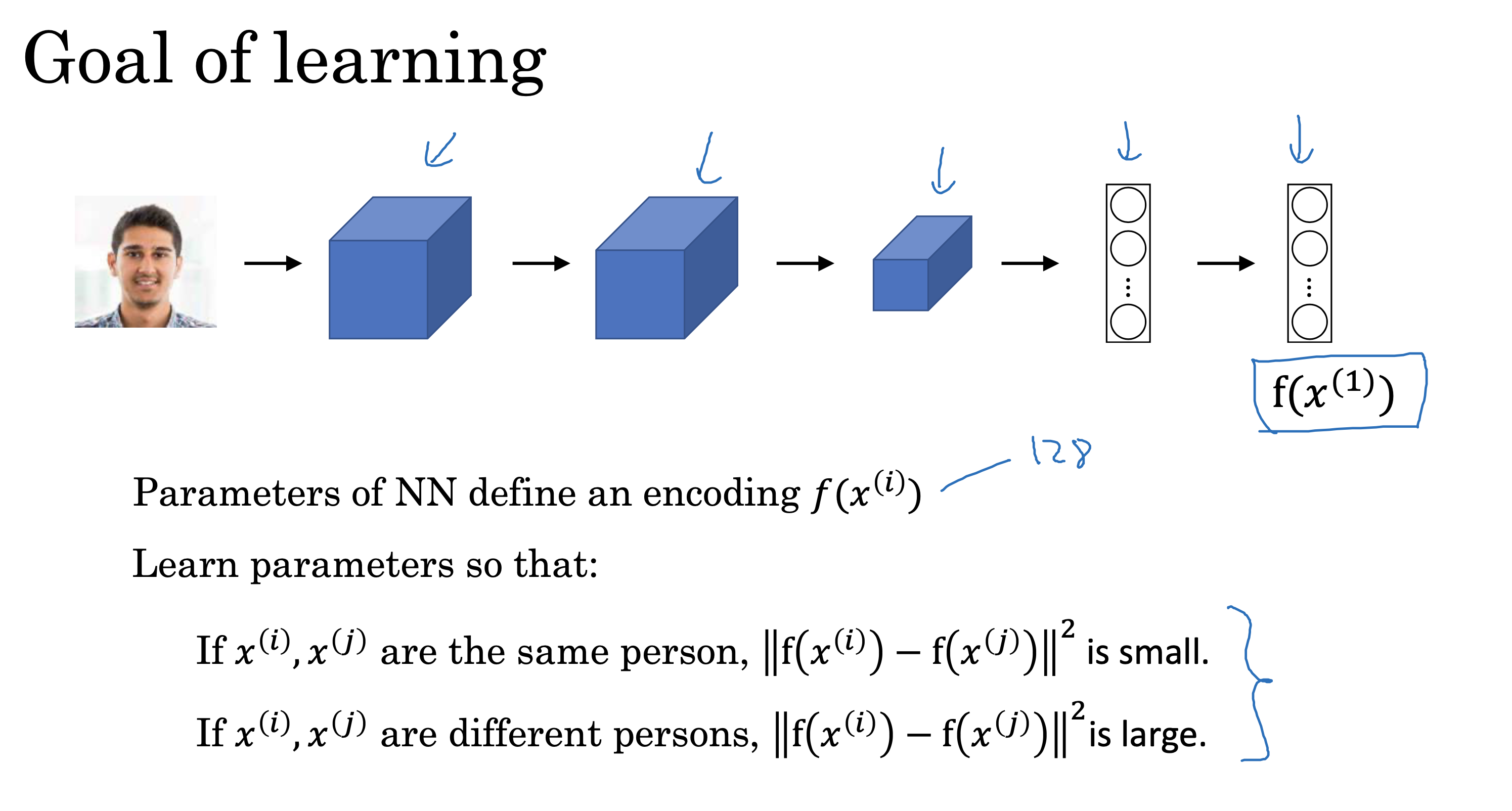
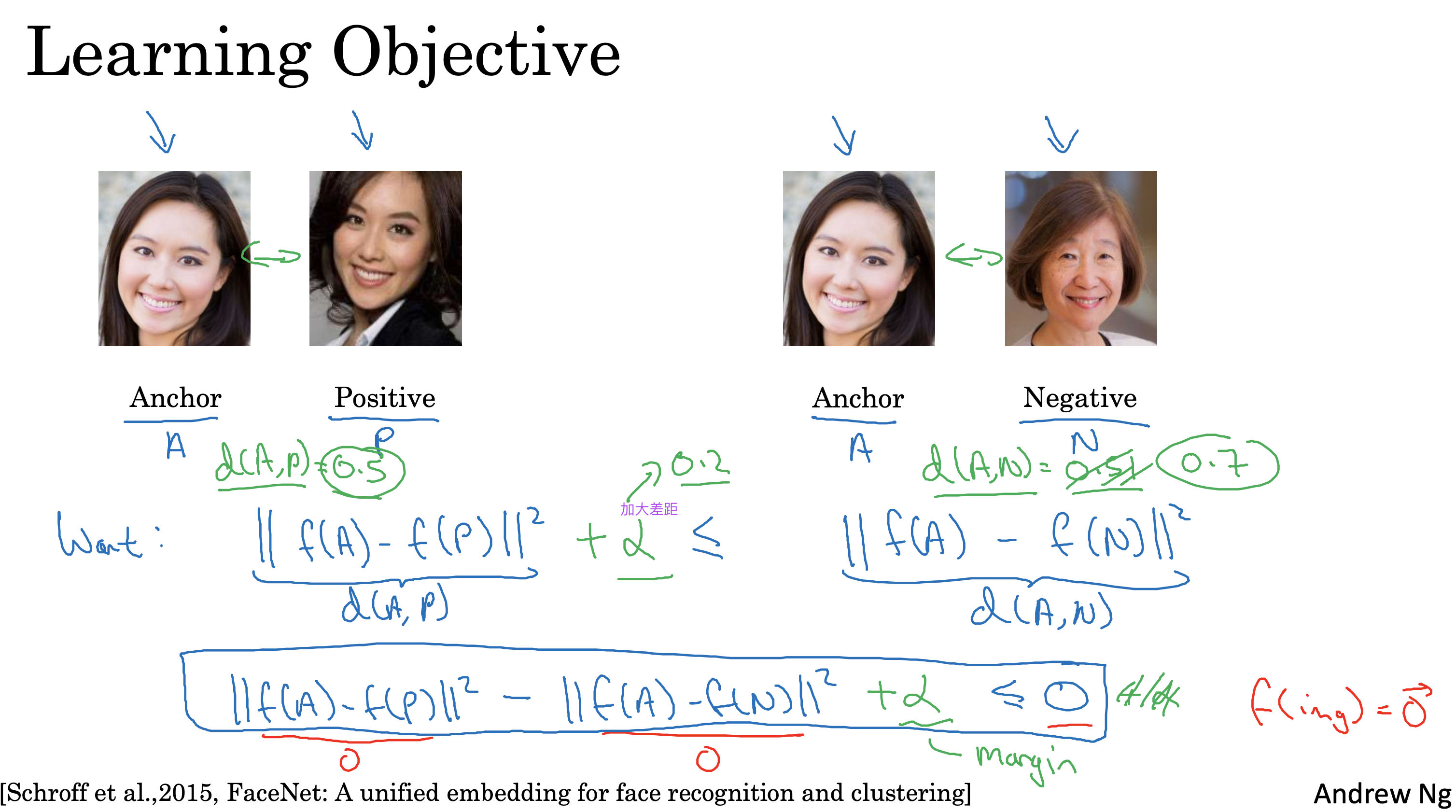
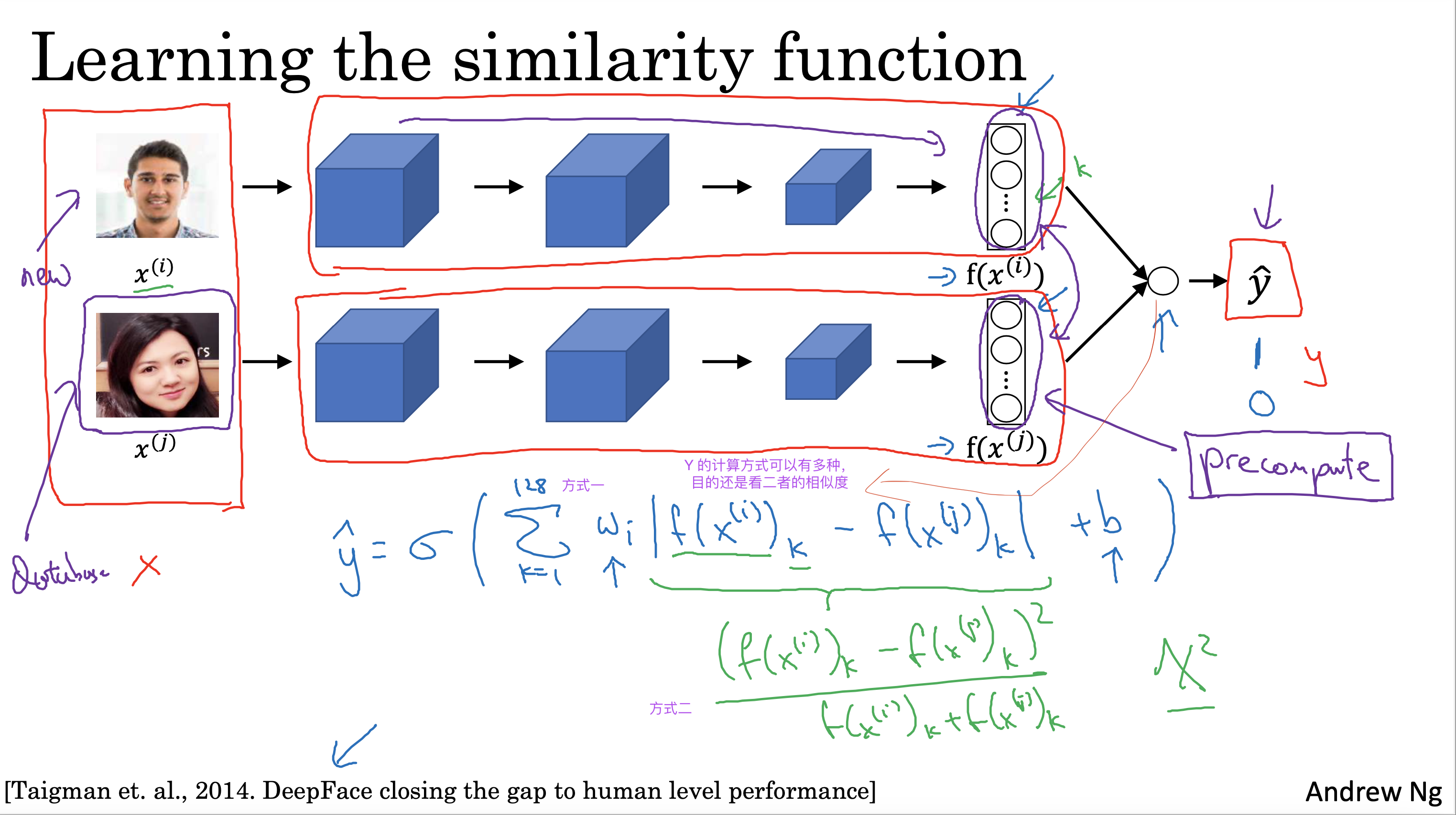
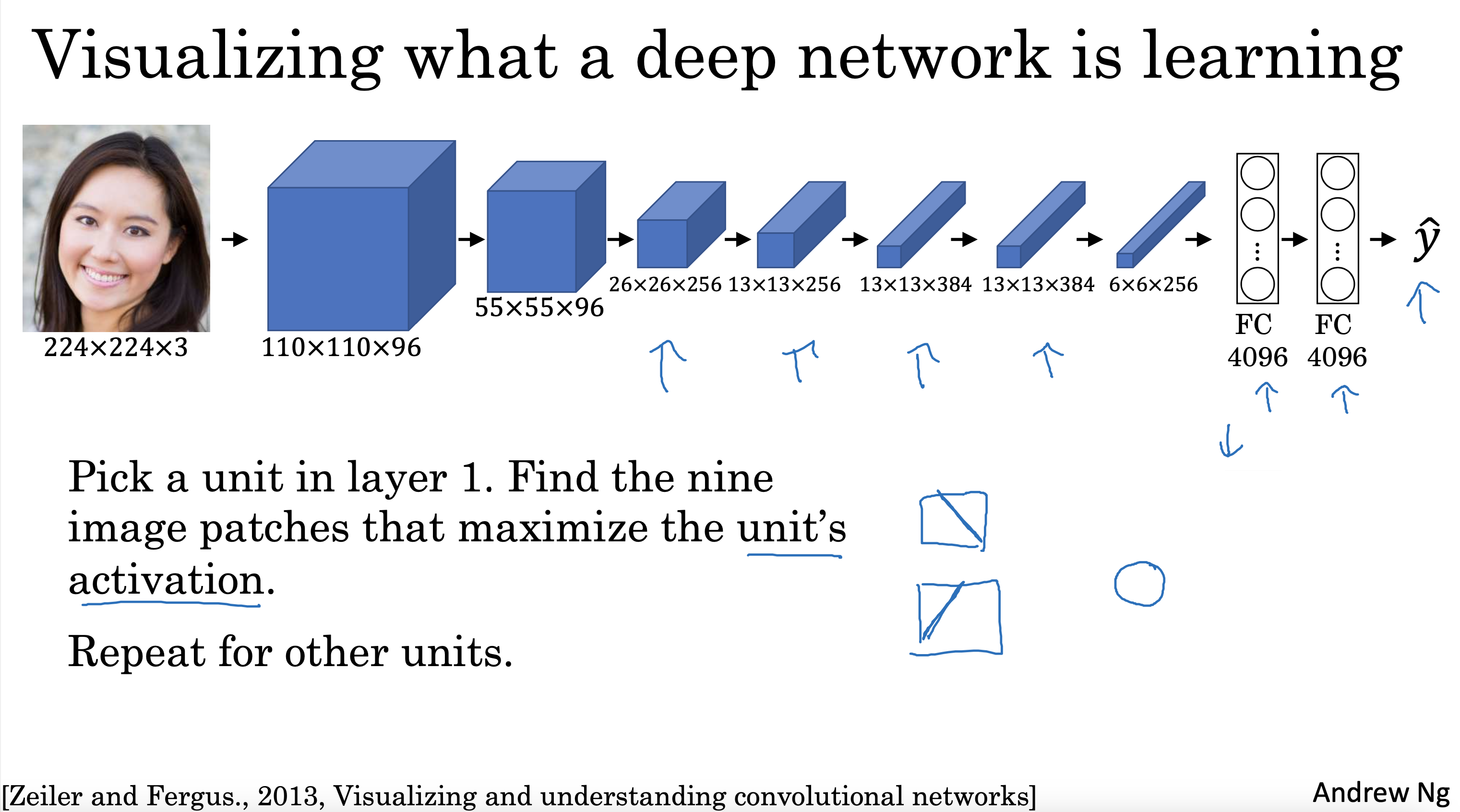
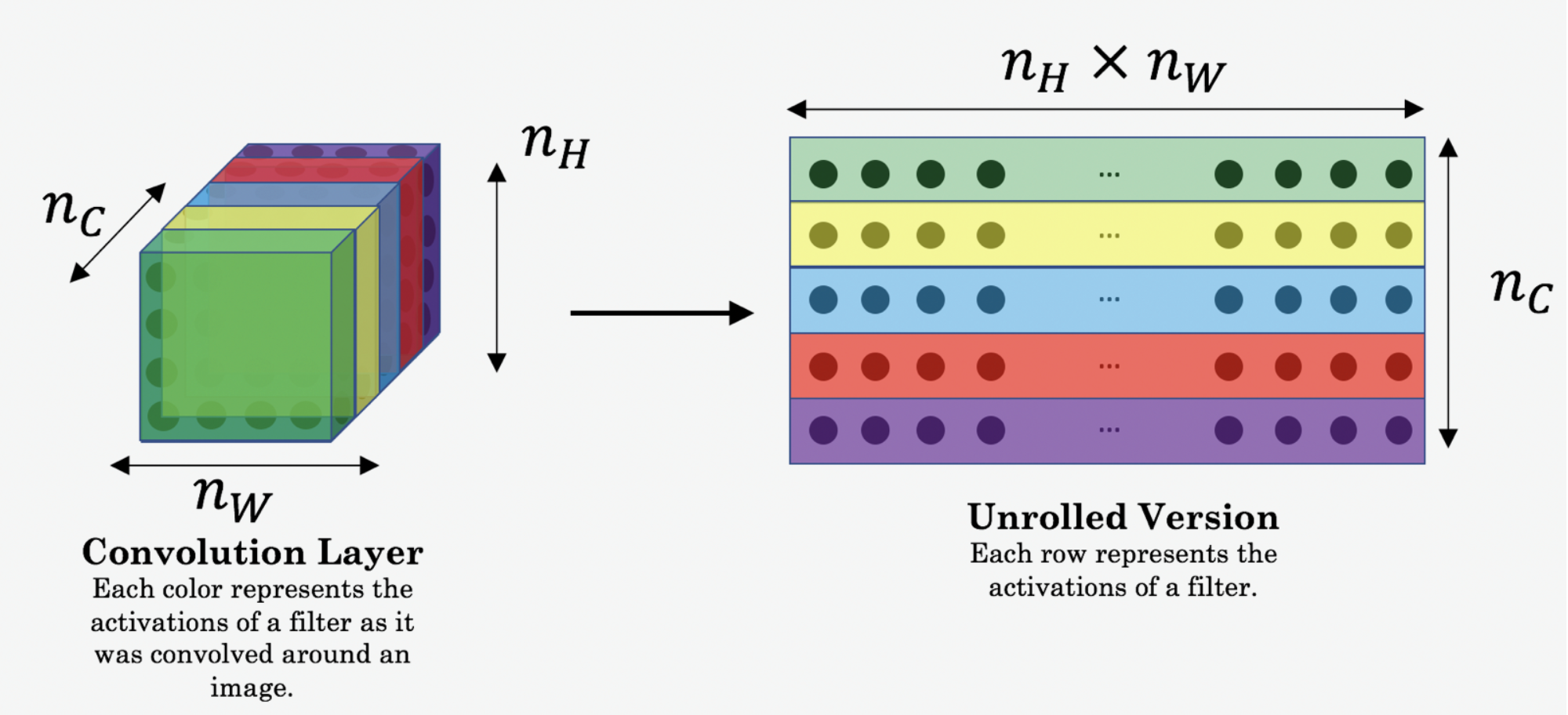
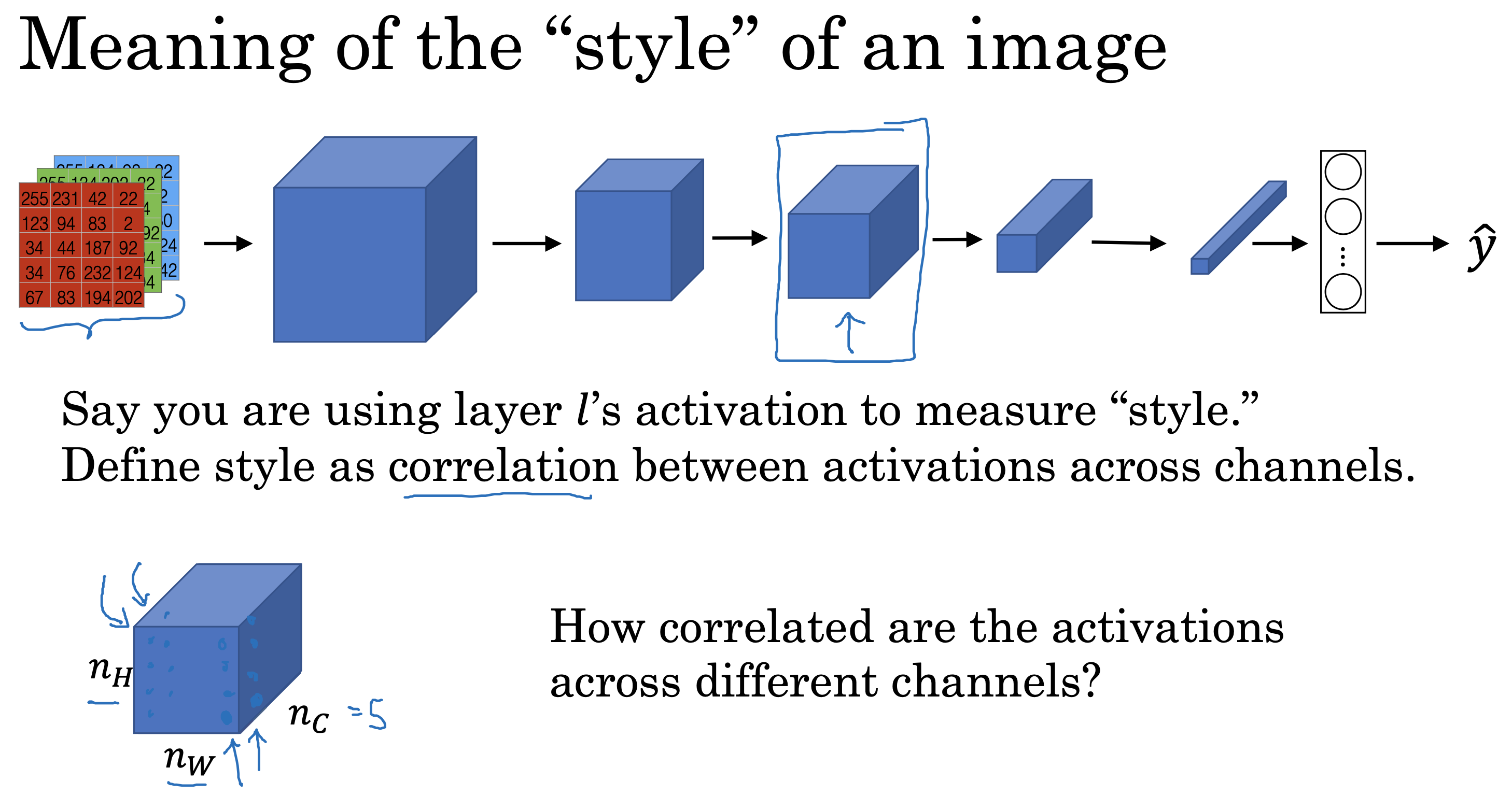
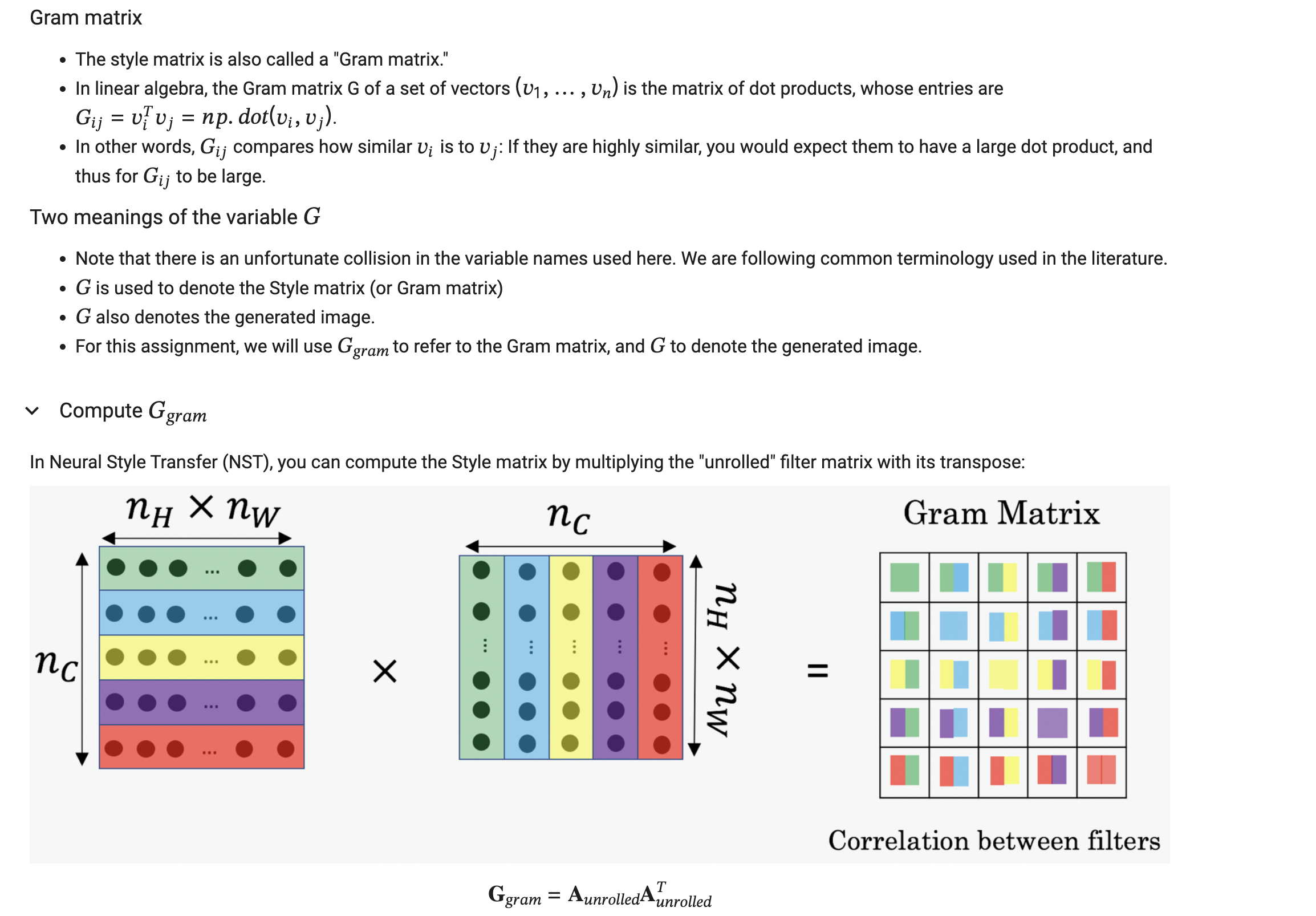
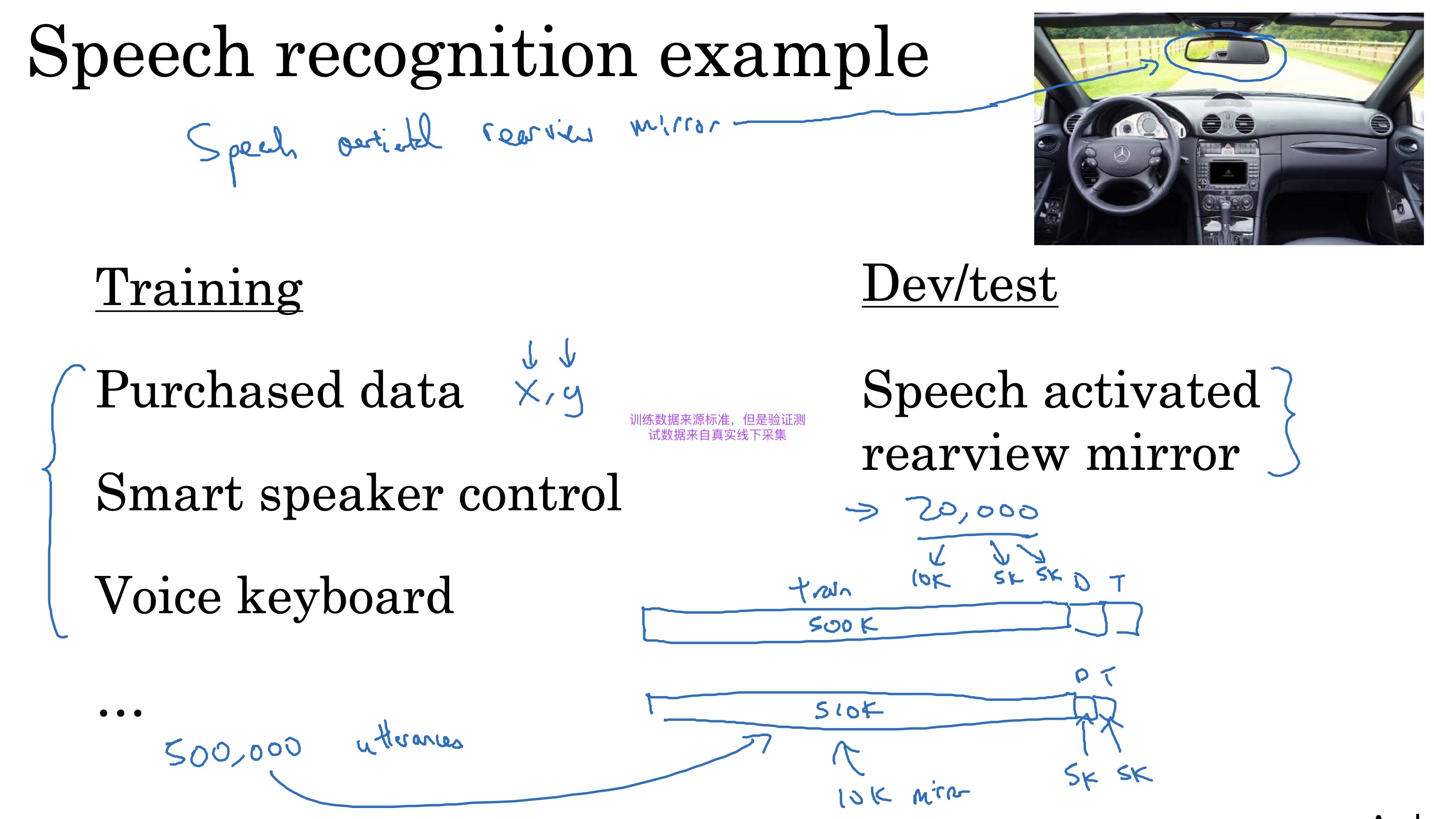
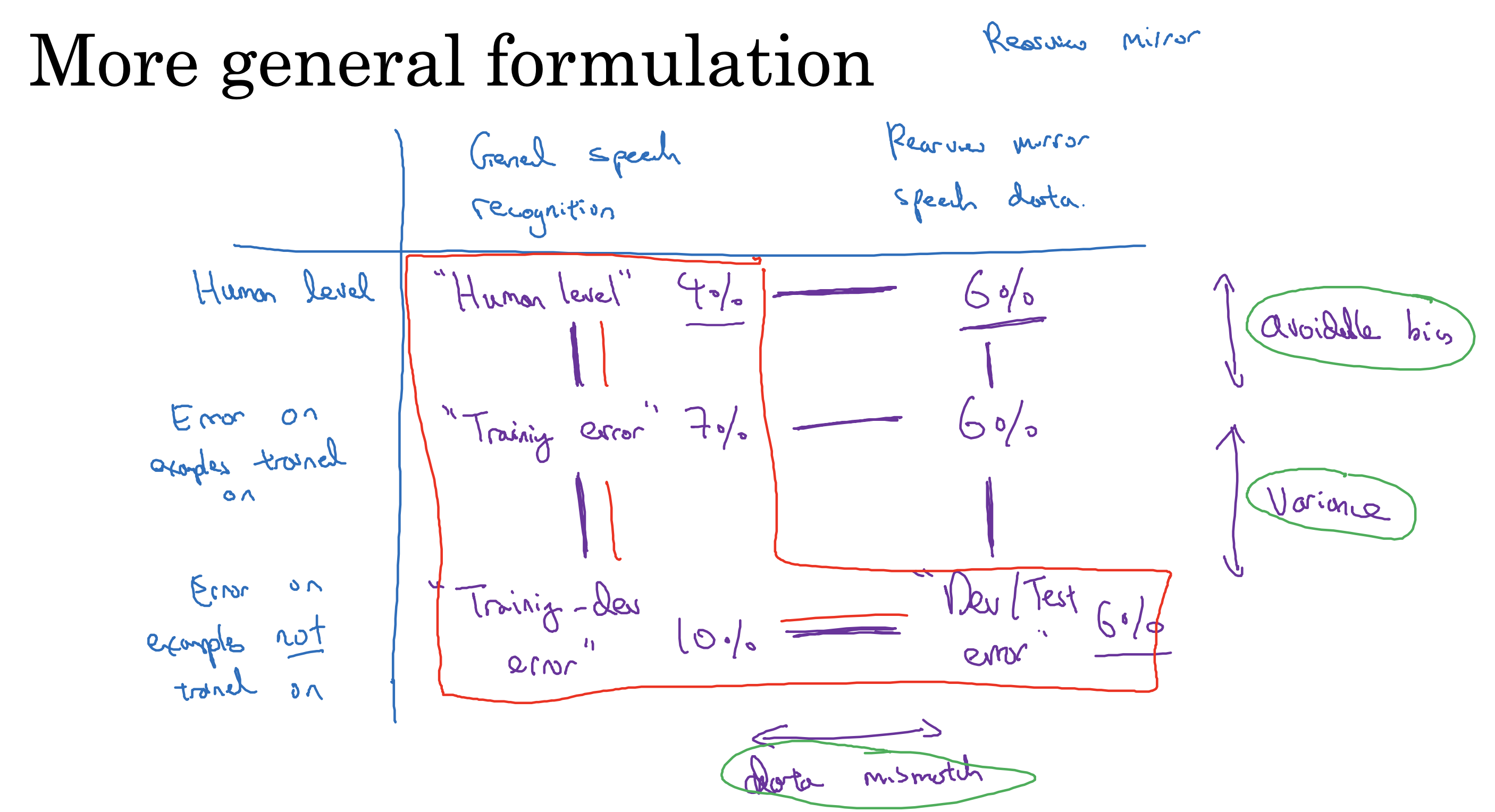
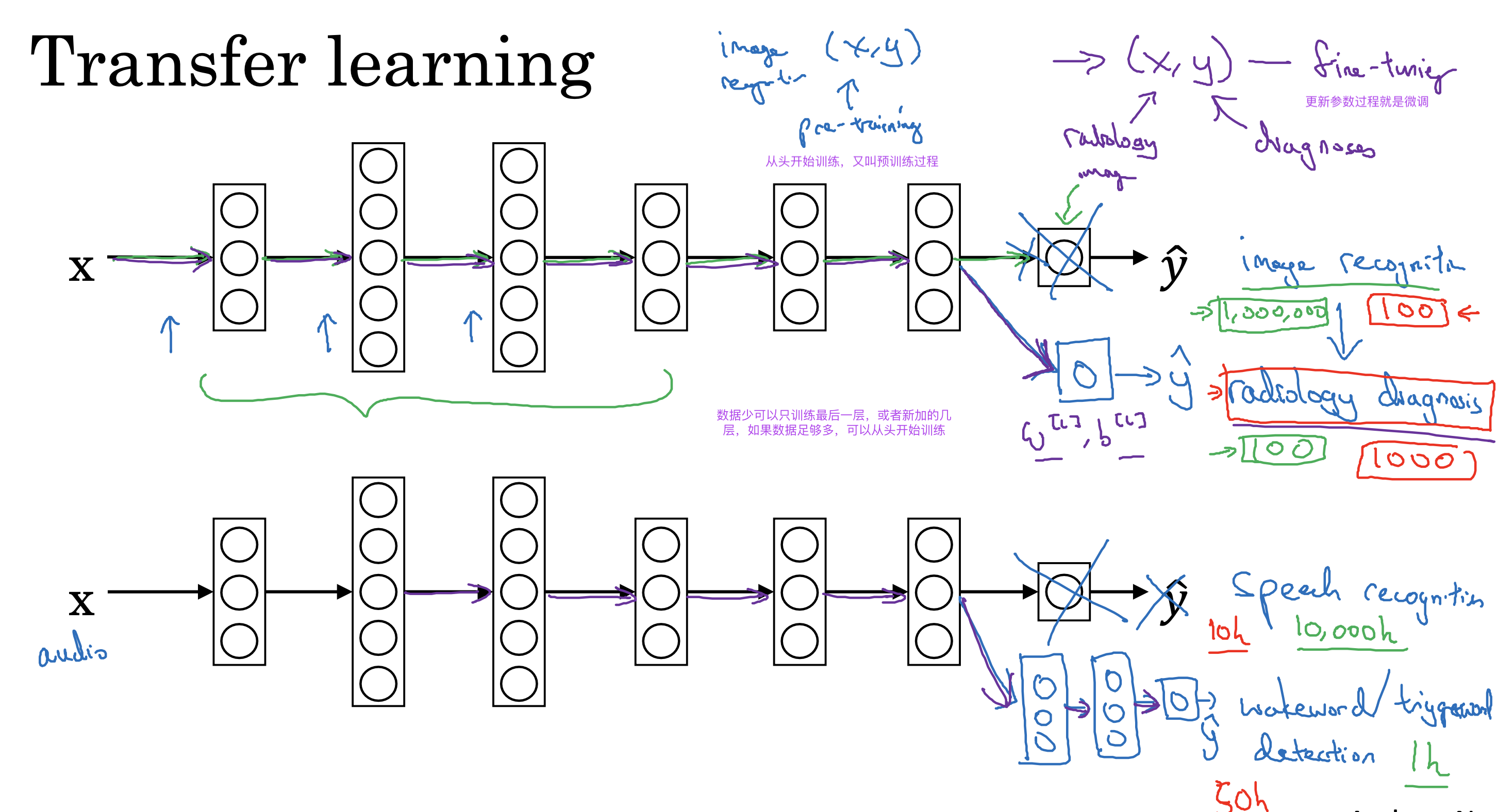
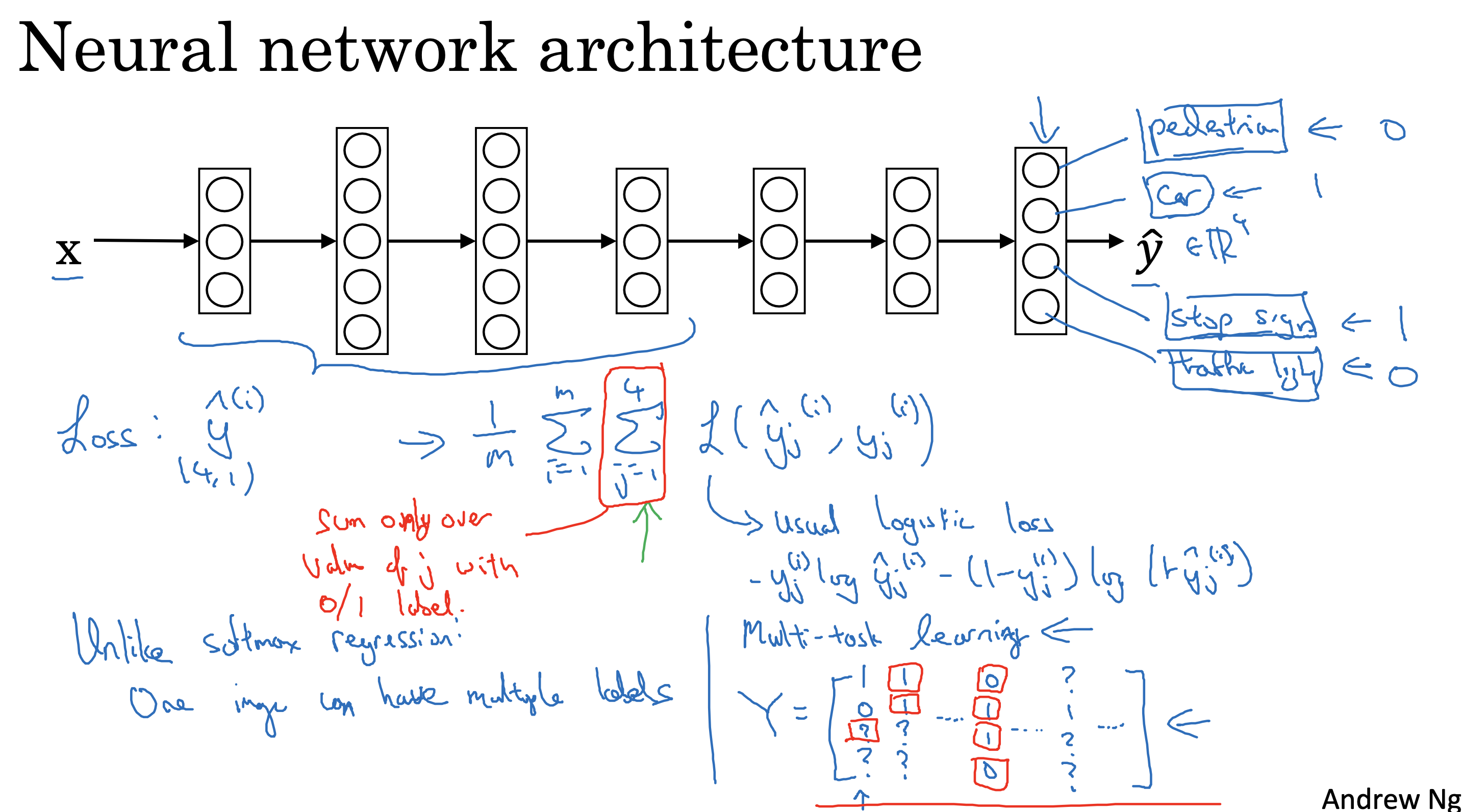
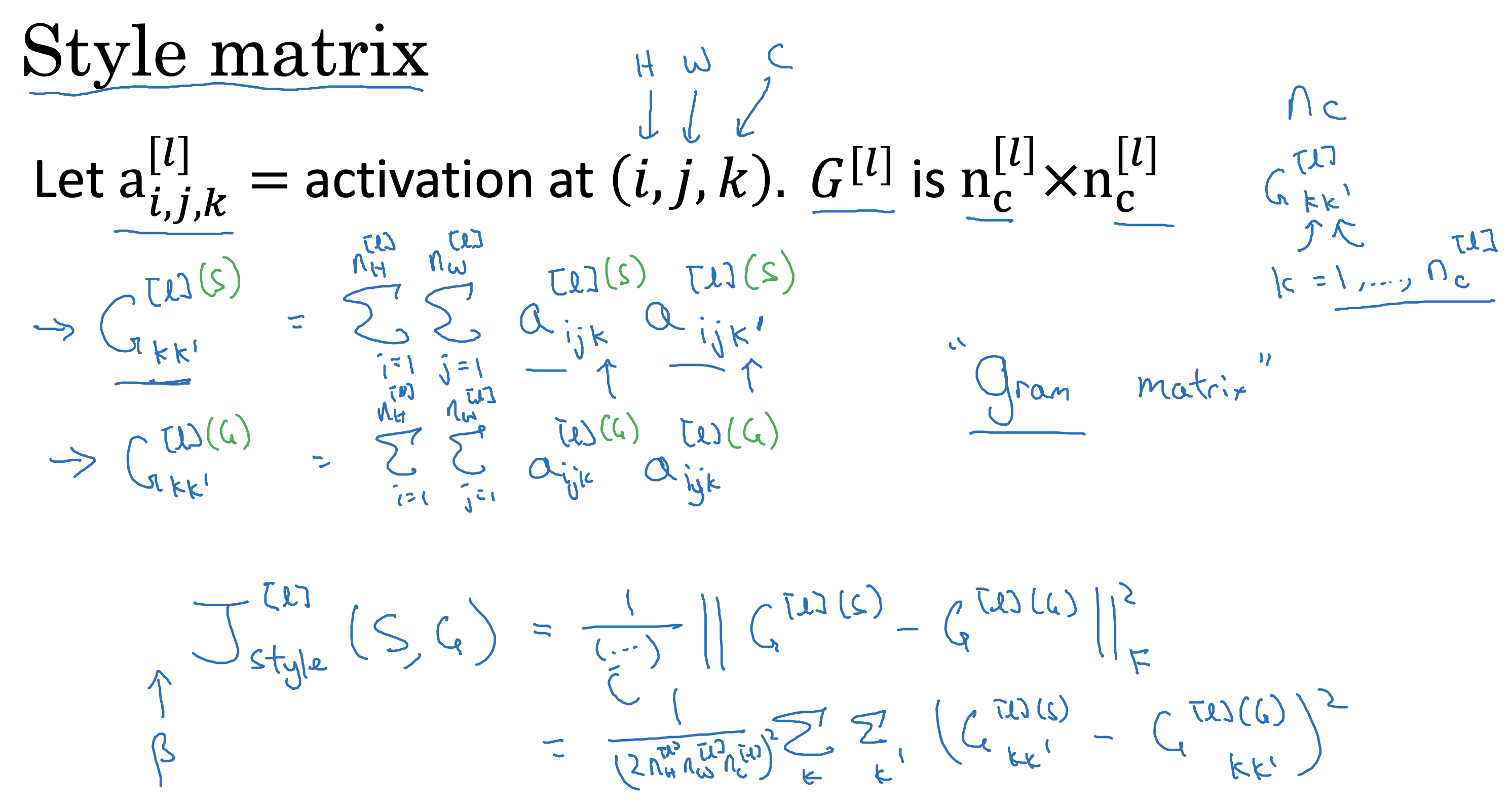文生视频
- 找到相似图片,通过文心一言生成图片提示词
- 将提示词替换下面代码, 在jupyter notebook中运行可以得到5张图片
1 | import json |
- 将图片上传到度加-视频生成,生成依据图片生成的视频
商品评论分析
1 | # Python3.8以上 |
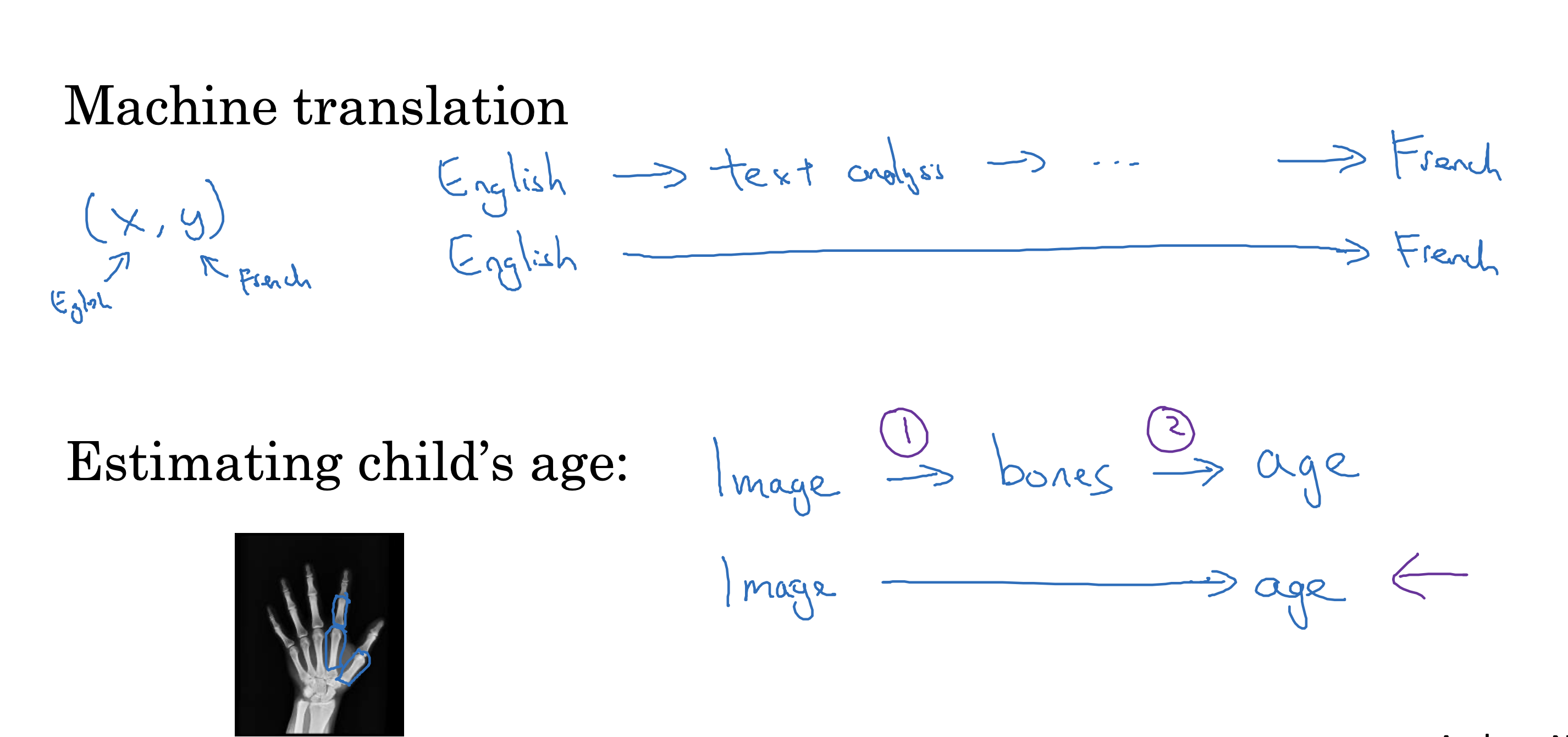
推荐算法1

算法(模型): 建模就是在使用某个算法。
关联算法: 可以实现商品的推荐。
电商: 购买了手机就推荐手机壳。
美团(小象超市): 土豆、黄瓜、鸡蛋、面包、椰子水。—>你历史的购物数据进行关联分析来推荐。
关联算法的阈值:
项集: 每个事物就是一个项集。(土豆、黄瓜、鸡蛋、面包、椰子水)
支持度: 满足最小支持度阈值时就认为数据(项集)之间存在关联规则。可以是多项集之间存在关联规则。0.2 3/5=0.6 牛奶和面包出现的次数/总记录数
001:(牛奶、面包、啤酒、鸡蛋)
002:(方便面、面包、火腿肠)
003:(牛奶、面包、火腿肠)
004:(牛奶、面包、啤酒)
005:(矿泉水、面包、啤酒)
手机和手机壳之间有关联系,还是手机壳和手机之间有关联系呢
置信度: 确定事物之间的关联关系的。0.8
面包和牛奶之间的置信度: 面包和牛奶同时出现的次数/面包出现的次数, 3/5=0.6
牛奶和面包之间的置信度: 牛奶和面包同时出现的次数/牛奶出现的次数 3/3=1
apriori算法
如果事物不满足频繁一项集那么也就一定不满足频繁二项集,以此类推
牛奶、面包、啤酒、鸡蛋、火腿肠、矿泉水、方便面
牛奶: 0.6 面包: 1 啤酒: 0.6 鸡蛋0.2 火腿肠: 0.4 矿泉水: 0.2 方便面: 0.2
牛奶: 面包: 0.6 牛奶: 啤酒: 0.4 牛奶: 鸡蛋: 0.2 面包: 啤酒: 0.6 面包: 鸡蛋: 0.2 啤酒: 鸡蛋: 0.2
fp-tree: 将事物的关联规则加载成一个树形结构
面包: 5
牛奶: 3 啤酒: 3 火腿肠: 1
火腿肠: 1
1 | import pandas as pd |
推荐算法2
1 | <!-- 想要向某个用户去推荐音乐: |


























 )
)