一些基础知识

深度学习会什么会崛起

随着 数据量的增多，计算能力的提高以及算法的进步，使得深度学习的训练周期变短，可以快速进行迭代更新优化
从而用于工业生成

下面以二分类问题为例，复习一下相关的数学知识和概念

损失函数和成本函数

重新理解一下
损失函数是一个训练数据的预测结果和实际值的差
成本函数是所有训练数据的损失函数的平均值

常见求导公式

1.C’=0(C为常数)；
2.(Xn)’=nX(n-1) (n∈R)；
3.(sinX)’=cosX；
4.(cosX)’=-sinX；
5.(aX)’=aXIna （ln为自然对数）；
6.(logaX)’=1/(Xlna) (a>0，且a≠1)；
7.(tanX)’=1/(cosX)2=(secX)2
8.(cotX)’=-1/(sinX)2=-(cscX)2
9.(secX)’=tanX secX；
10.(cscX)’=-cotX cscX；

计算图

向前传播

计算成本函数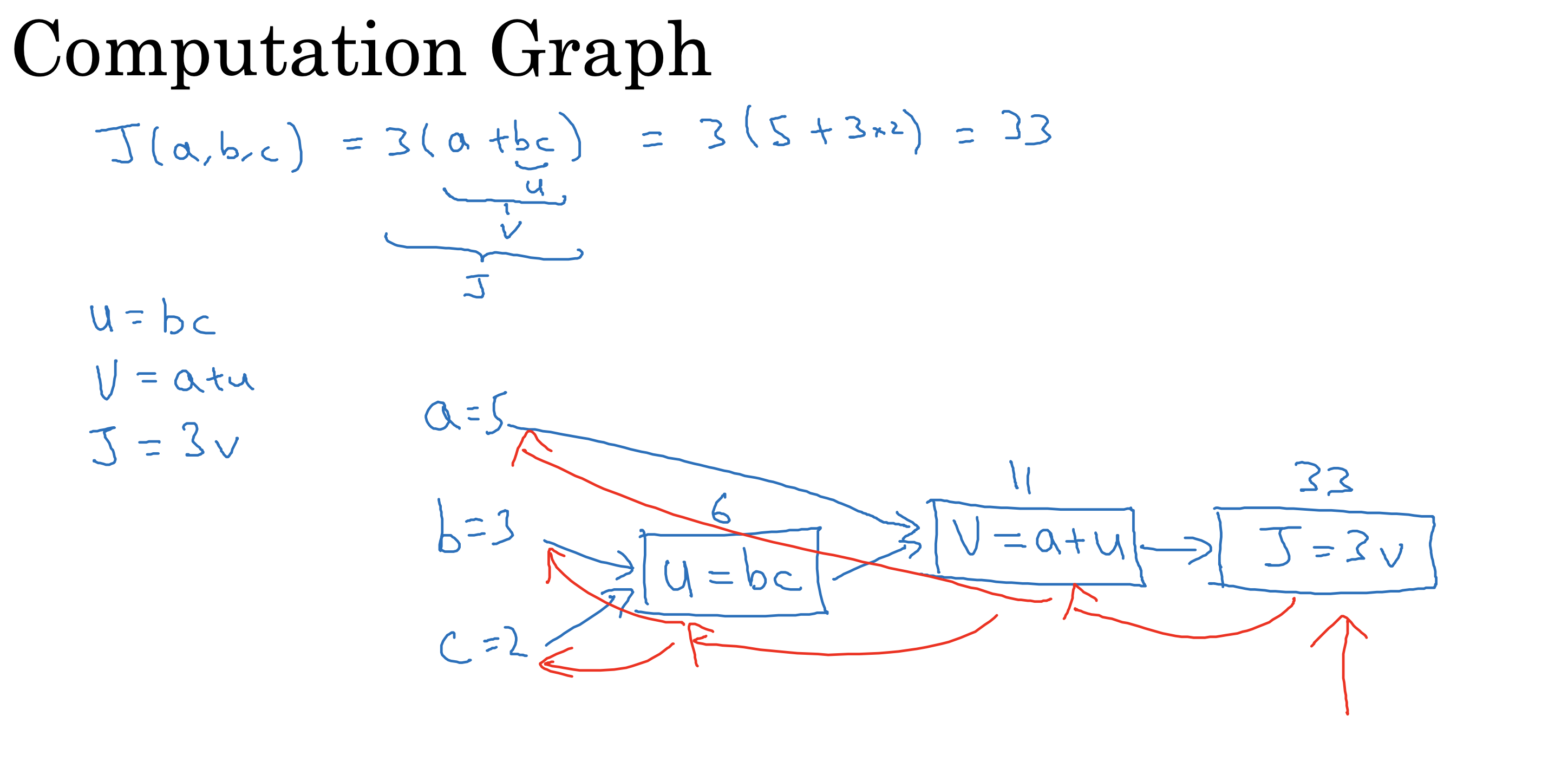

向后传播

通过链式求导得到每一轮计算中参数的导数，从而用于进行梯度下降计算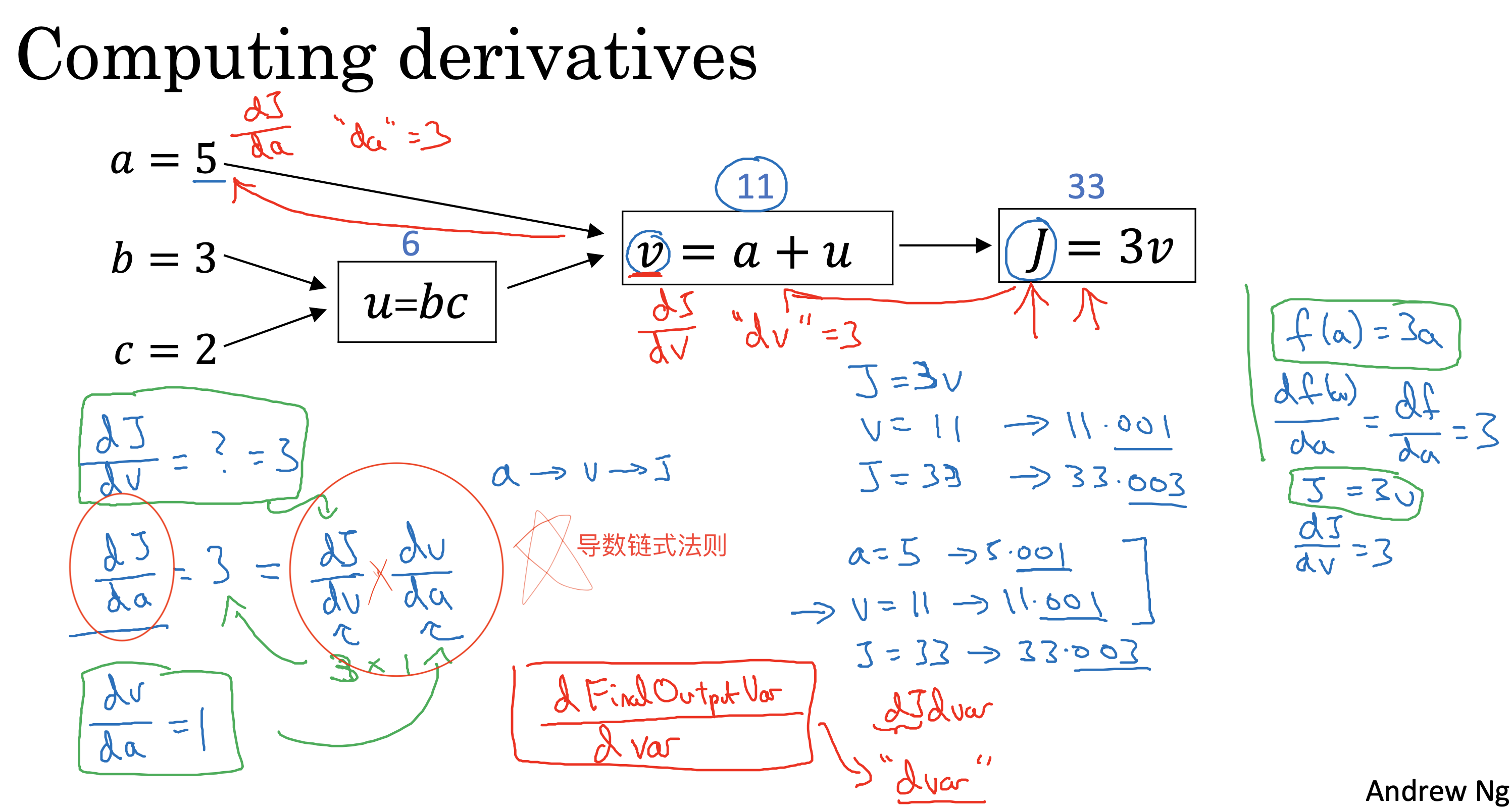

梯度下降计算过程

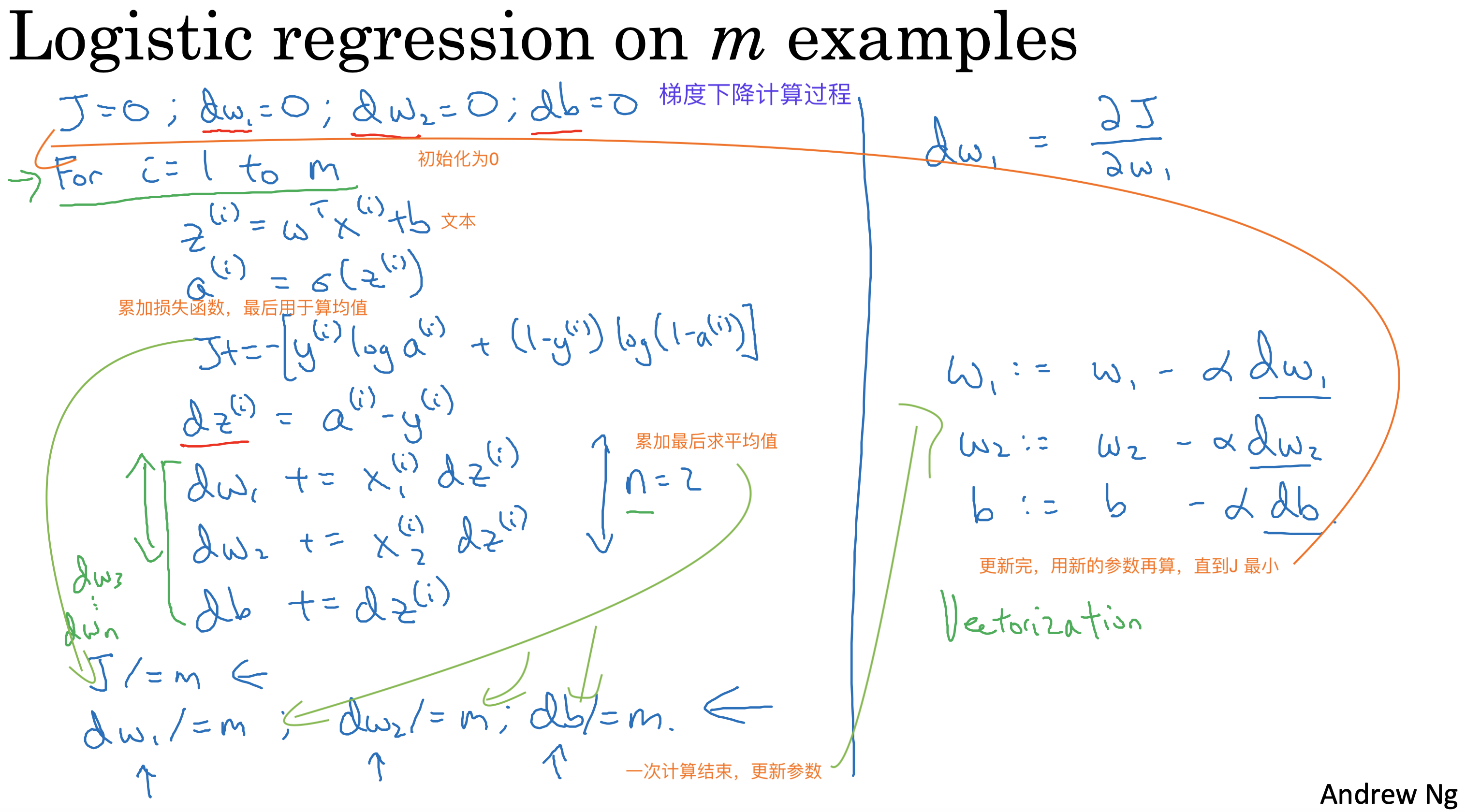
Neural network programming guideline
Whenever possible, avoid explicit for-loops.
避免for-loops循环计算带来的算力损耗，使用向量对上面两次循环(训练数迭代和参数迭代)进行优化，最终只剩训练次数一次loop 循环

广播

通过使用向量的广播计算，可以大幅度减少for循环的计算成本
广播常见的计算过程如下

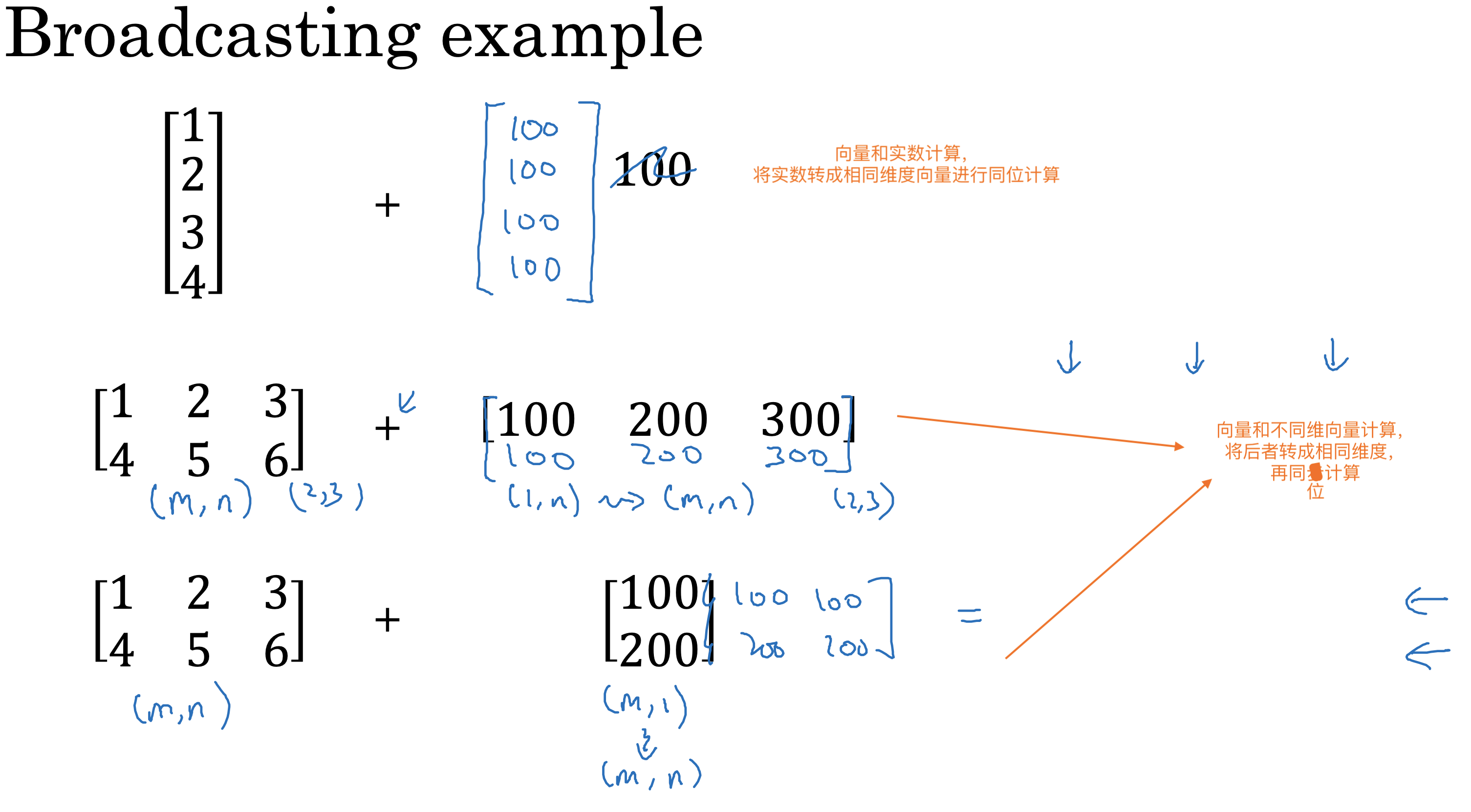
练习

使用广播的运算概念，实现下面的softmax 函数

def softmax(x):
    """Calculates the softmax for each row of the input x.

    Your code should work for a row vector and also for matrices of shape (m,n).

    Argument:
    x -- A numpy matrix of shape (m,n)

    Returns:
    s -- A numpy matrix equal to the softmax of x, of shape (m,n)
    """
    # Apply exp() element-wise to x. Use np.exp(...).
    x_exp = np.exp(x)

    # Create a vector x_sum that sums each row of x_exp. Use np.sum(..., axis = 1, keepdims = True).
    x_sum = np.sum(x_exp, axis=1, keepdims=True)
    
    # Compute softmax(x) by dividing x_exp by x_sum. It should automatically use numpy broadcasting.
    s = x_exp / x_sum
    
    return s

x = np.array([
    [9, 2, 5, 0, 0],
    [7, 5, 0, 0 ,0]])
print("softmax(x) = " + str(softmax(x)))
==>
softmax(x) = [[9.80897665e-01 8.94462891e-04 1.79657674e-02 1.21052389e-04
  1.21052389e-04]
 [8.78679856e-01 1.18916387e-01 8.01252314e-04 8.01252314e-04
  8.01252314e-04]]

github 实验练习

numpy 官网