一些专业术语表达

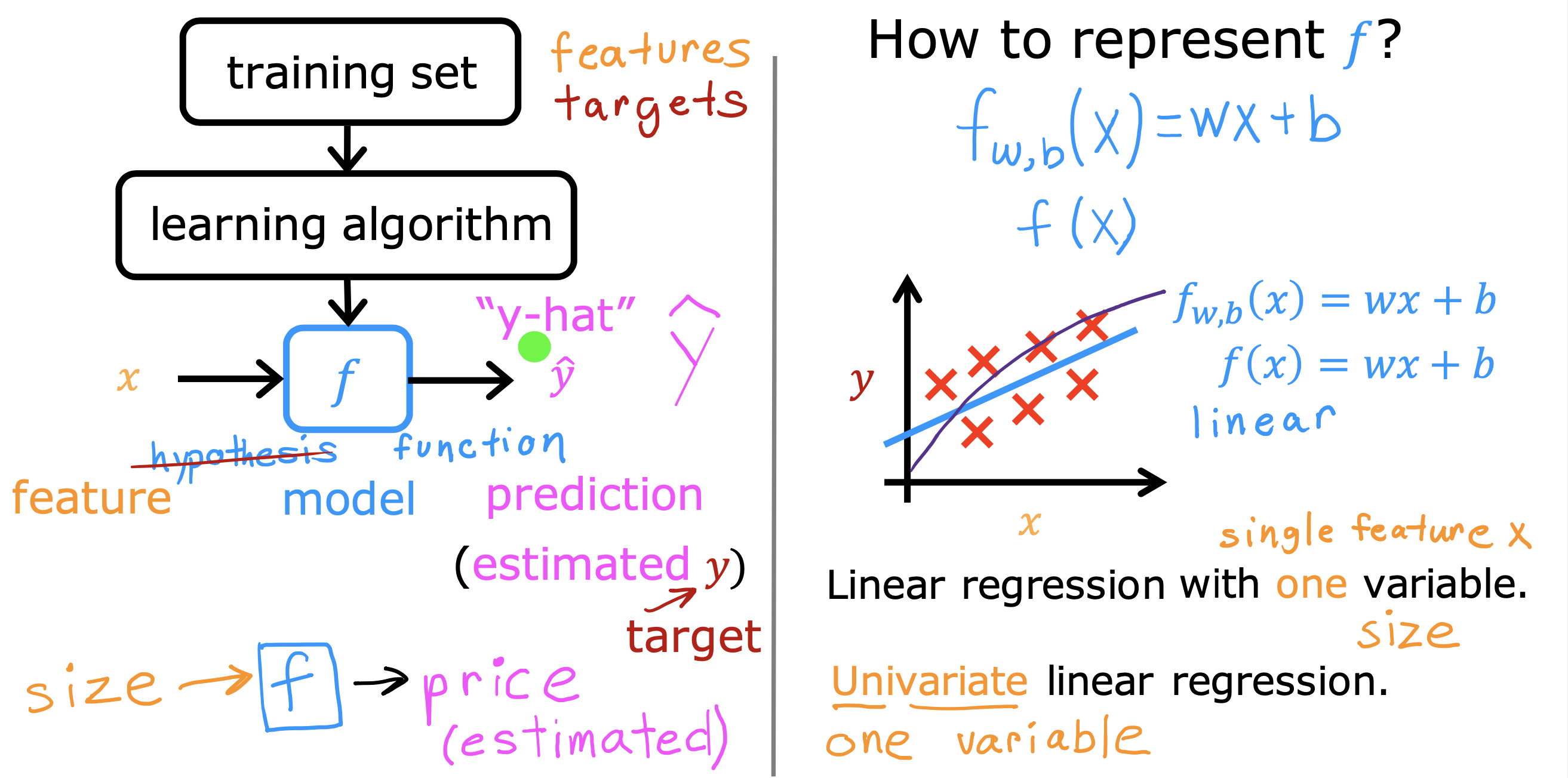
x–> 训练数据入参,特征值,这里仅有一个,这个模型也被叫做 单变量线性回归模型 x(i) 第i个训练数据的x
y–> 训练数据入参,标记值, example 的lable ,y(i) 第i个训练数据的y
y-hat –> 出参,推测值, 模型(f(x)= wx + b) 的 结果值
成本函数
平方误差成本函数

在f(x) = wx+ b 的模型中
w: 斜率
b: 截距,intercepter 直接与Y轴交点距离远点距离
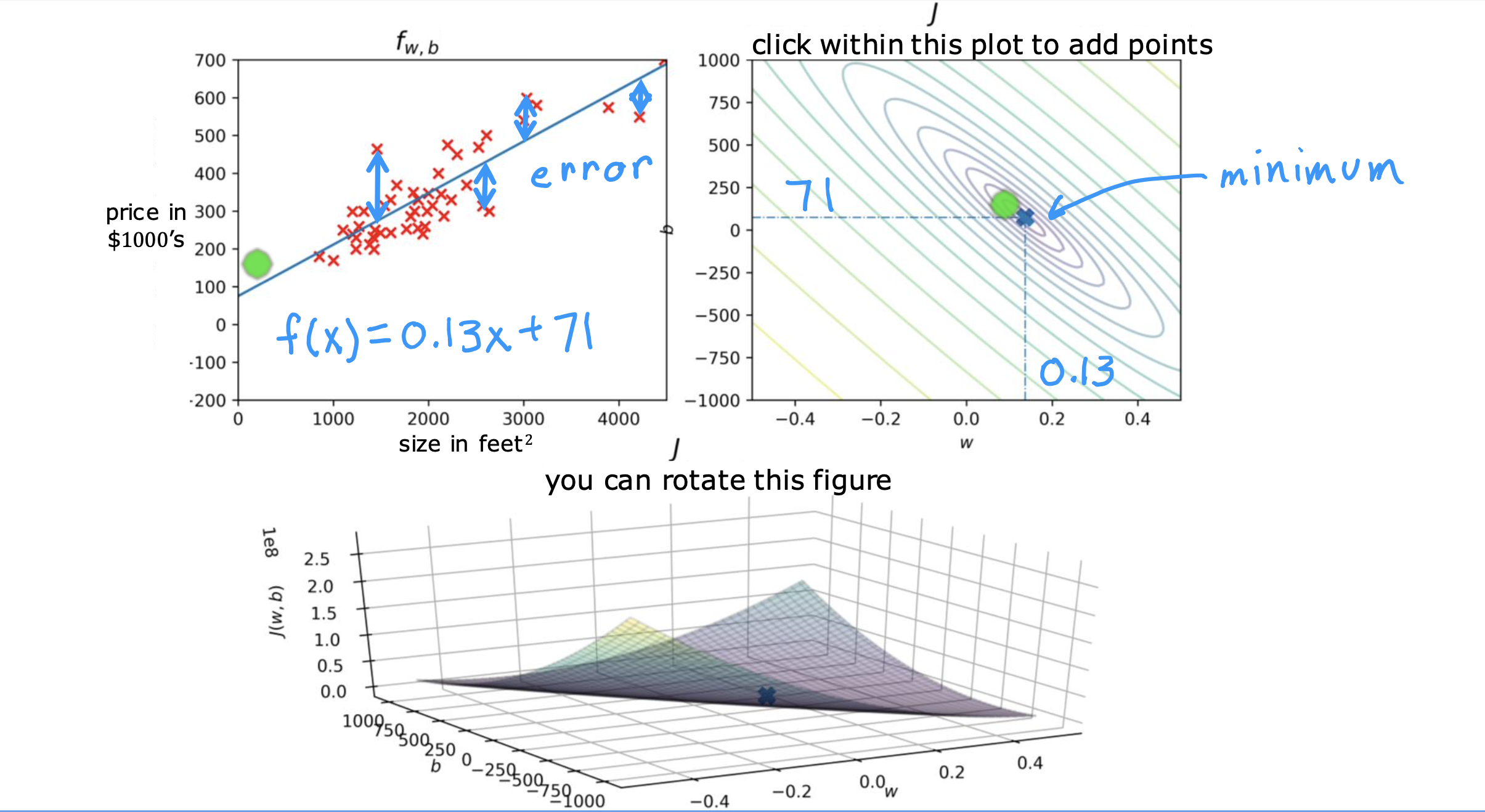
用J(w,b)表示成本函数,找到能够使J(w,b) 的值最小的w和b,就可以找到使f(x)最接近所有测试集的模型,最拟合训练数据的模型
先讨论在b = 0 的情况下,j(w) 随w 变化的趋势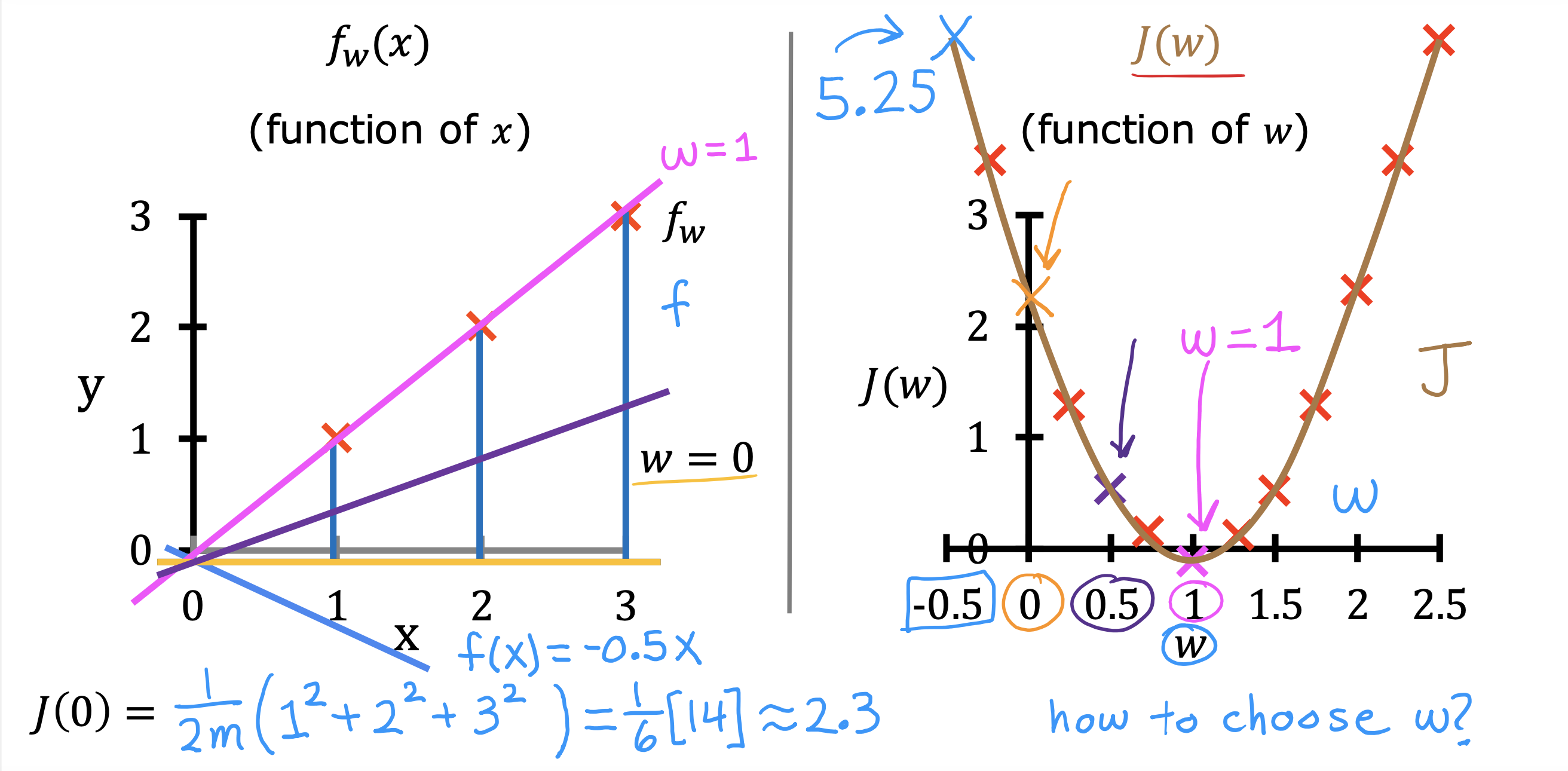
找到使j(w) 最小的w,即U形线最凹的地方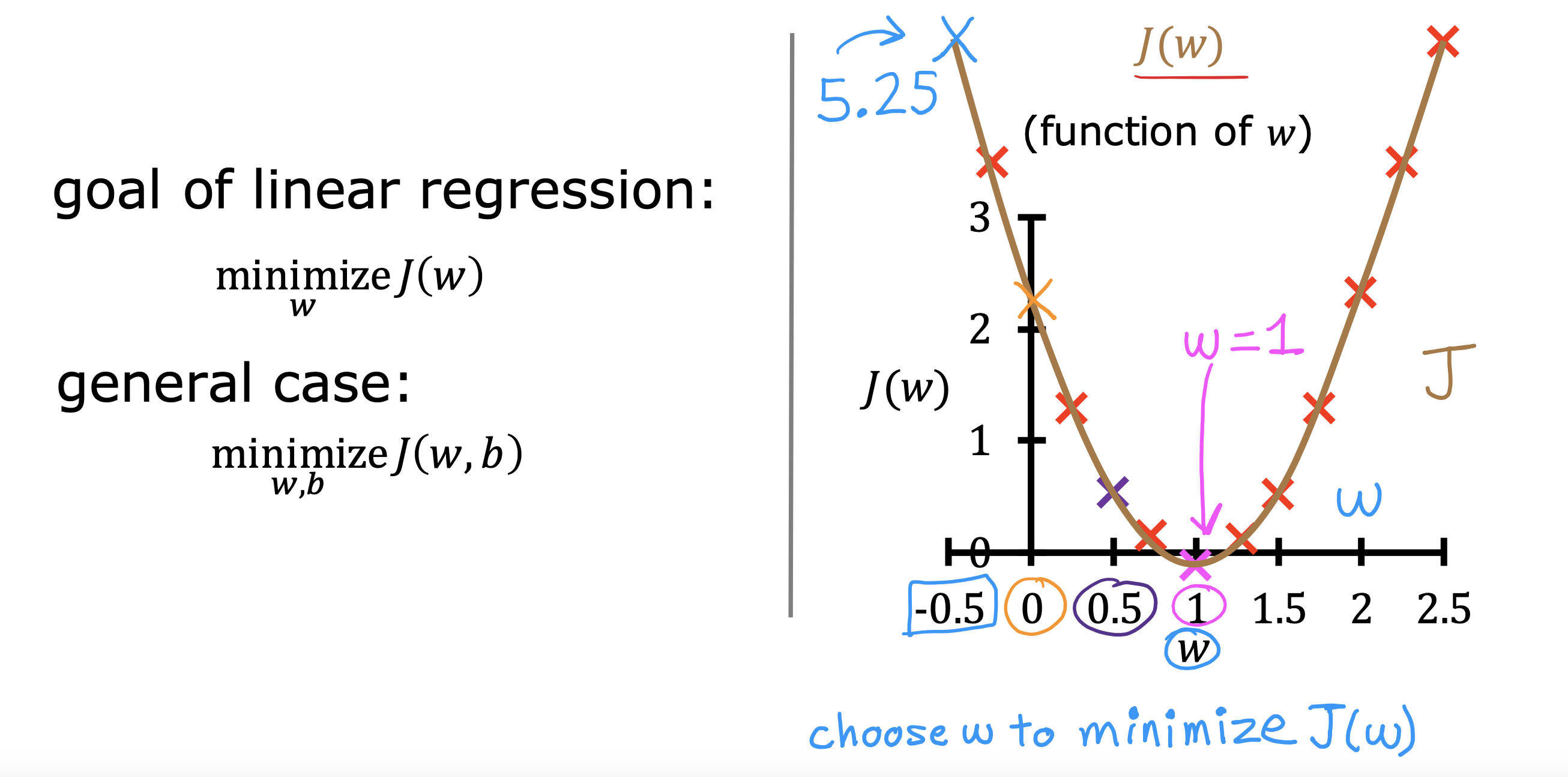
现在把b的变化趋势也加入讨论,j(w,b) 随w,b 变化的趋势,将变成3d 的碗状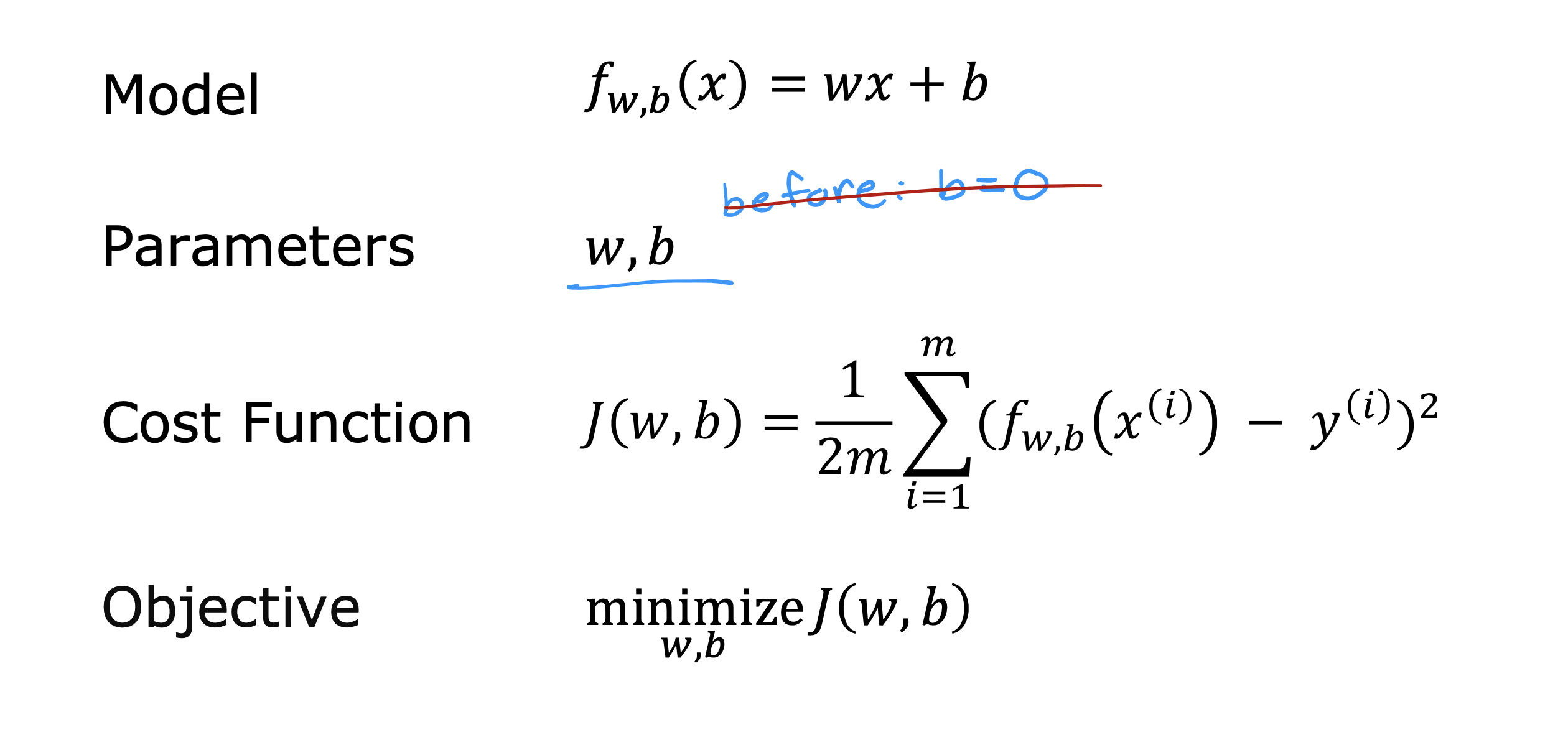
最凹的地方就是J(w,b)值最小的地方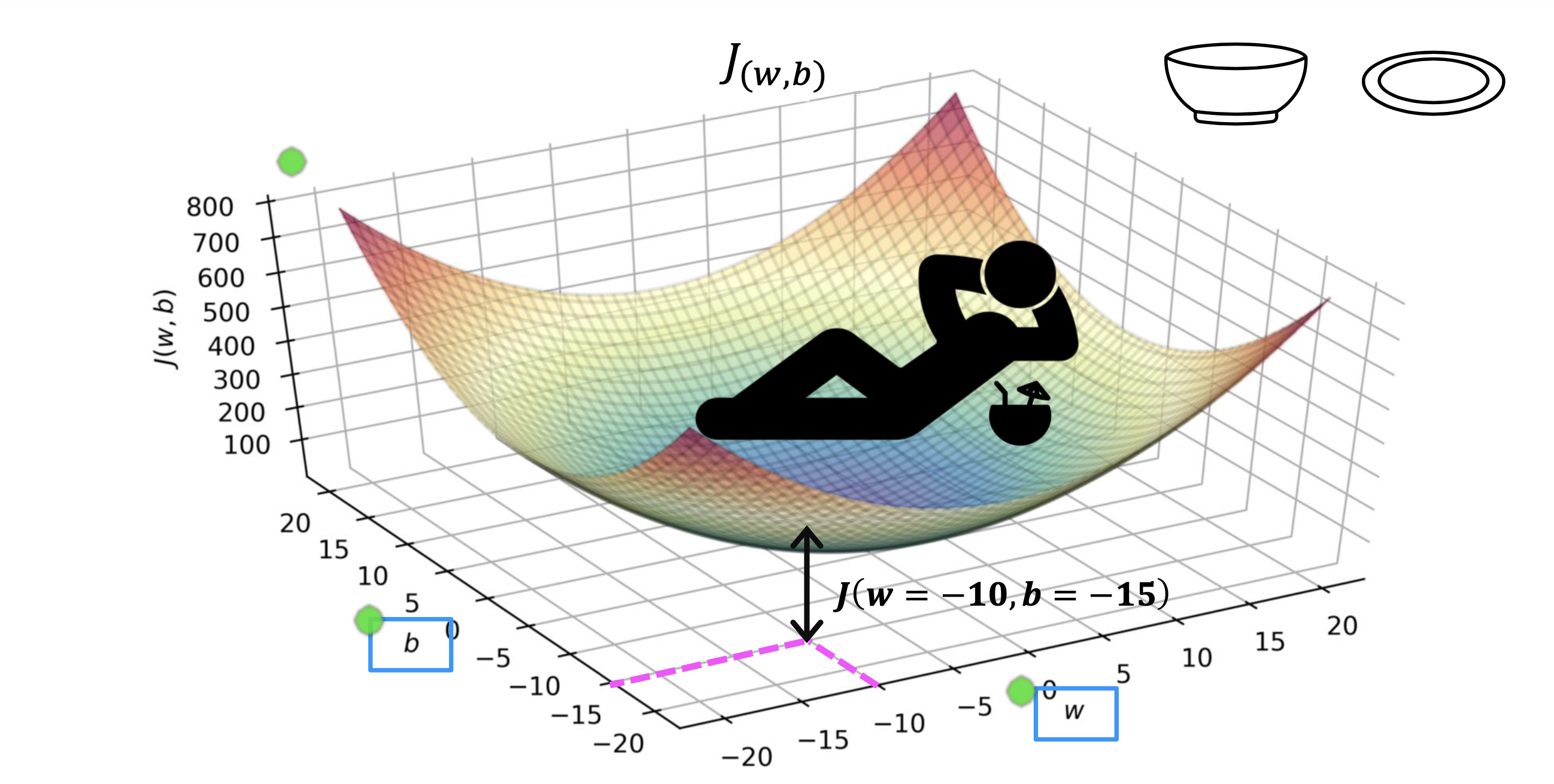
利用等高线的表达方式,换一种视角找J(w,b)的最小值,就是将3D 图进行水平切割,得到关于w,b 的二维椭圆视图
不同(w,b) 组合可能会落在在同一条线上的,相同线上的J(w,b)值一样大
所以能够使J(w,b)值最小的(w,b)值,就是同心圆里面最里面那个圆上的多对(w,b), 当圆极限到一个点时,就只有一对(w,b)使J(w,b)最小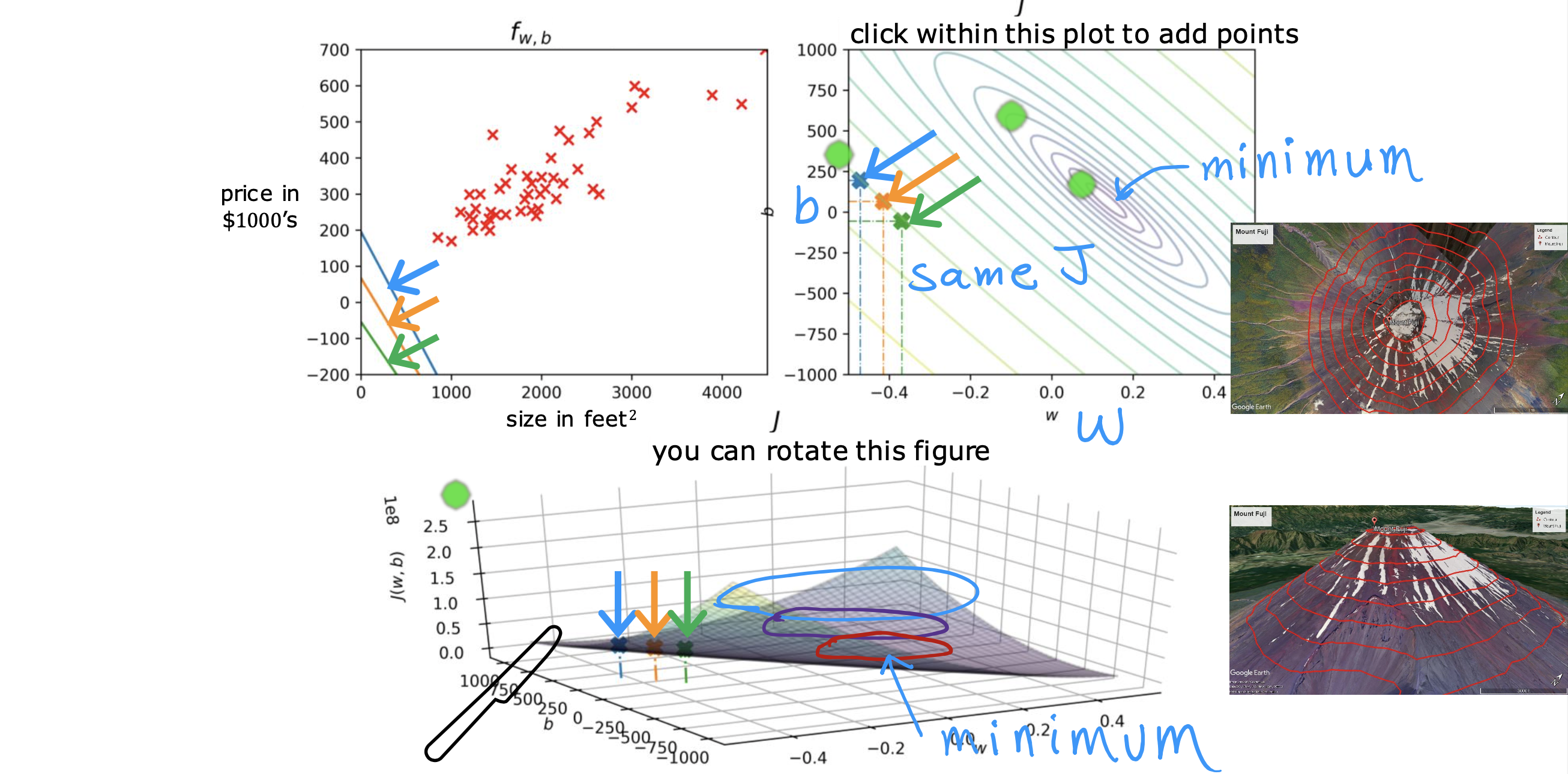
GradientDescentAlgorithm 梯度下降算法
是一种寻找使成本函数达到最小值参数的通用算法,现在不再局限与于f(x) = wx+b 单变量线性模型
对于多变量模型,也就意味着多个w, 这样J(w,b) 就会变成J(w0,…wi,b), J(w0, …wi) 的趋势不再是U形
梯度下降指的是,从一个点出发,环顾四周,找到能够下降的谷底的最快的方向,即梯度最陡的方向,下降一步,每走一步都按最陡方案下降,从而实现最快到达谷底的目的
达到谷底即意味着找到J(w0,…wi,b)最小值
但是梯度下降有一个特性,就是,虽然从同一点出发,如果第一步选择反向不同,或者走的方式不同,肯定会到达不同谷底
不同谷底意味着不同的J(w0,…wi,b)最小值,这些最小值,都叫做局部最小值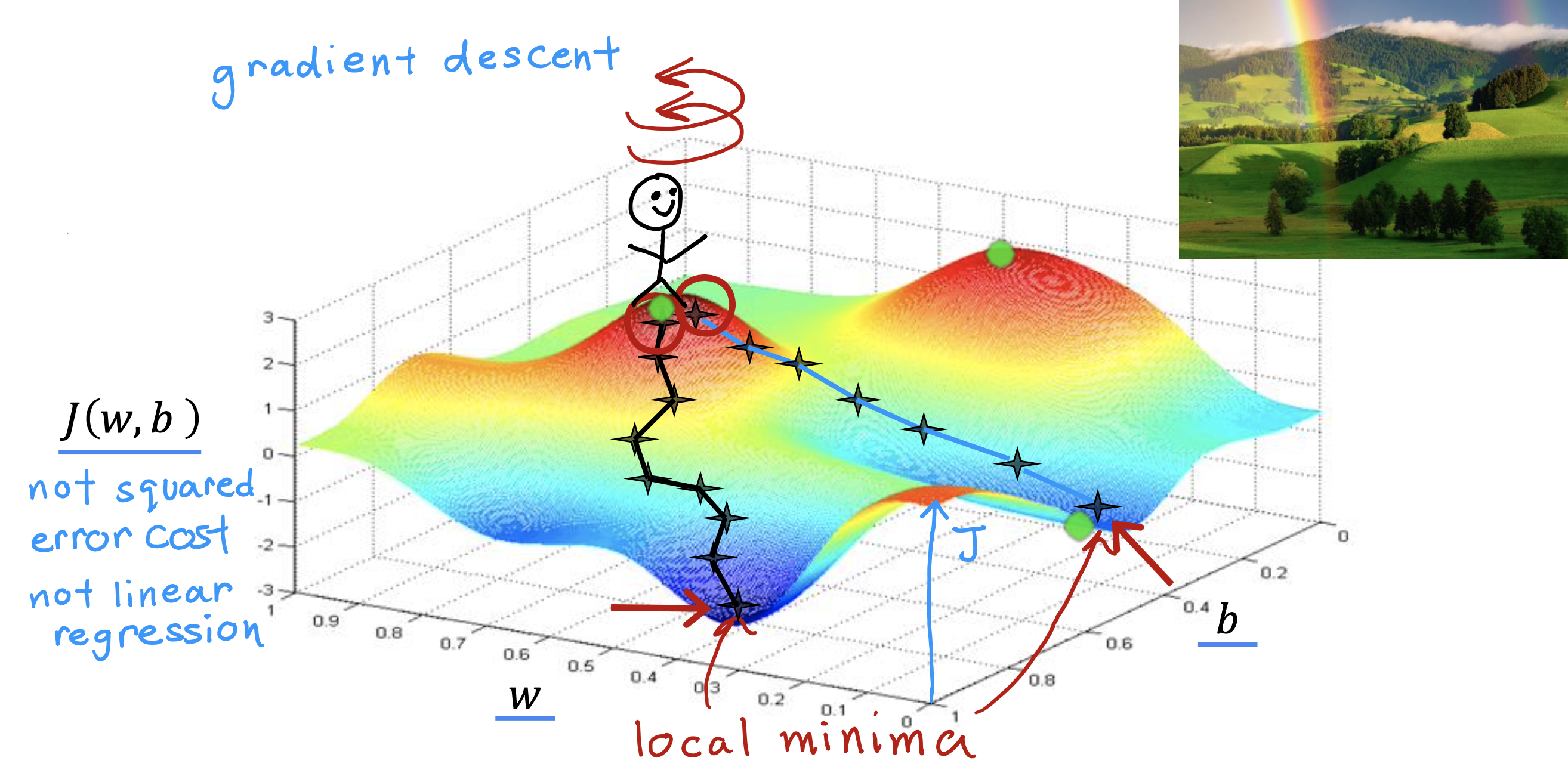
算法实现与理解
J(w,b)关于w 导数 表征 U形趋势线上随w 变化的梯度值,也就是斜率
前面的系数α表征 下坡的步伐大小 是一个0-1 的正小数值,称为学习率
w,b 同时变化,同时更新
当梯度大于0时,temp_w 逐渐变小,J(w,b) 的值也逐渐变小
当梯度小于0 时,temp_w 逐渐变大(负斜率,绝对值在变小), J(w,b)的值逐渐变小
说明J(w,b) 的值随梯度的变化符合随w的变化趋势
当斜率绝对值逐渐变小时,就是都朝J(w,b) 最小值聚拢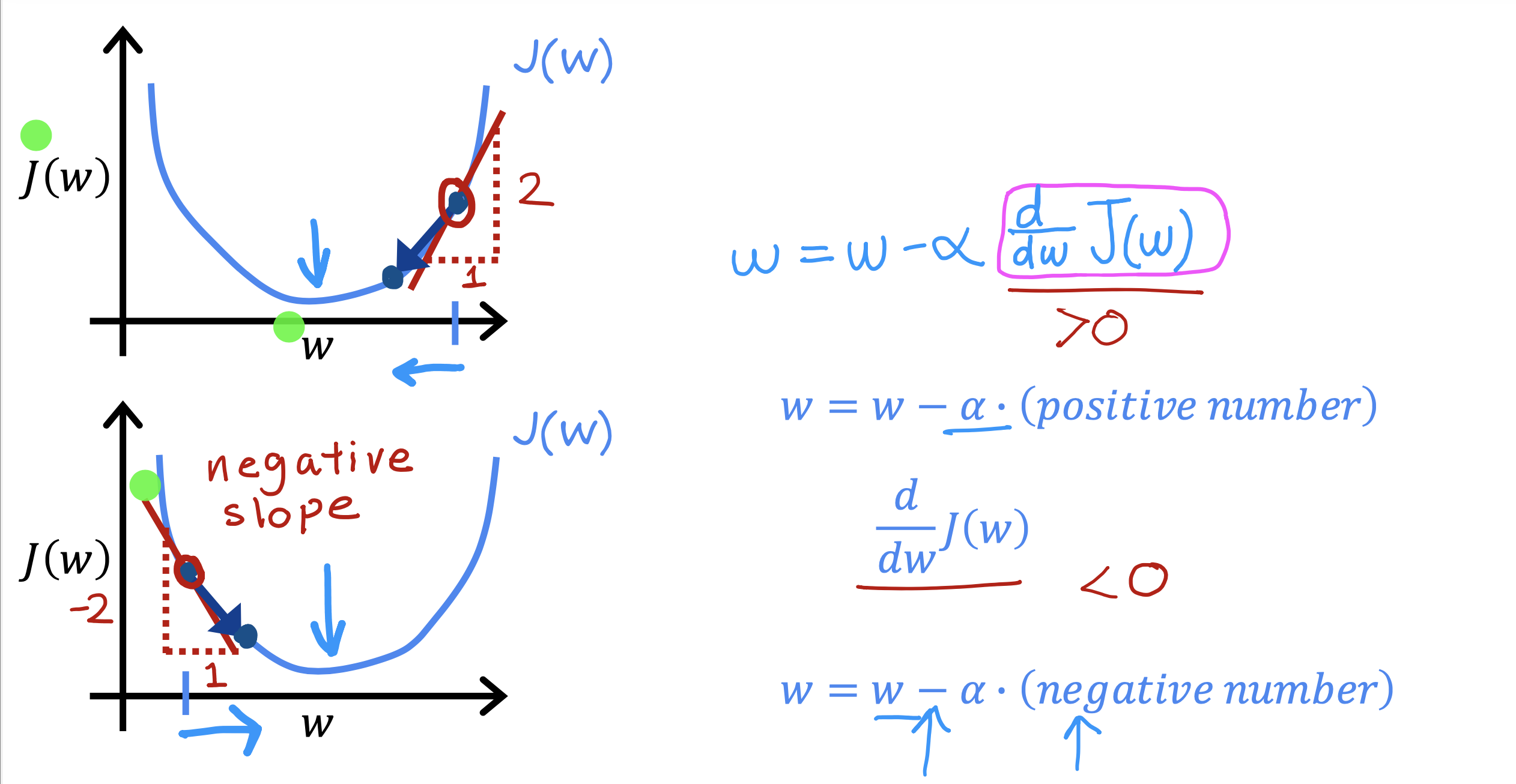
实验
关于学习率
太小会增加计算步骤,从而使梯度算法变慢
太大可能导致过冲,永远无法到达最小值;甚至无法实现聚拢趋势,导致发散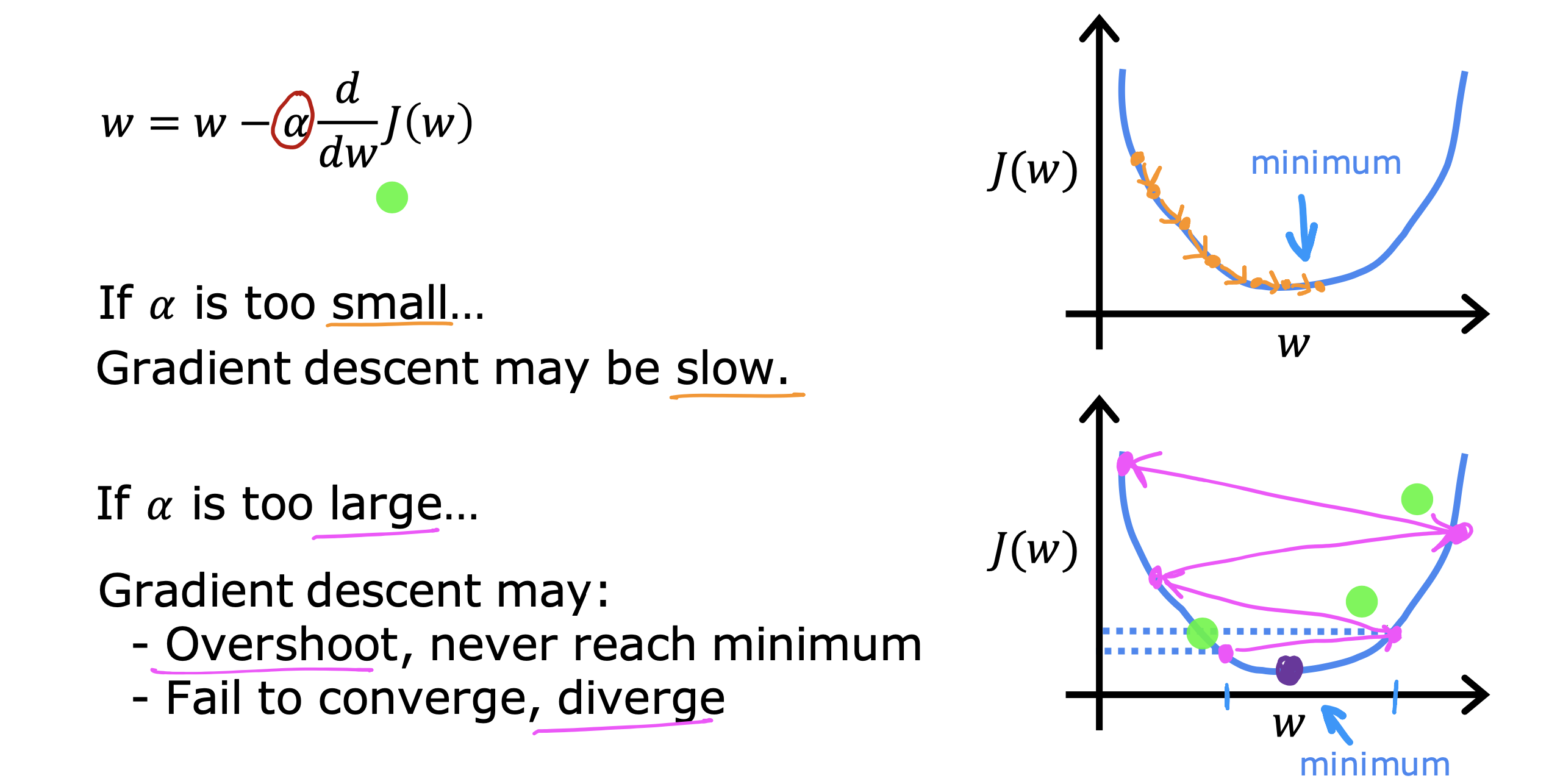
局部最小值
如果当前参数已经使得成本函数到达一个局部最小值,那么J(w,b) 关于w 导数值将会是0,那么temp_w 会始终停留在一个固定的值,不再变化
梯度下降算法将不会再进行下一步的计算,保持当前参数在当前的这个一个局部最小值的状态
随这个梯度下降,我们可以知道我们正在朝成本函数最小值靠近,在学习率固定情况下,更新步骤也在下降(斜率本身朝0在逐渐变小),说明没有学习率的变化,也能到达局部最小值
但如果同时将学习率调小,降低下降的步伐,可以更小幅度的一点点接近最小值,最终找到成本函数最小值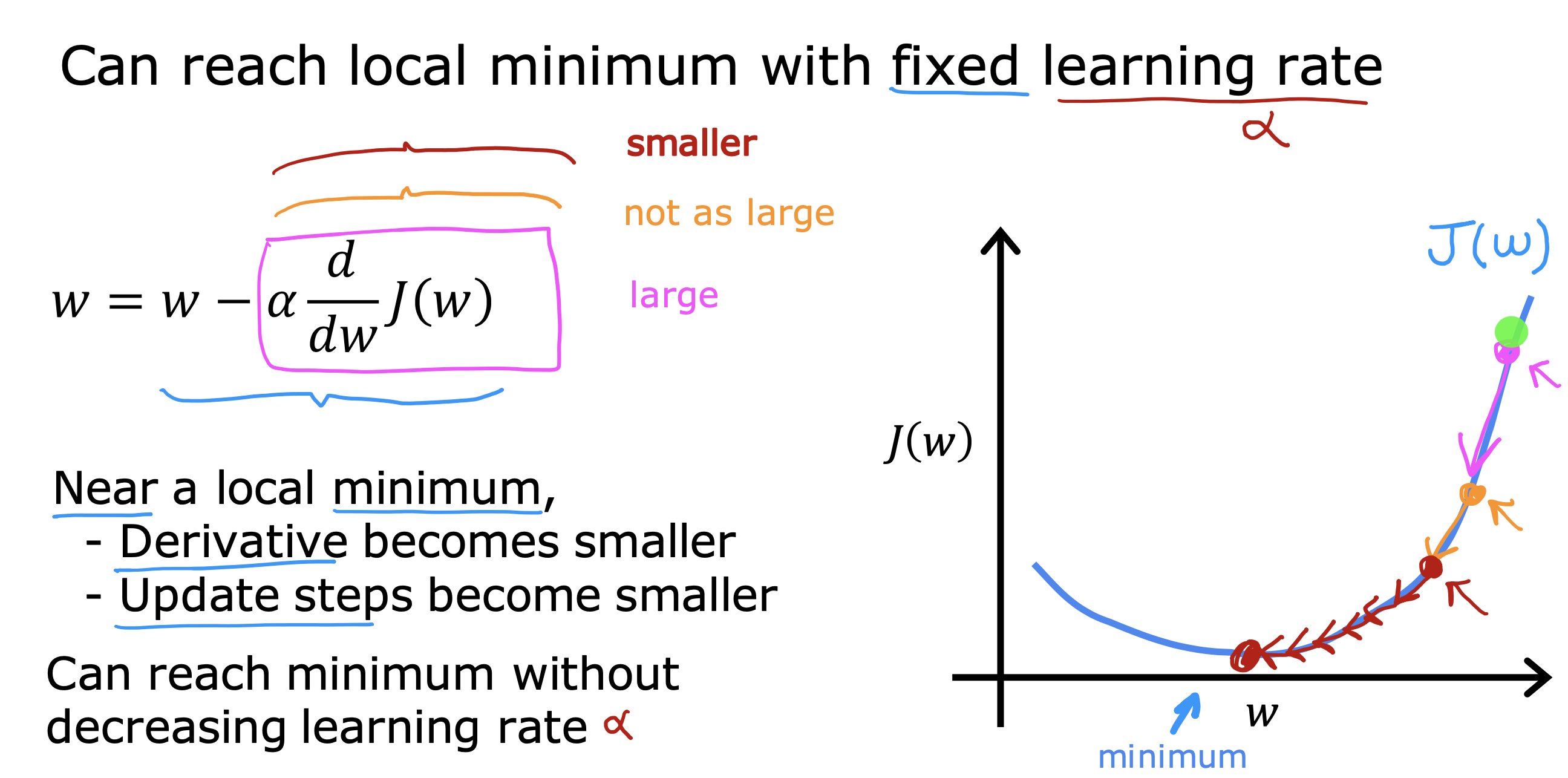
小结
线性回归模型,成本函数,和梯度下降算法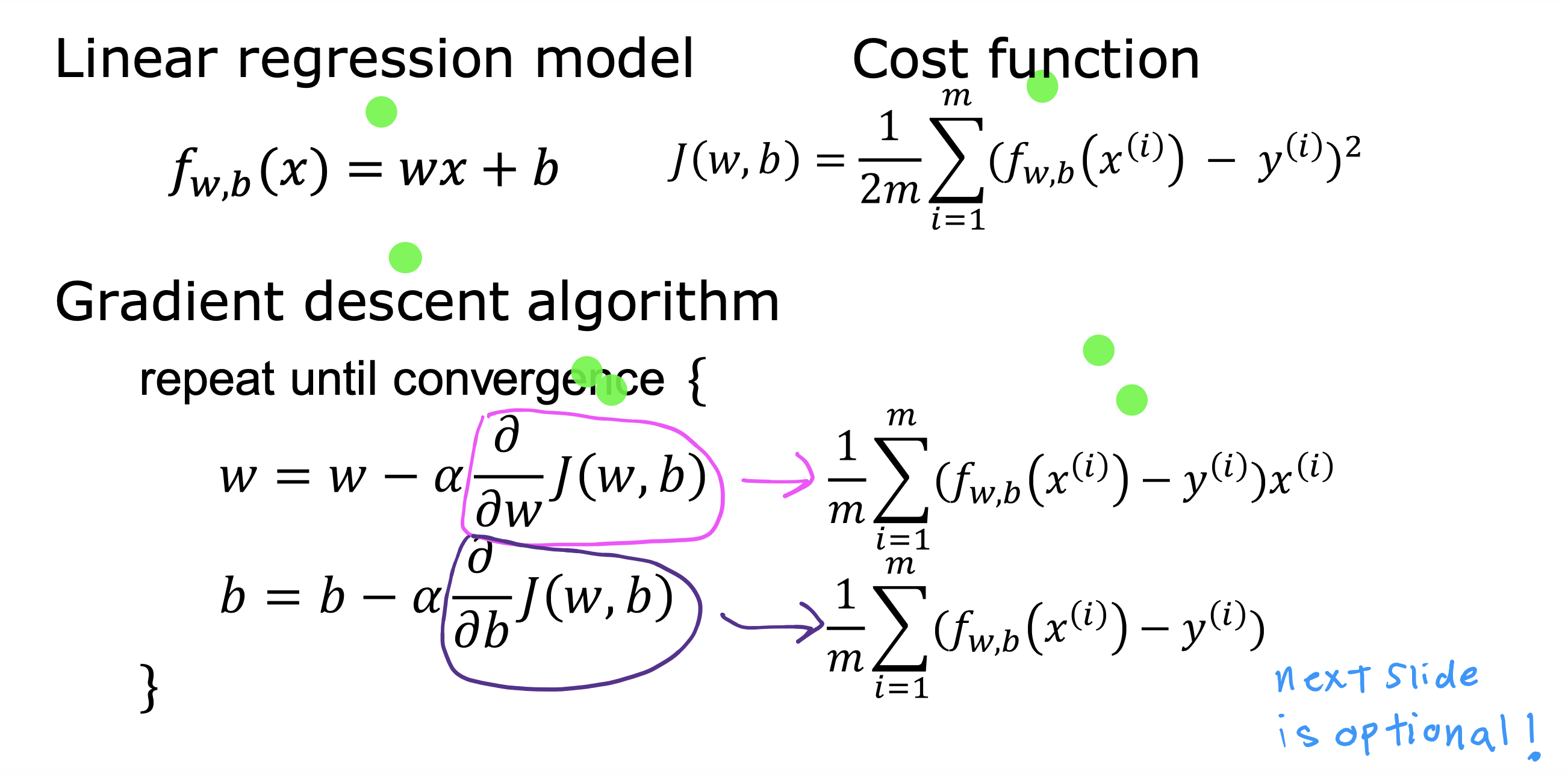
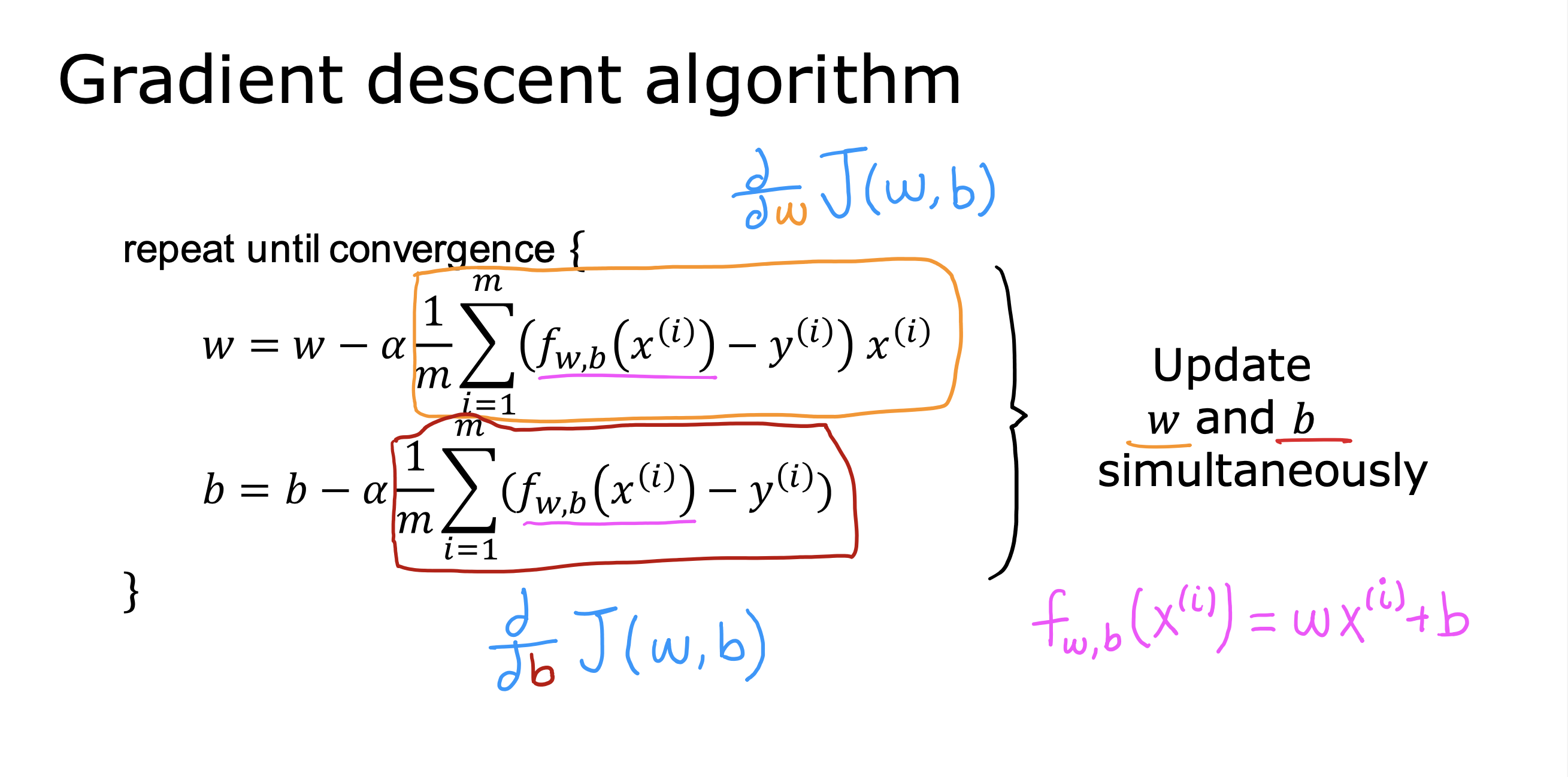
上述梯度下降算法具体来说是批量梯度下降,因为每一步都用到了所有训练数据
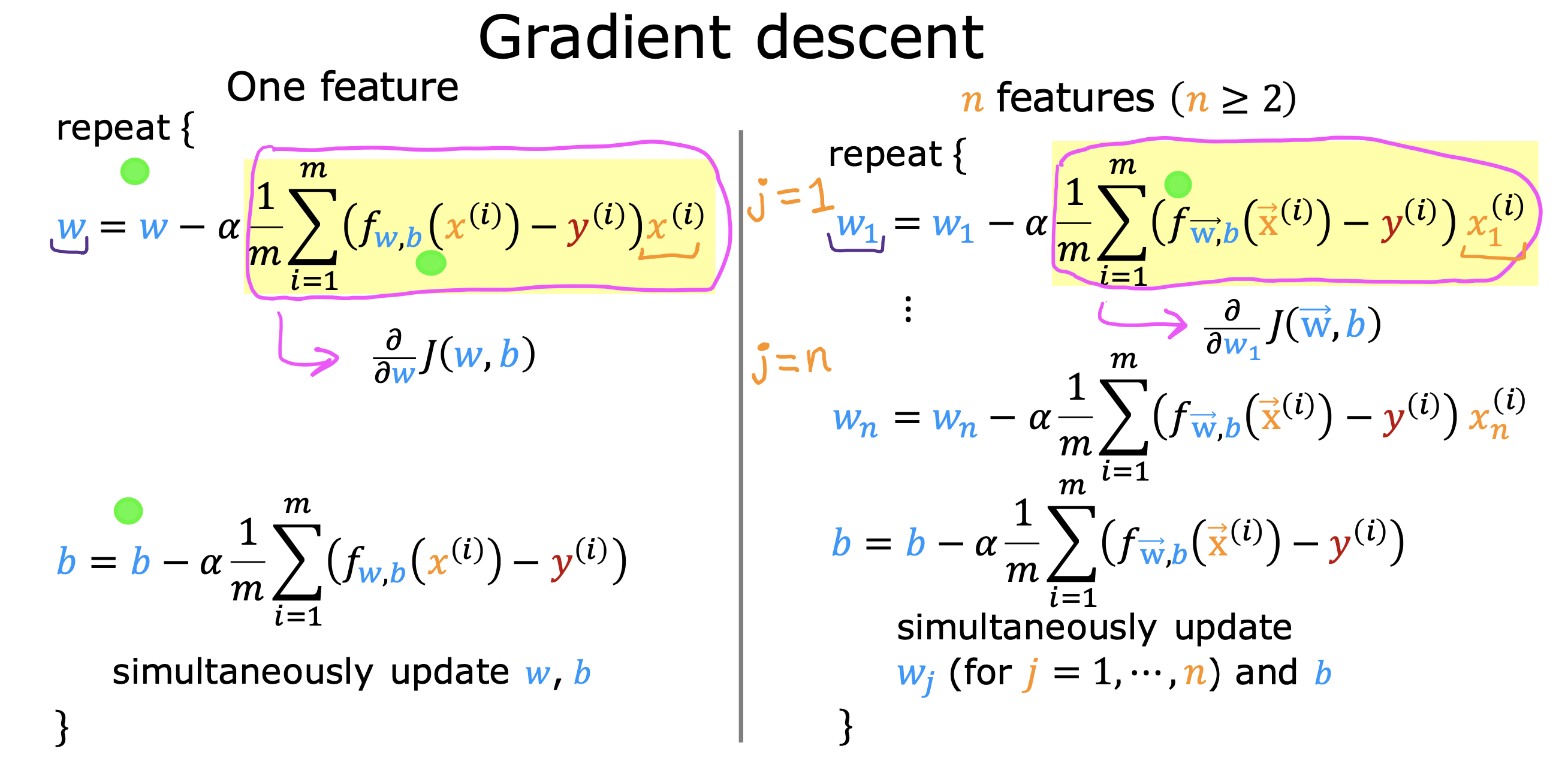
多元线性回归
以上讨论的是只有一个特征值x 作为输入的情况,下面要讨论的是同时有n个特征值做输入的模型,被称为多元线性回归模型
一些符号的表示方法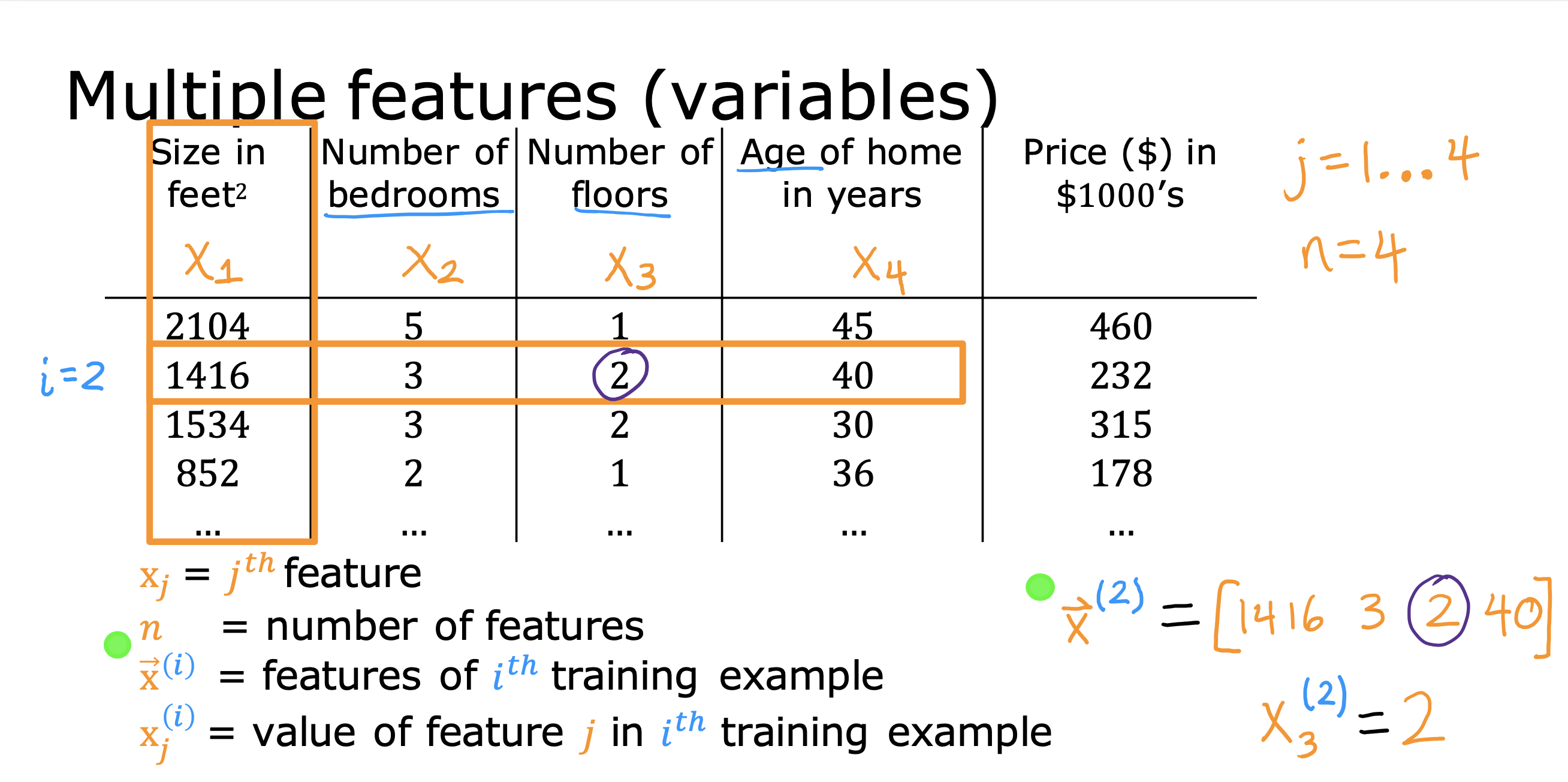
模型表达式
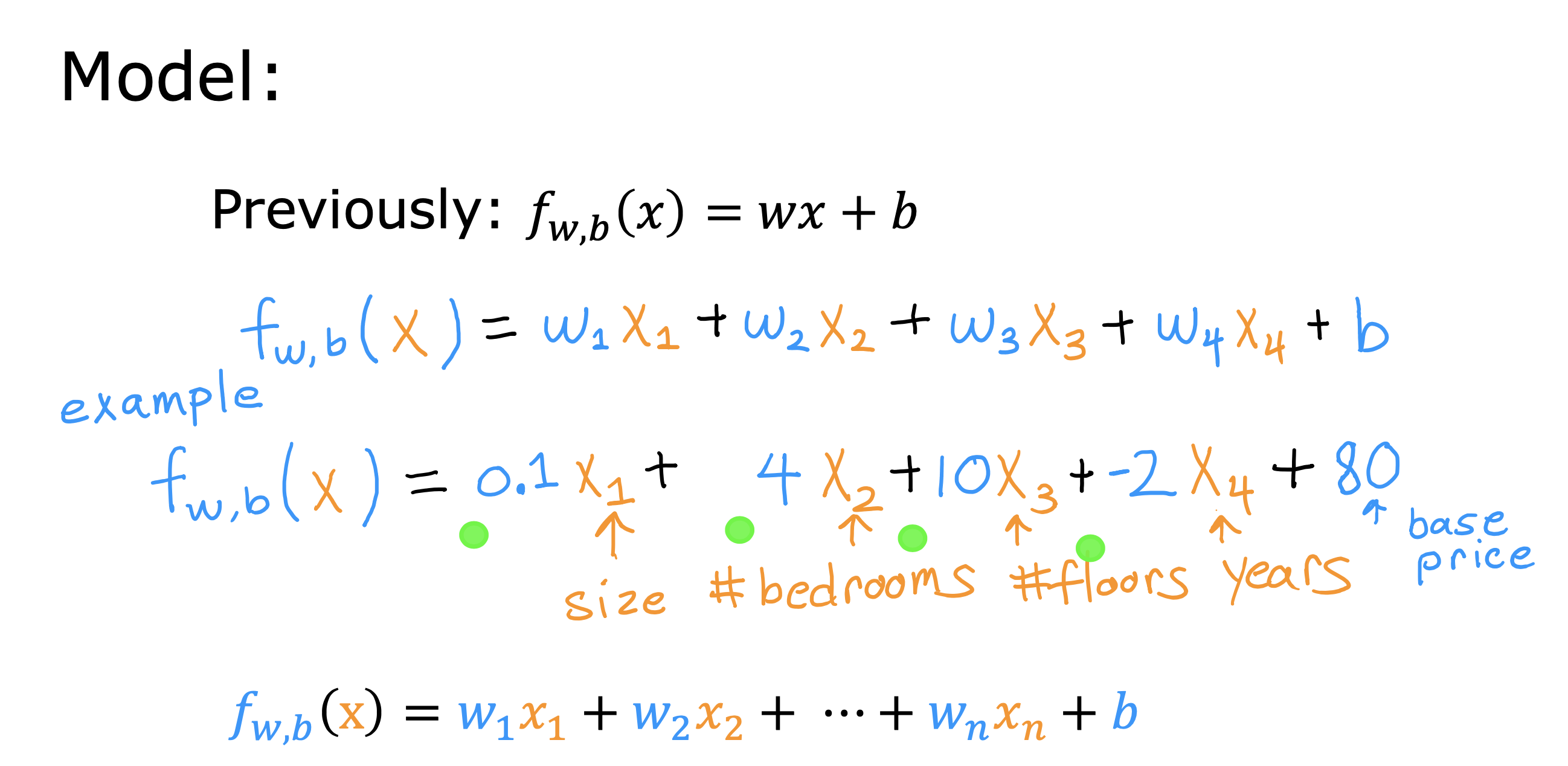
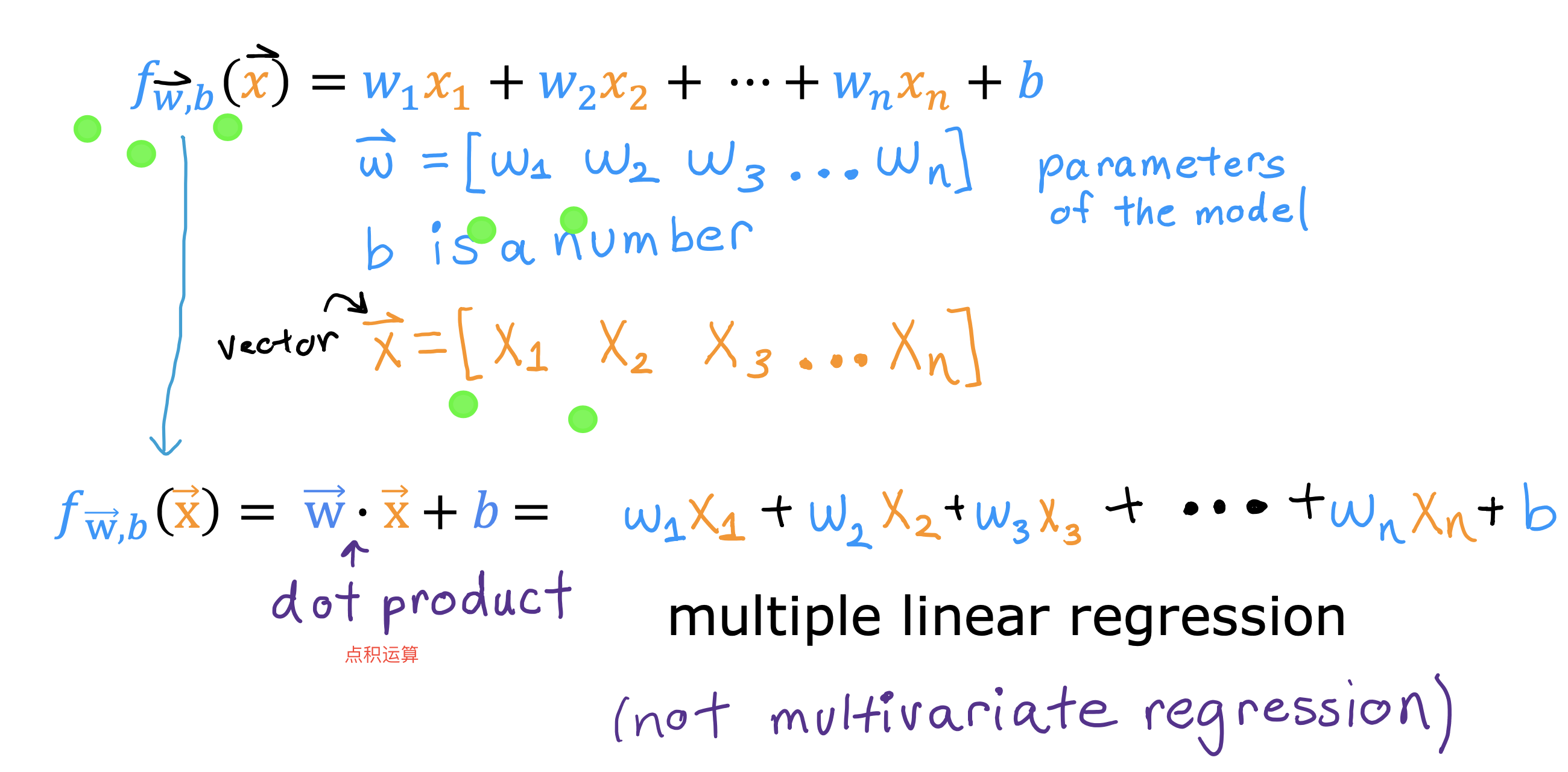
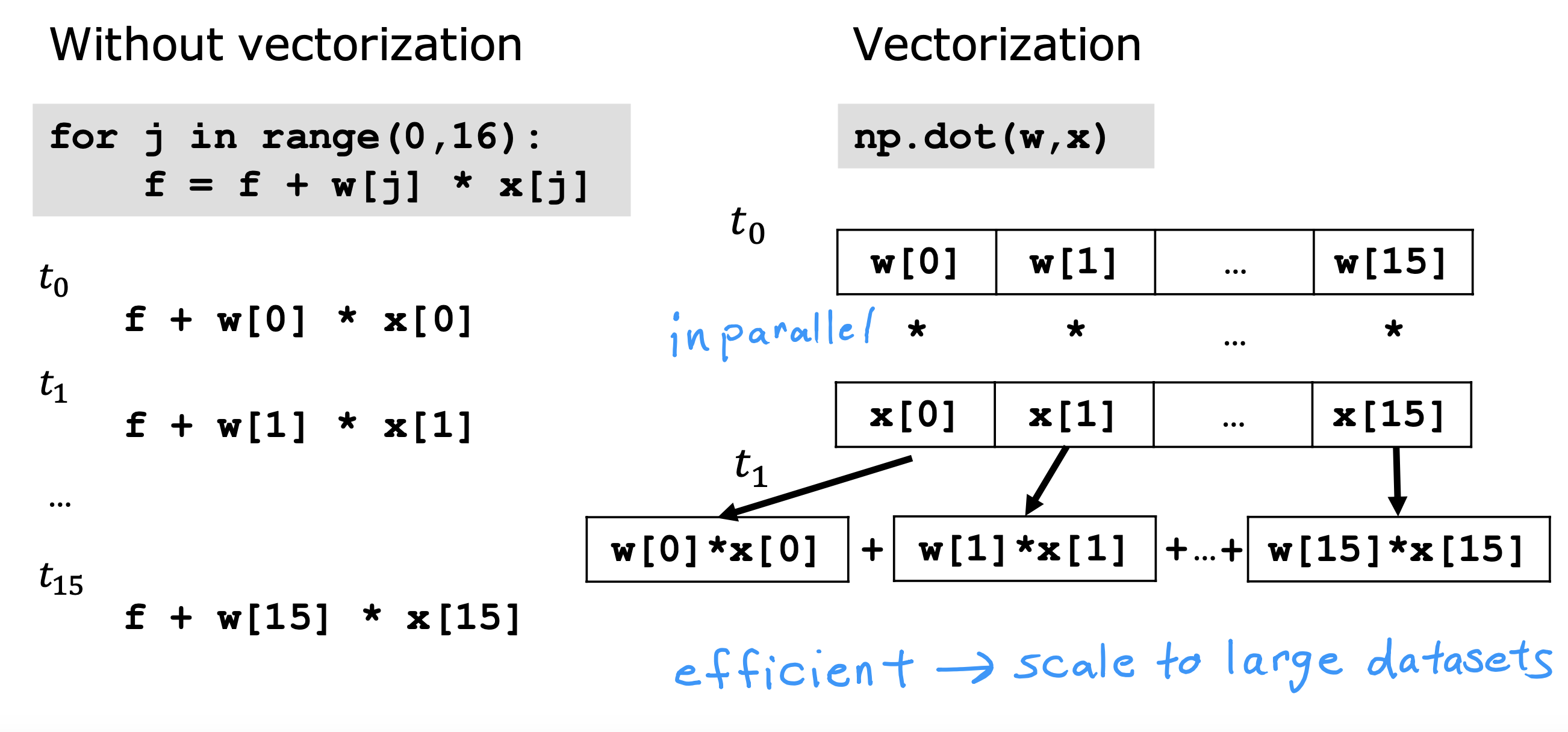
向量化
好处
- 代码实现简洁
- 运算速度快


对于多元线性回归 的 梯度下降算法
w 相关的计算转成向量计算,不同权重值,取对应特征值进行计算
实践技巧
如何更快的找到合适的参数去拟合训练集
特征缩放
参数大小与特征值大小关系
如果某一特征值(x1 属于[1000,5000]范围)相对其他特征值(x2,x3,..xn,属于[1,10]范围),数值范围较大,其对应参数w1 则相对其他较小
反之,如果特征值较小,则参数较大,这样的规律可以更快的找到适合的参数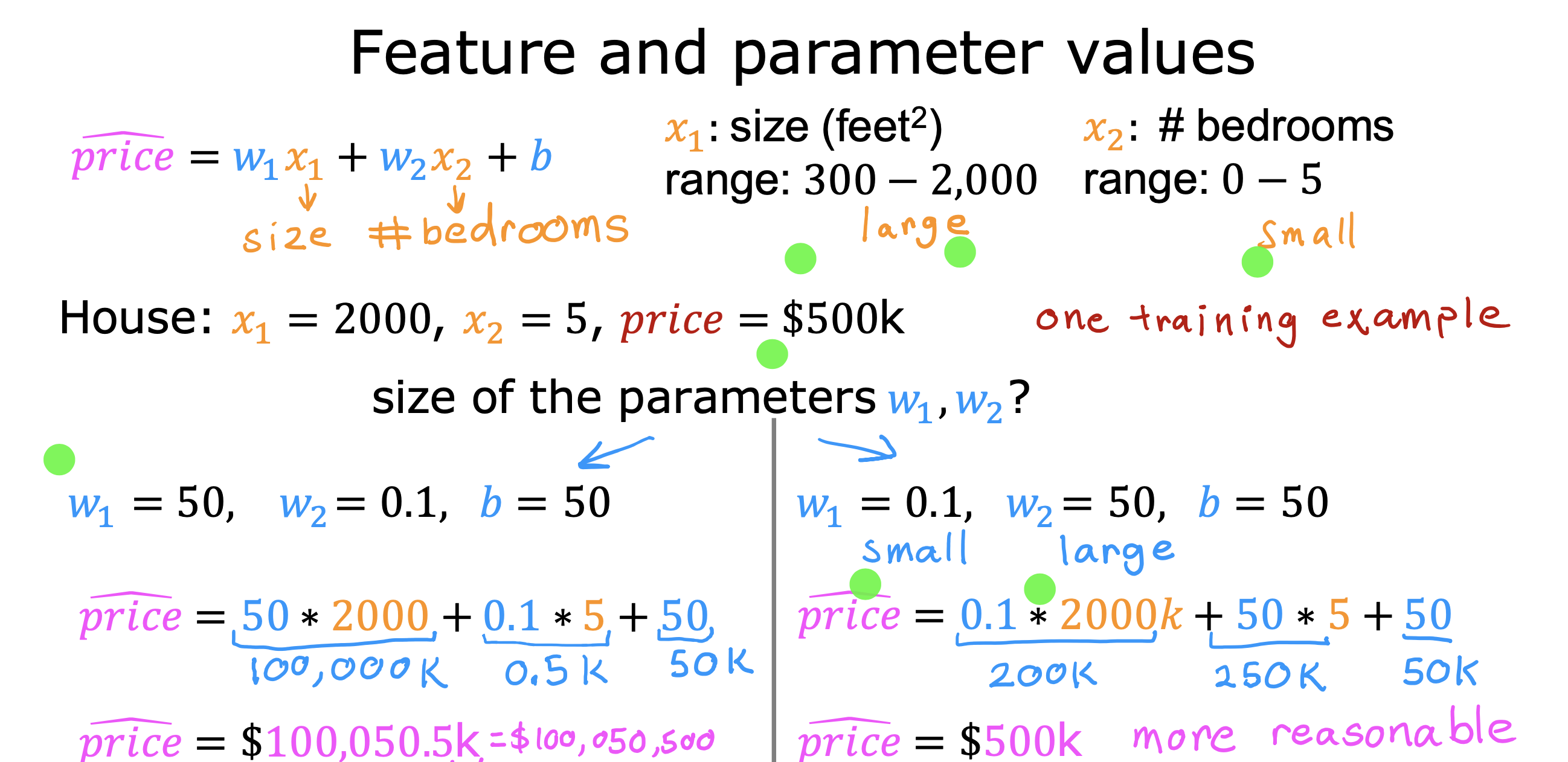
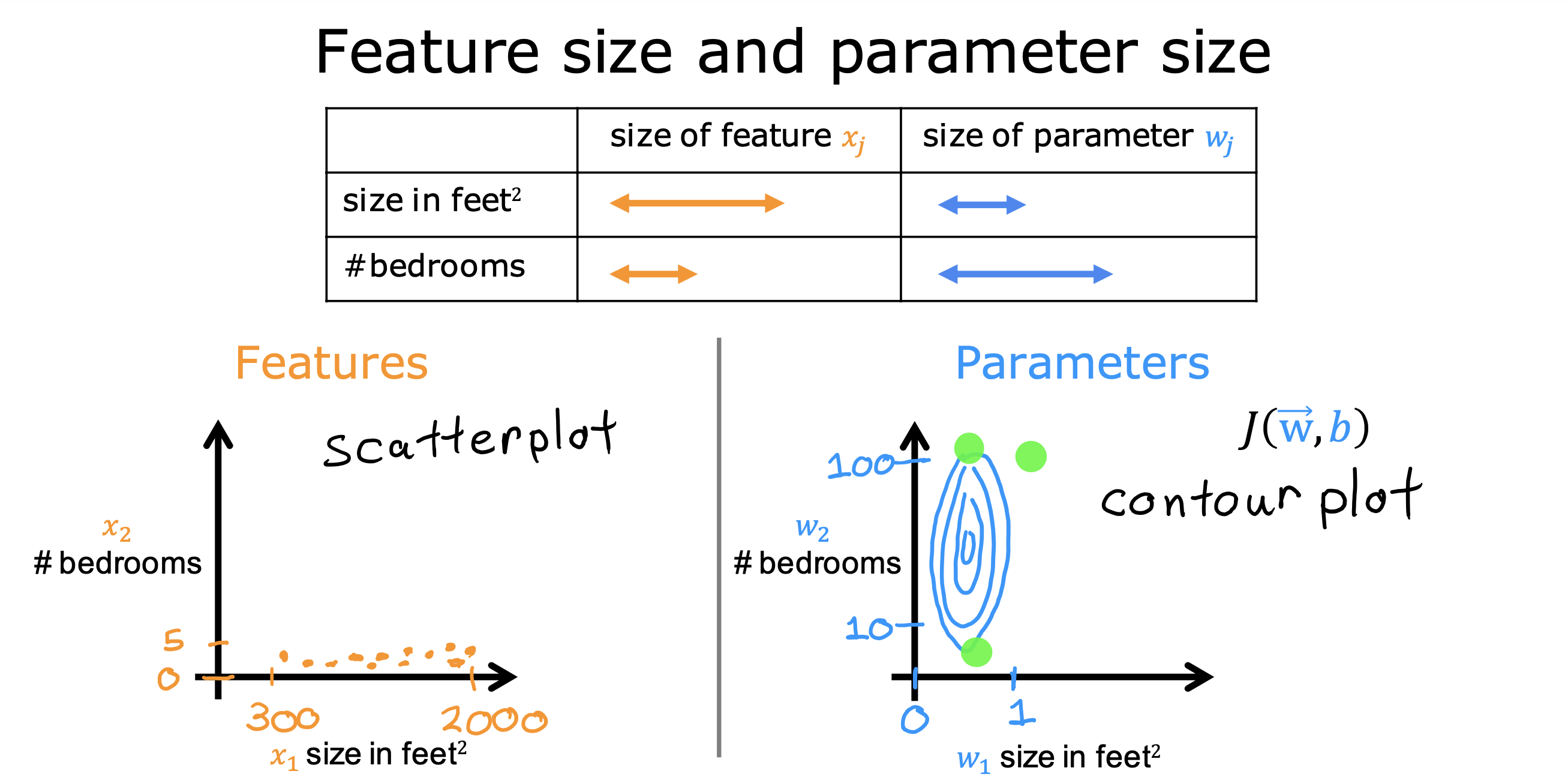
如果特征值的取值范围非常不同时,会导致梯度下降速度变慢
但如果将所有特征值想办法归一到相同的范围内,就可以加快梯度下降过程,降低计算步骤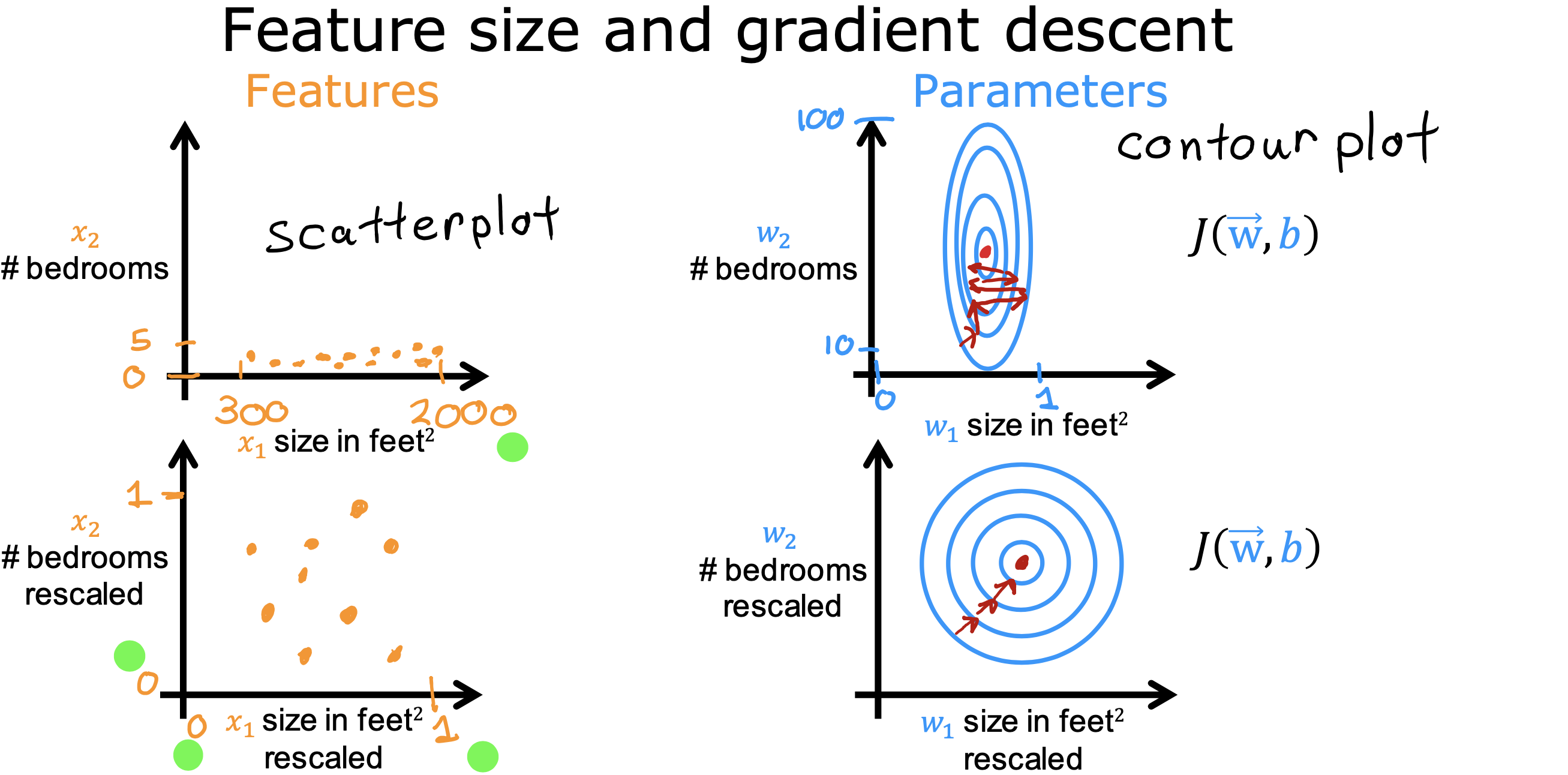
缩放计算方式
除以最大值
特征值除以各自范围的最大值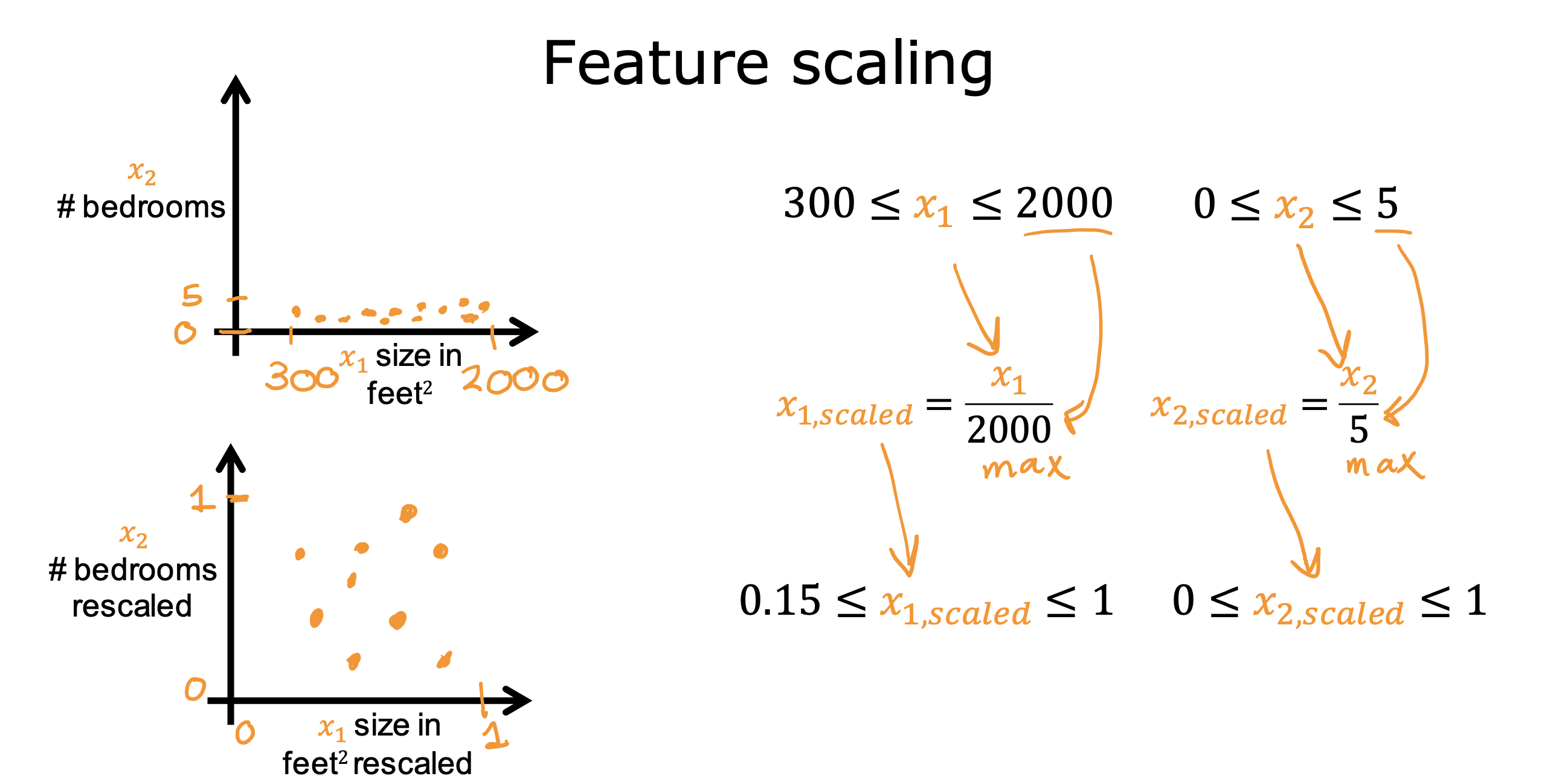
均值归一化
特征值 减去平均值,再除以极差值(范围最大值减去范围最小值)
Z-SCORE归一化
特征值 减去 标准差,除以 平均值
说明
并不一定非要落在-1 到1 之间,落在相同的数量级之间就可接受
如何找到成本函数最小值
学习曲线
绘制成本函数随迭代次数变化的趋势图,称为学习曲线,主要是根据曲线走势判断梯度是否在收敛
如果随迭代次数增加,成本函数一直呈下降趋势,说明梯度正在下降,是正常的
当下降到一定程度,随迭代次数成本函数不再有明显下降,说明梯度收敛到了极限,也就是找到了成本函数的最低点
但如果随次数增加,成本函数出现上升,这是不正常的,则说明学习率选取过大,需要重新选取,或者代码出现错误
自动收敛测试
自行定义一个极小的值,当某次迭代后成本函数值小于该值时,就认为梯度下降关闭,成本函数达到最小值,停止迭代,取当前迭代wb做模型参数
缺点就是极小值难以估计,且结果不太可靠
如何选择合适学习率
根据学习曲线调整学习率
学习率太大会导致学习曲线出现上升趋势
太小会导致迭代次数增加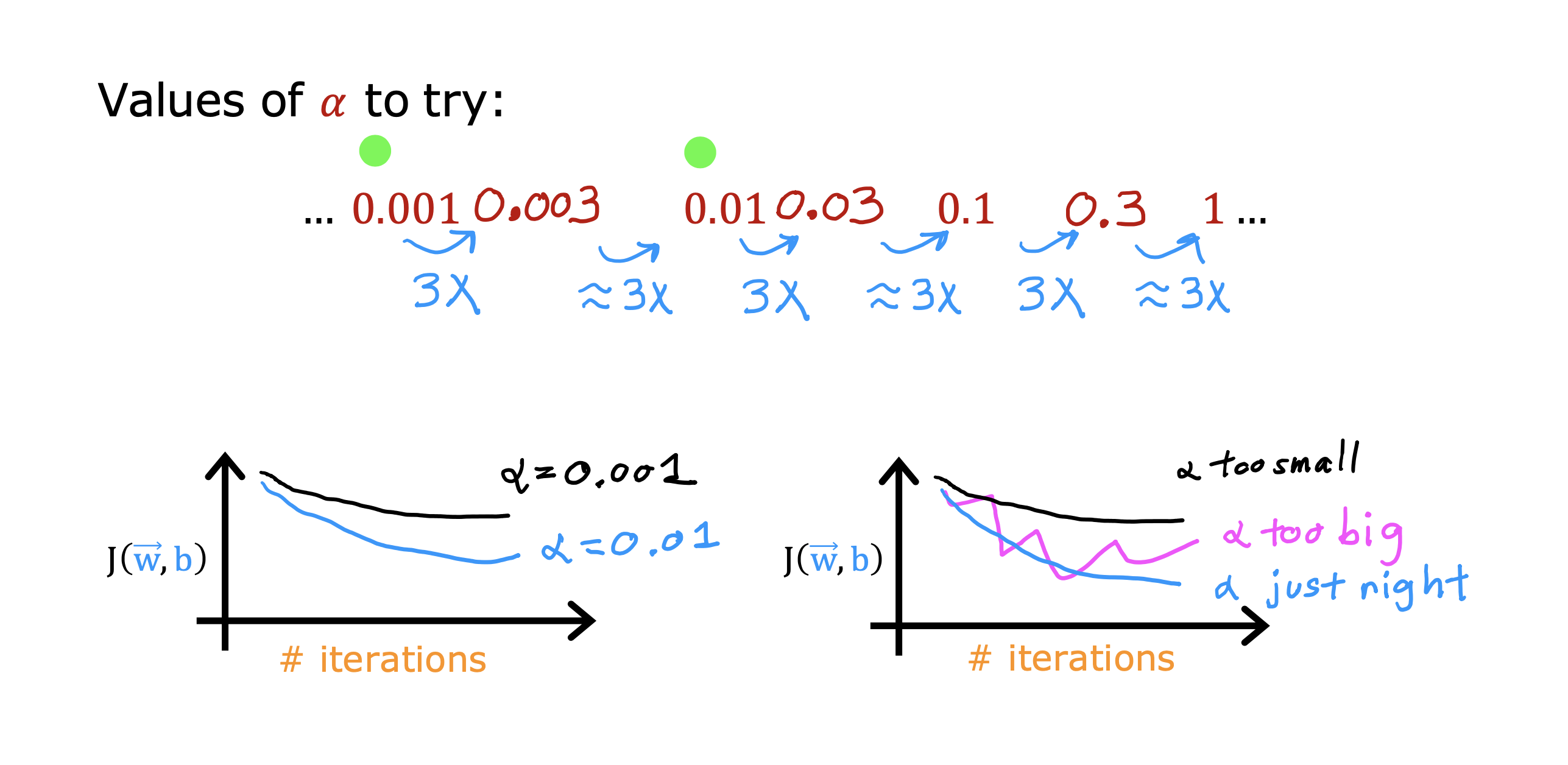
可以先对不同量级的学习率进行测试,观察学习曲线变化快慢
然后进行N倍测试,再比较,通过多组测试观察学习曲线变化快慢进行选取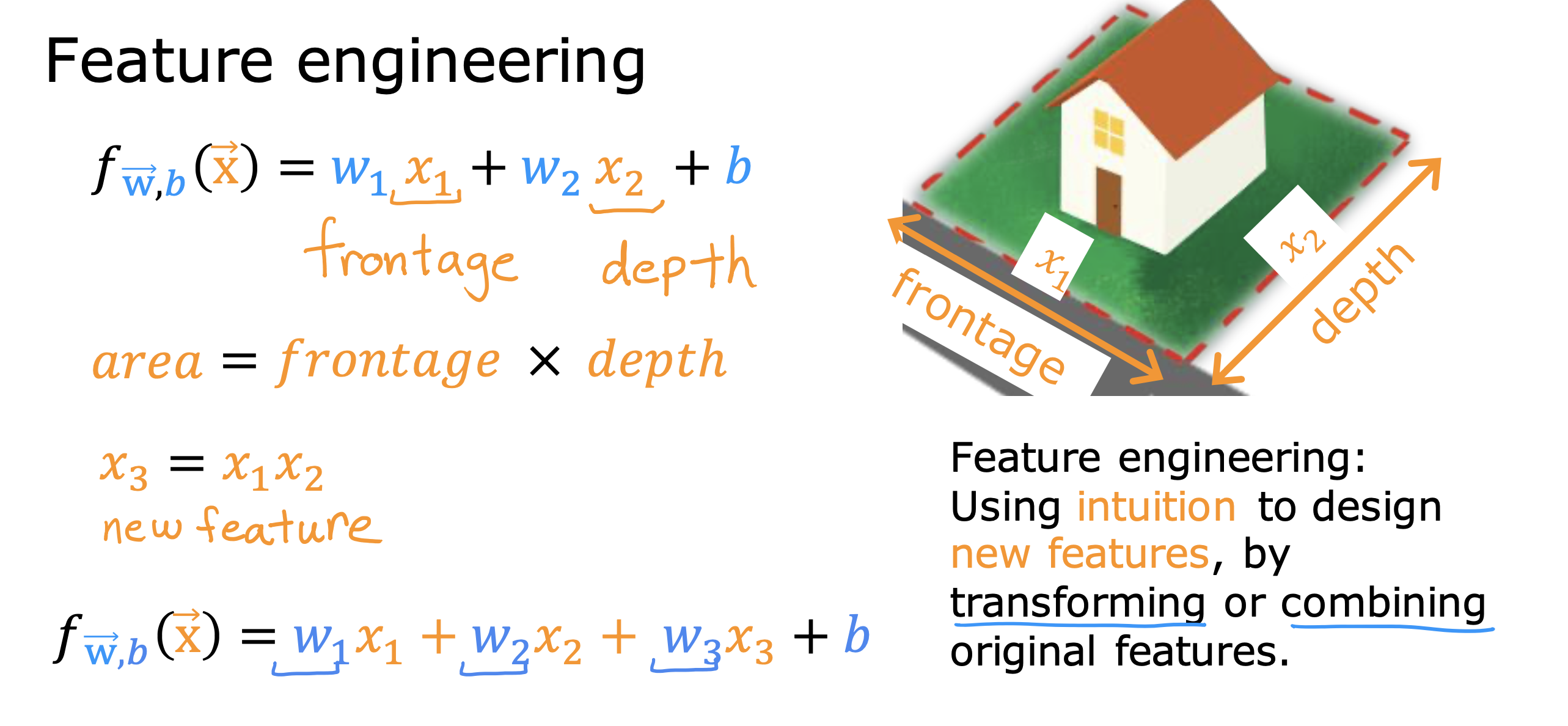
特征工程
通过转换或者合并直接(原始)的特征值,生成新的特征值进行模型训练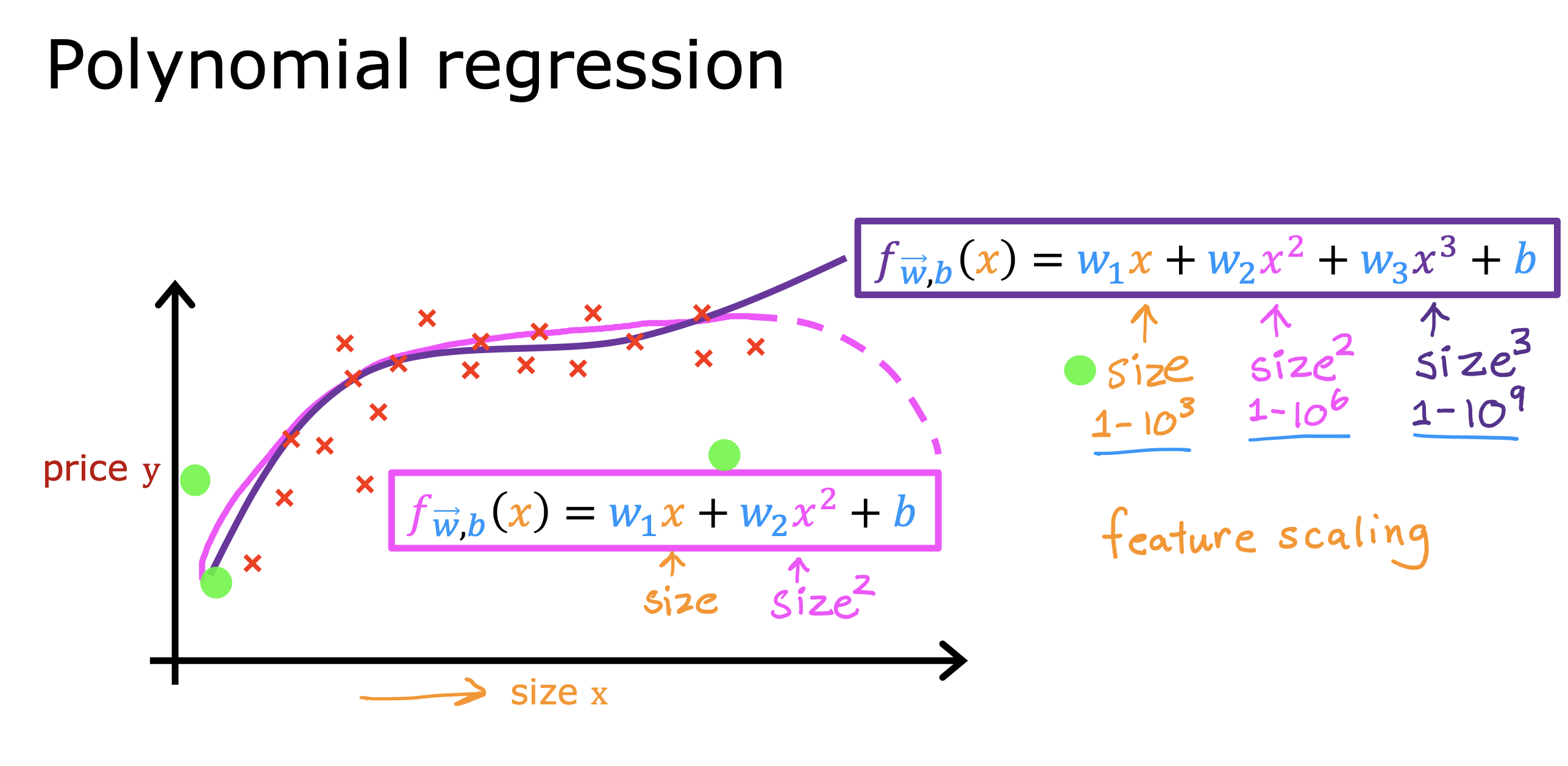
多项式回归
如果特征值只有一个的情况下,不希望得到线性回归的直线模型,希望用曲线去拟合训练集
可以采用下面两种方法去拟合
- 通乘方构建新特征值,但是在进行训练时要进行归一化处理,因为乘方处理后,各个特质值范围的数量级会变得不同
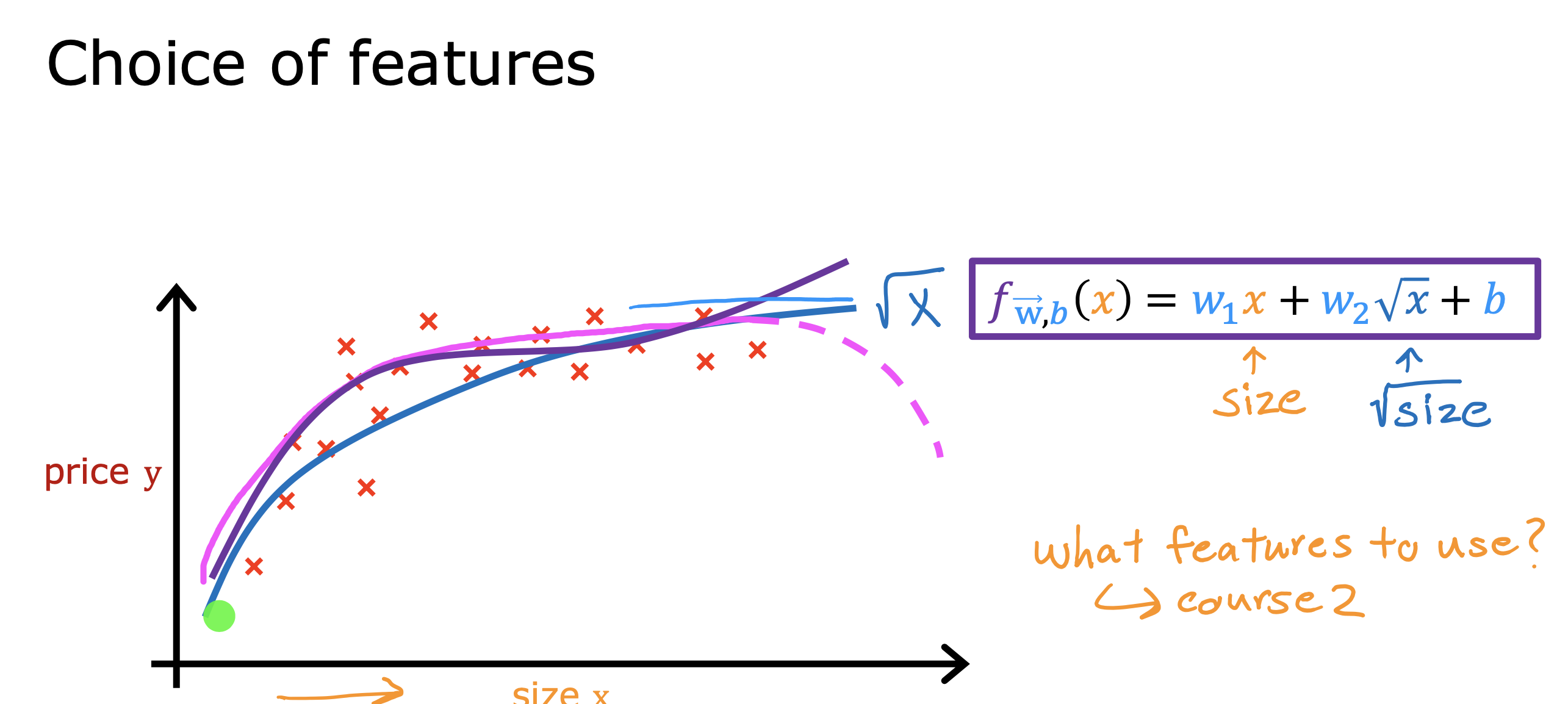
- 通过开方进行新特征值构建
如何在colab中运行github 上的jupiter文件
下面这个链接时梯度下降实现的.ipynb 文件
复制域名之后的path
kaieye/2022-Machine-Learning-Specialization/blob/main/
Supervised%20Machine%20Learning%20Regression%20and%20Classification/week1/work/C1_W1_Lab05_Gradient_Descent_Soln.ipynb
拼接到 https://colab.research.google.com/github/ 后面
得到访问链接
如果.ipynb有依赖其他py 文件,可以点击上传图标直接上传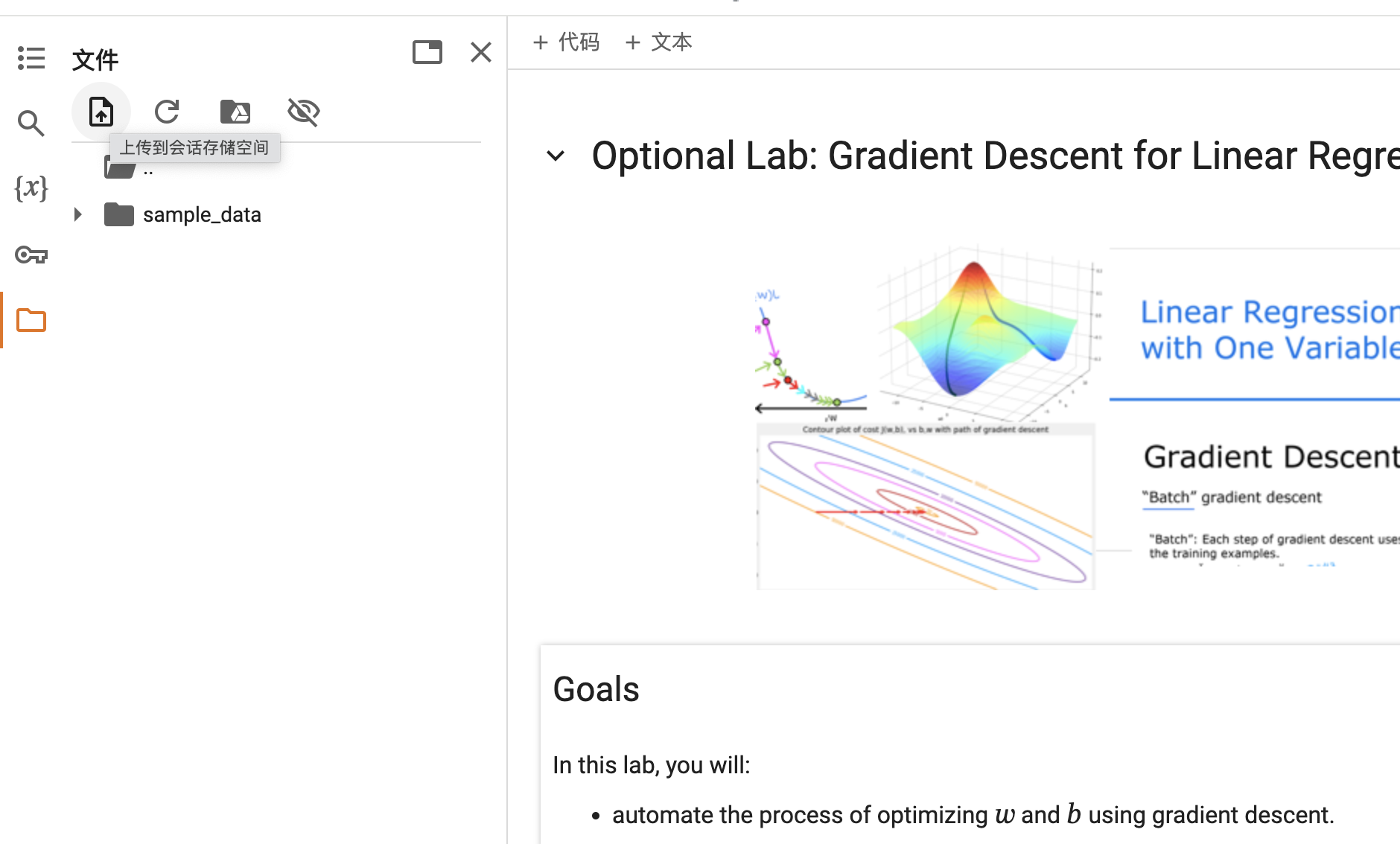
但是要注意这里上传的文件都是运行时的状态,页面关闭即销毁,
如果想要保存自己修改后的.ipynb文件可以通过添加副本到google/drive 来实现