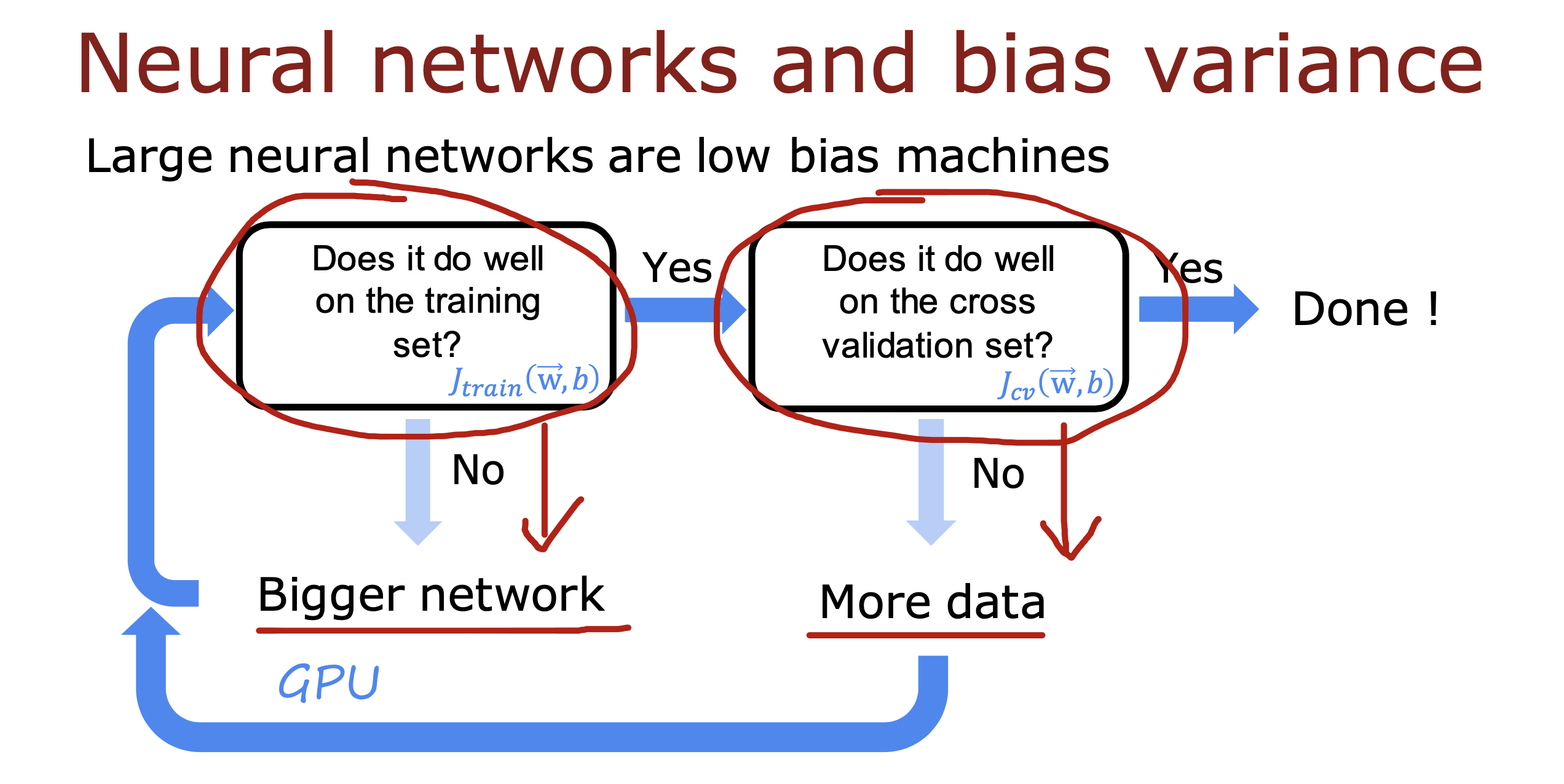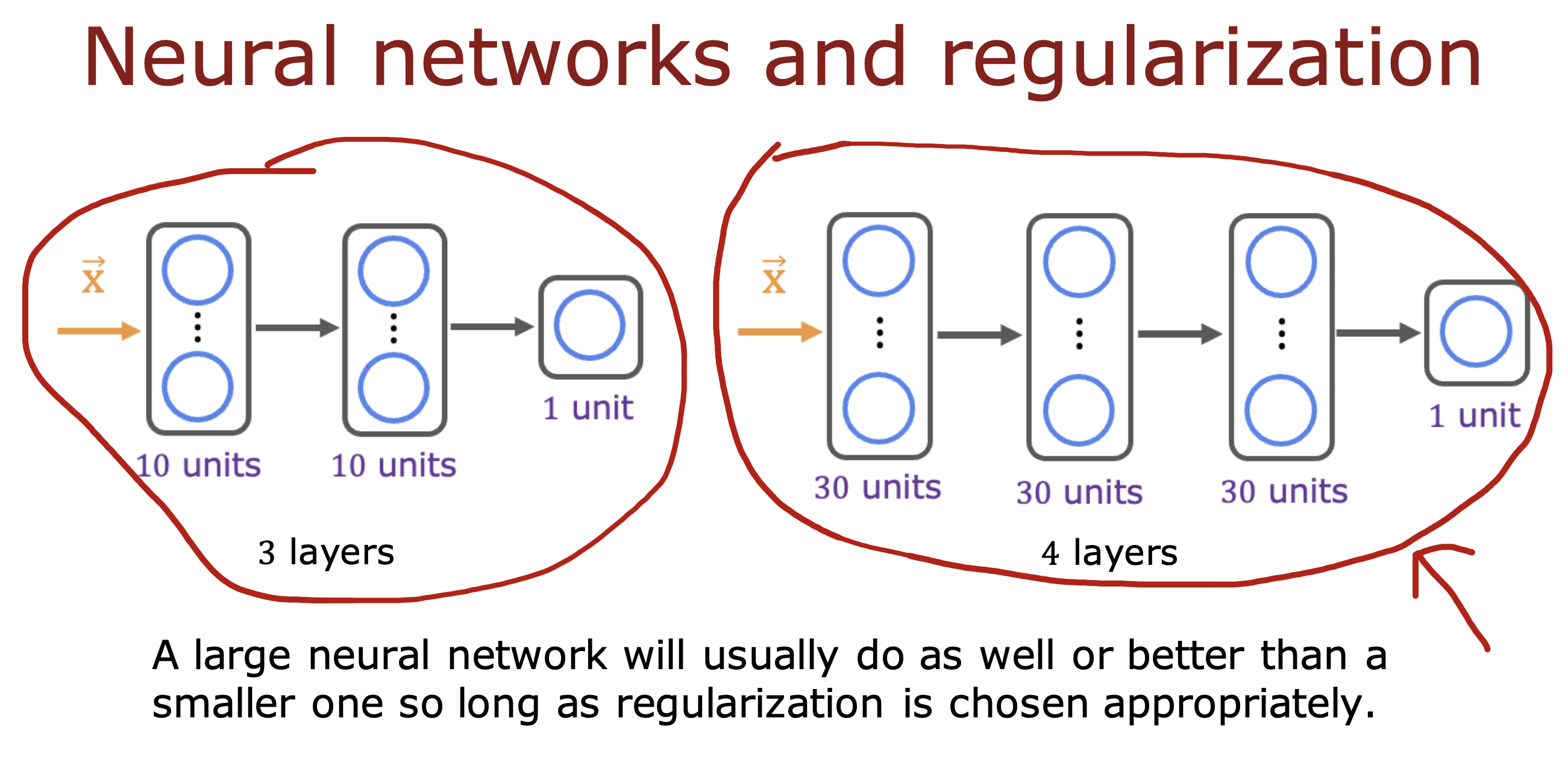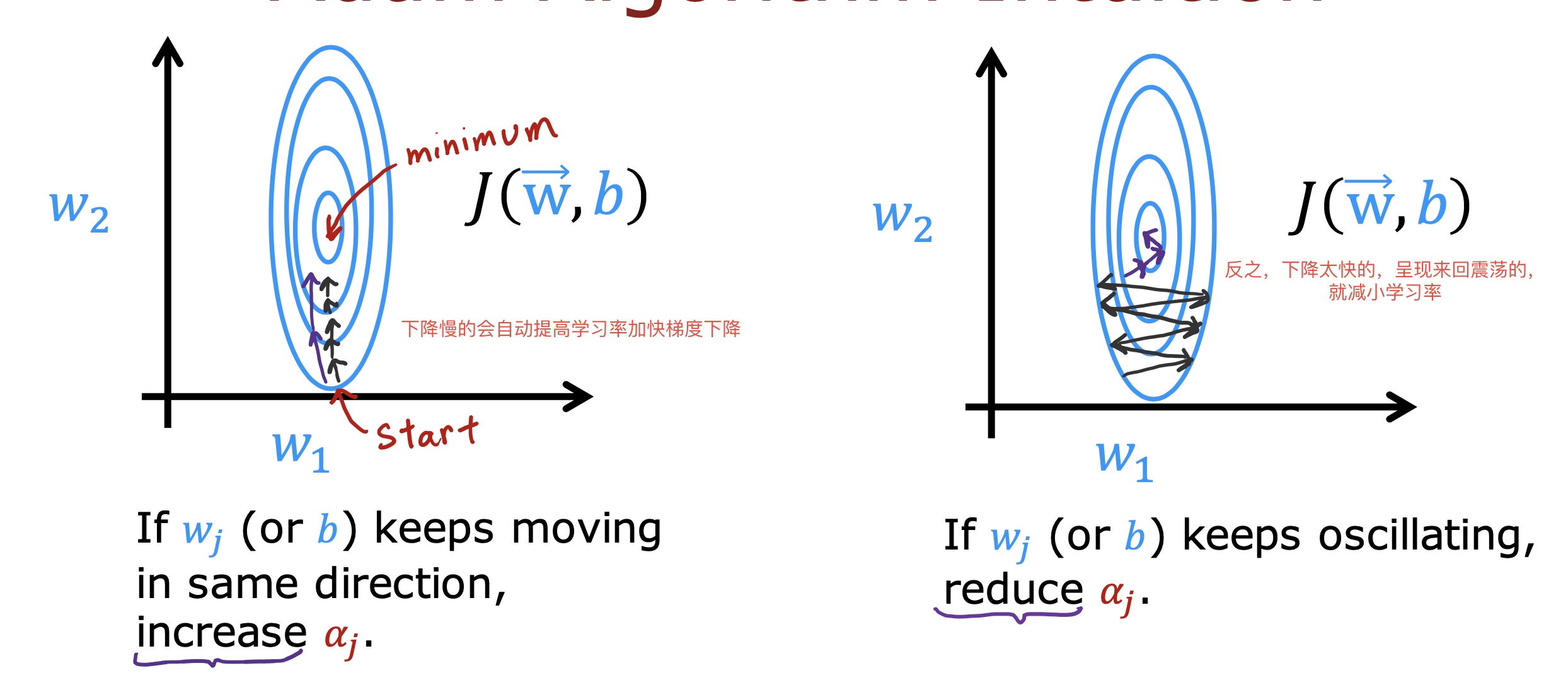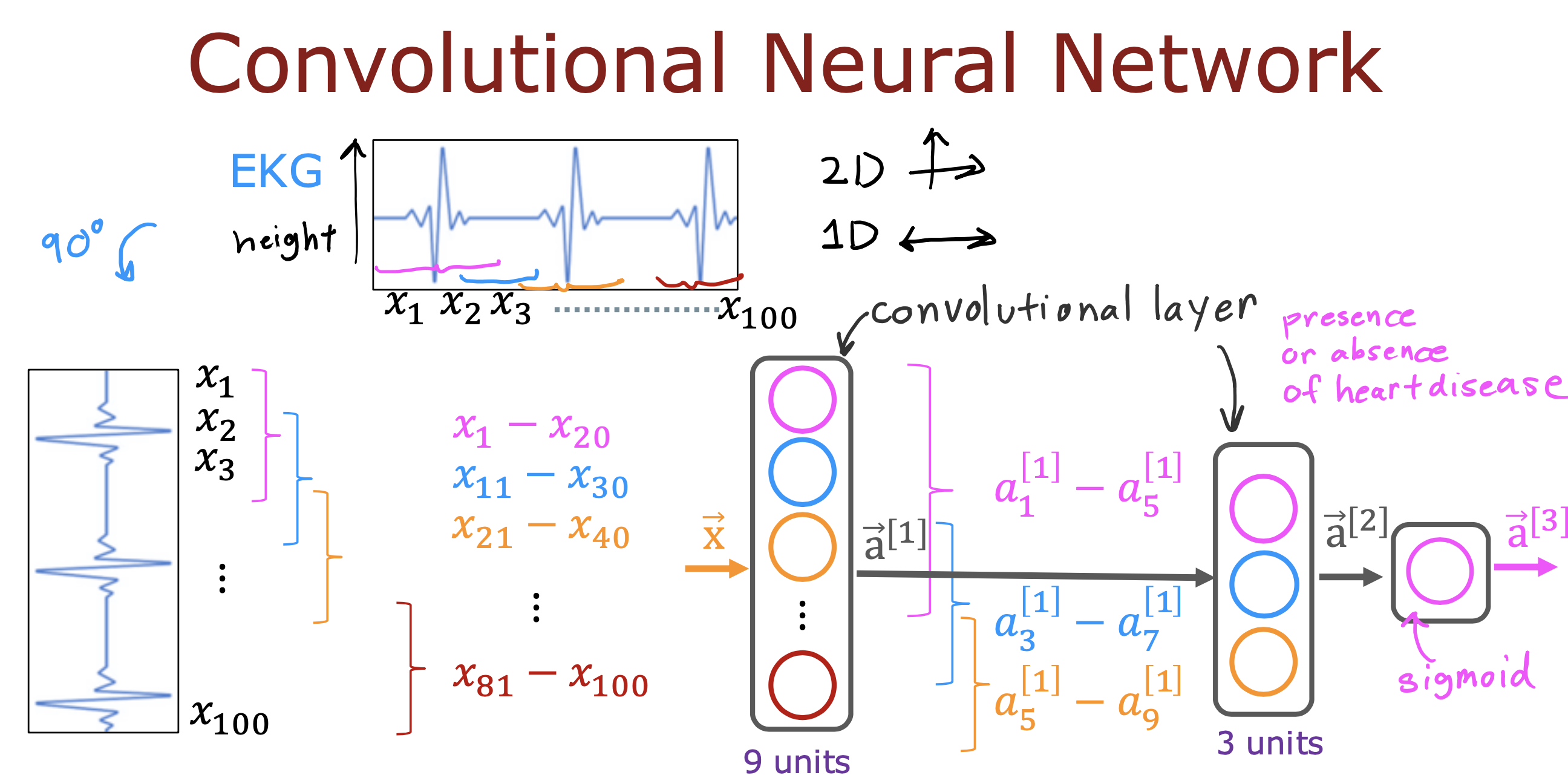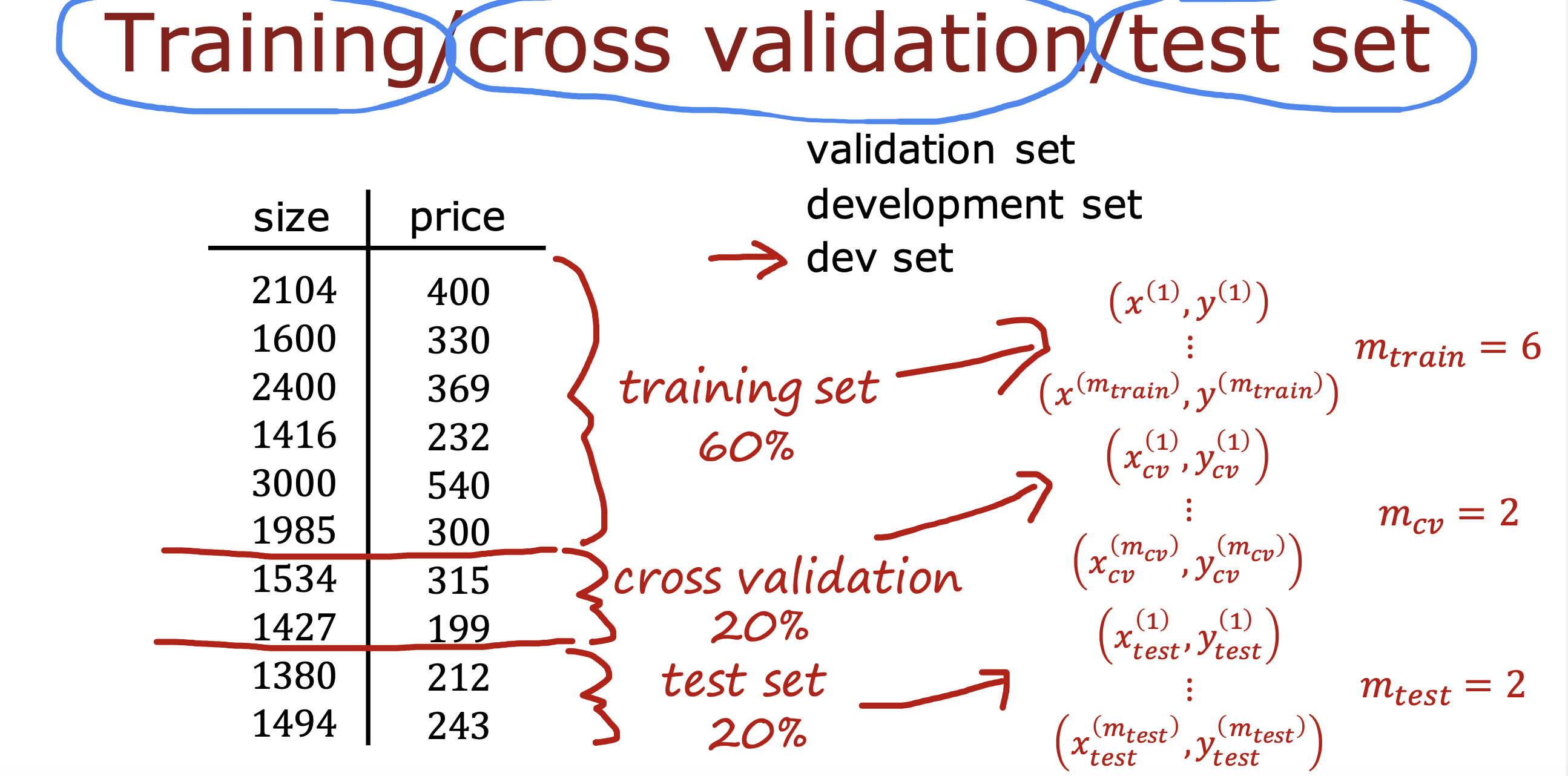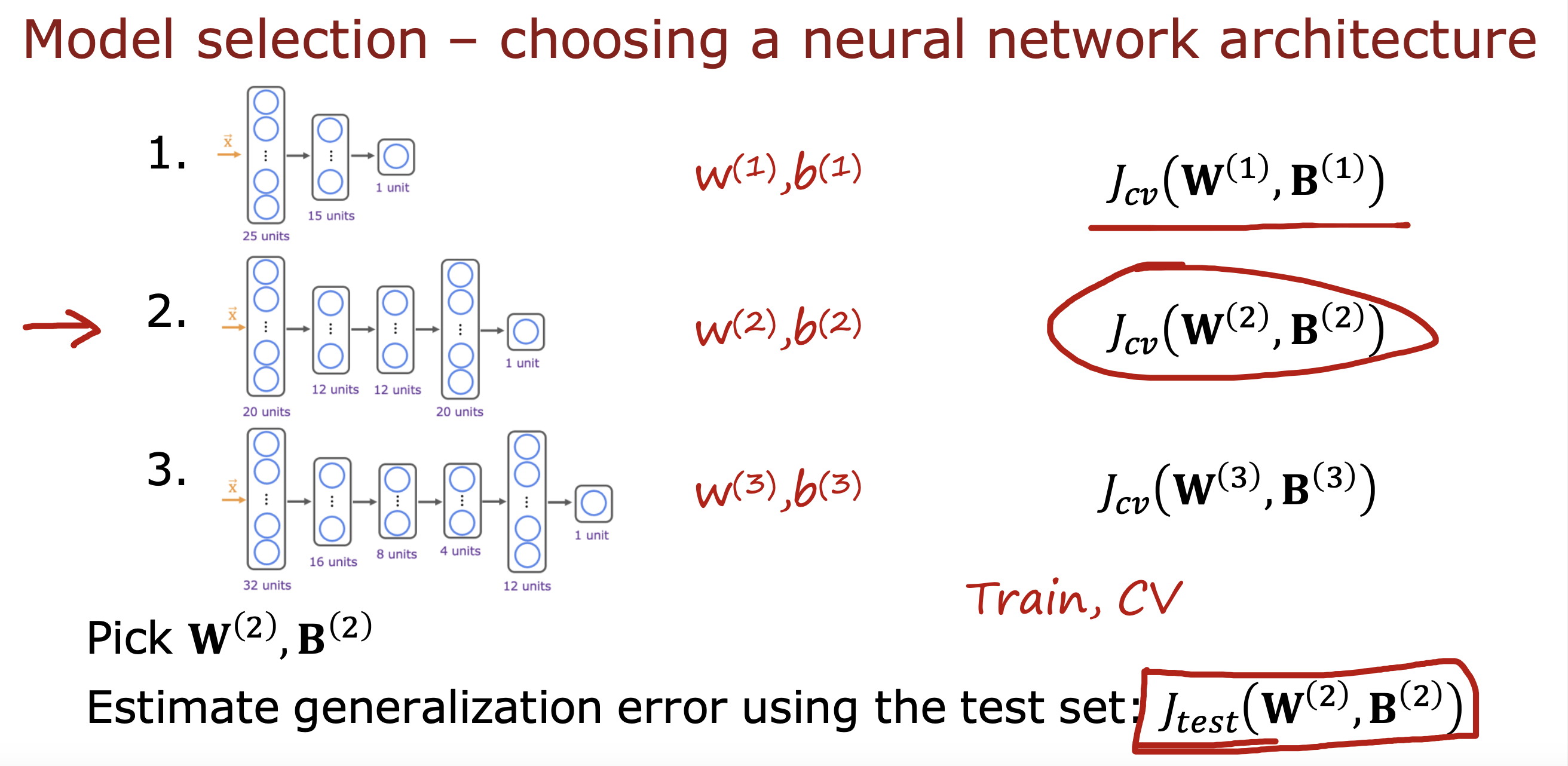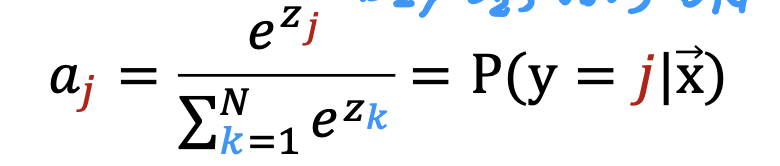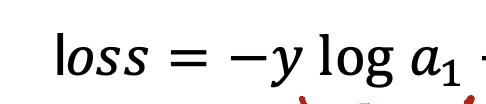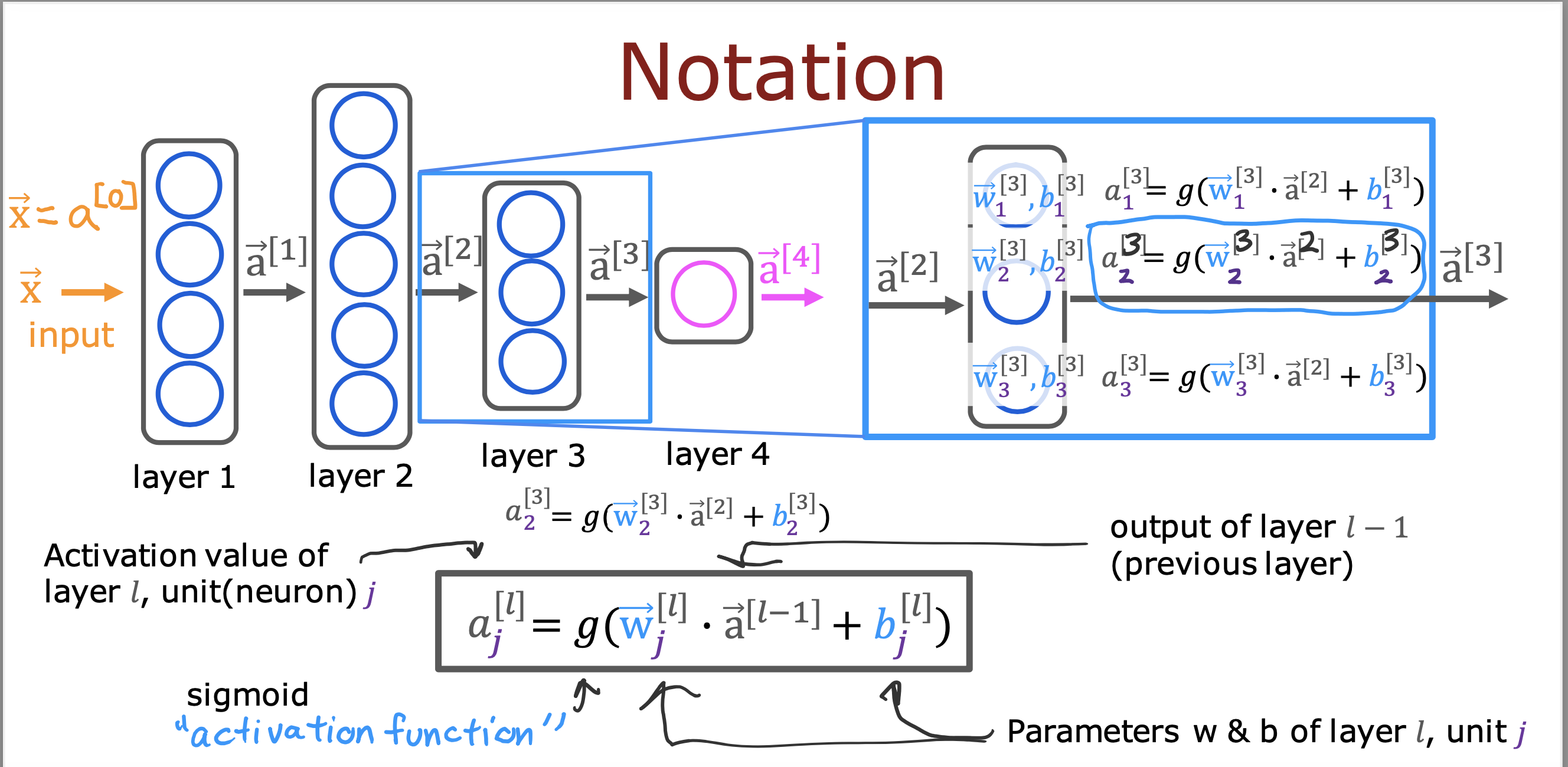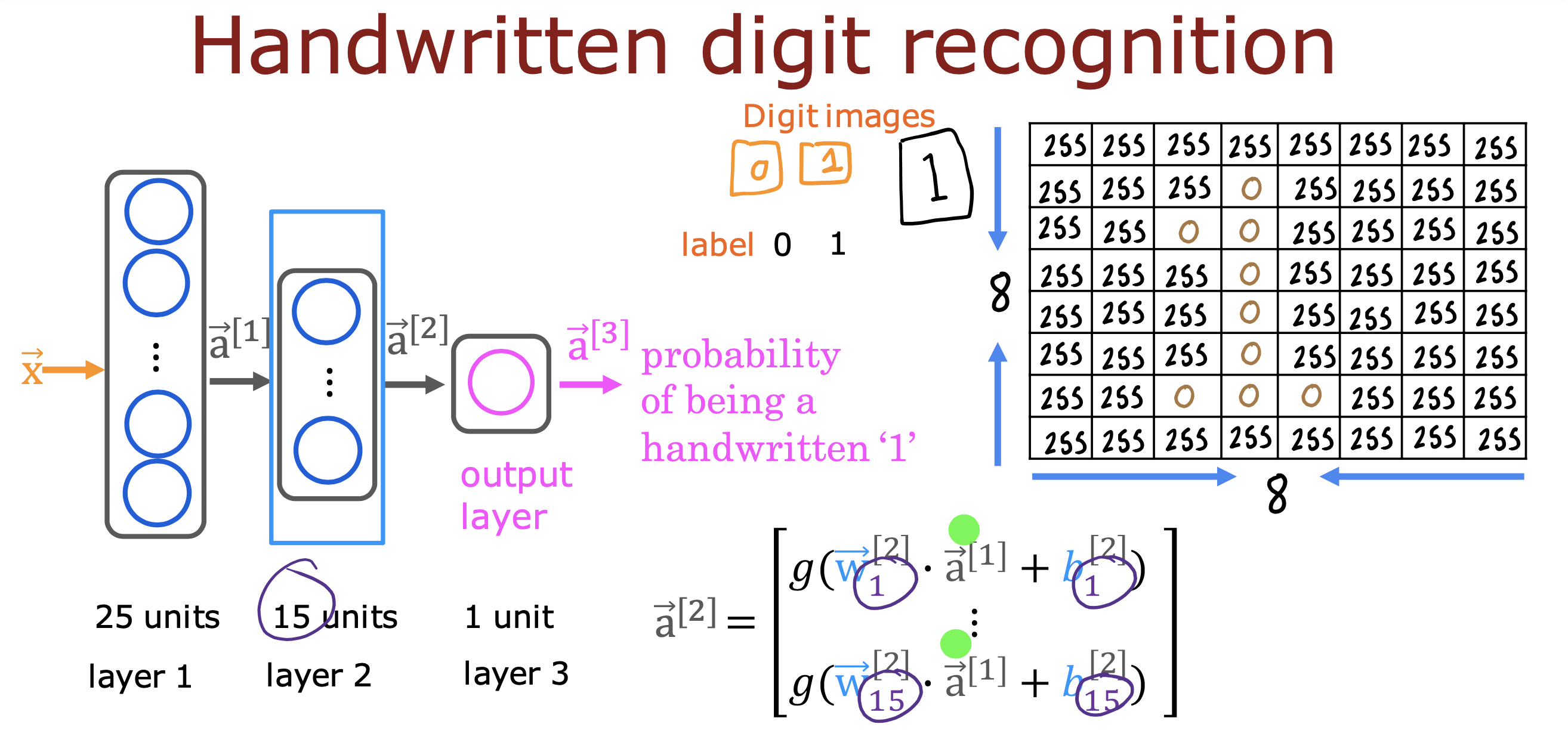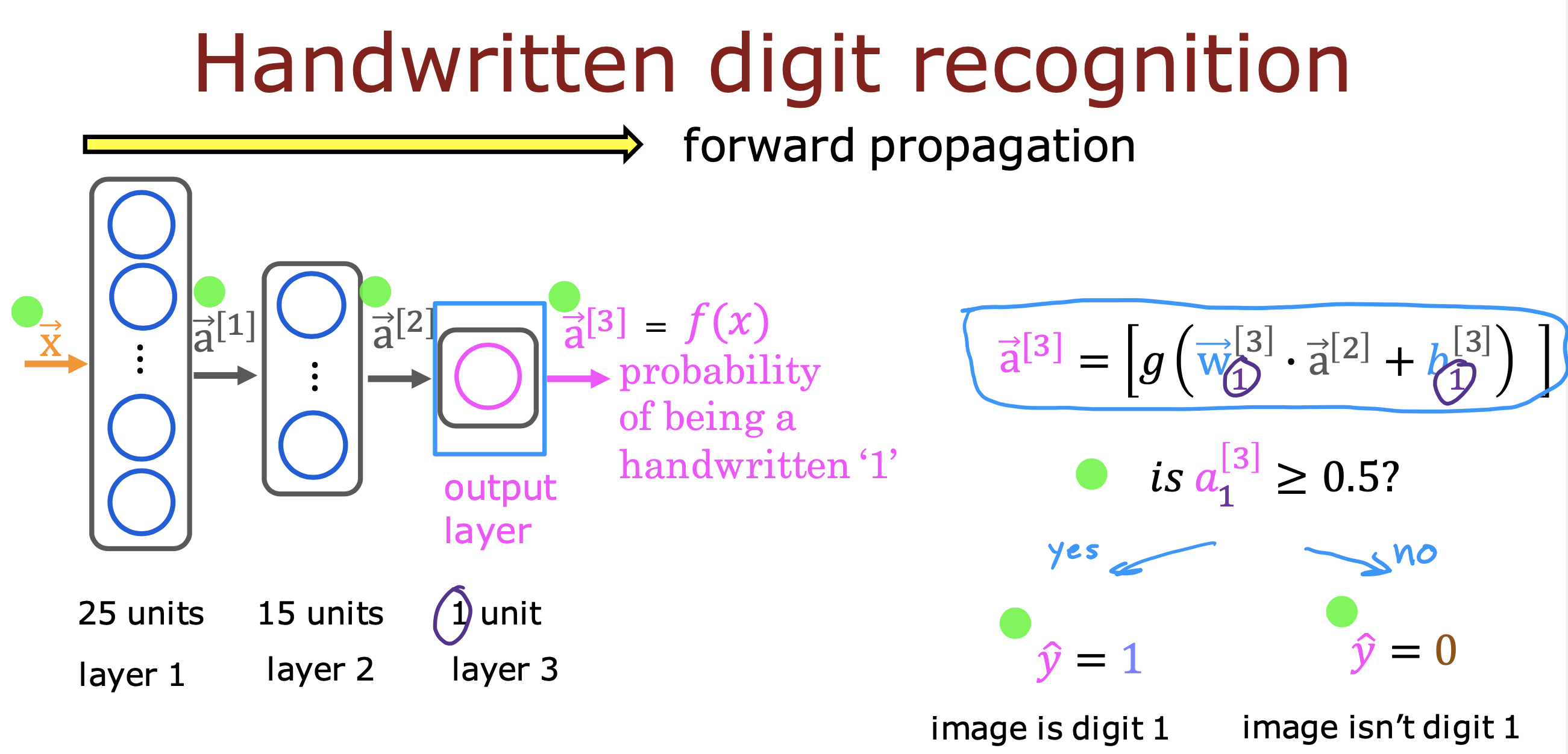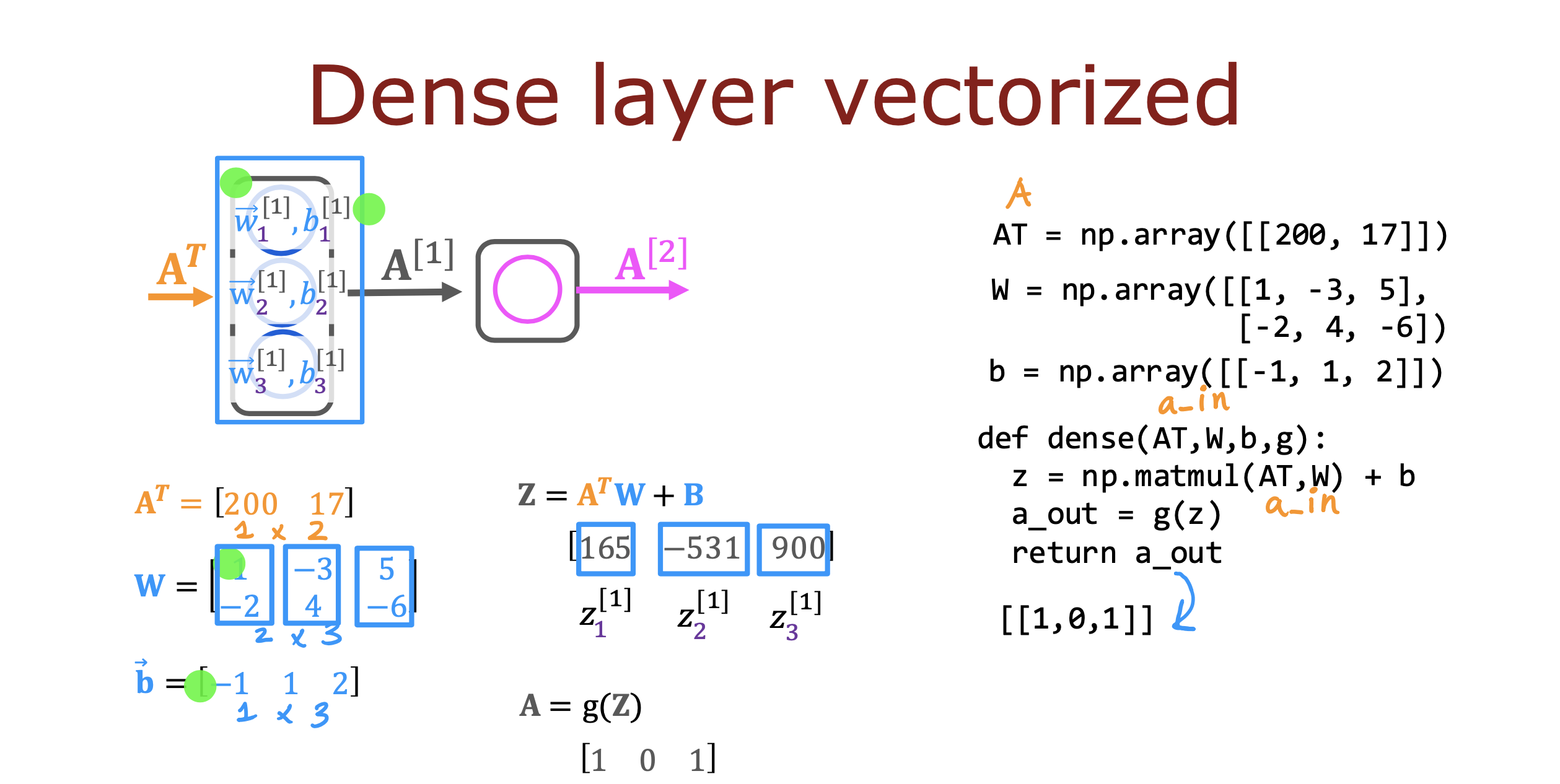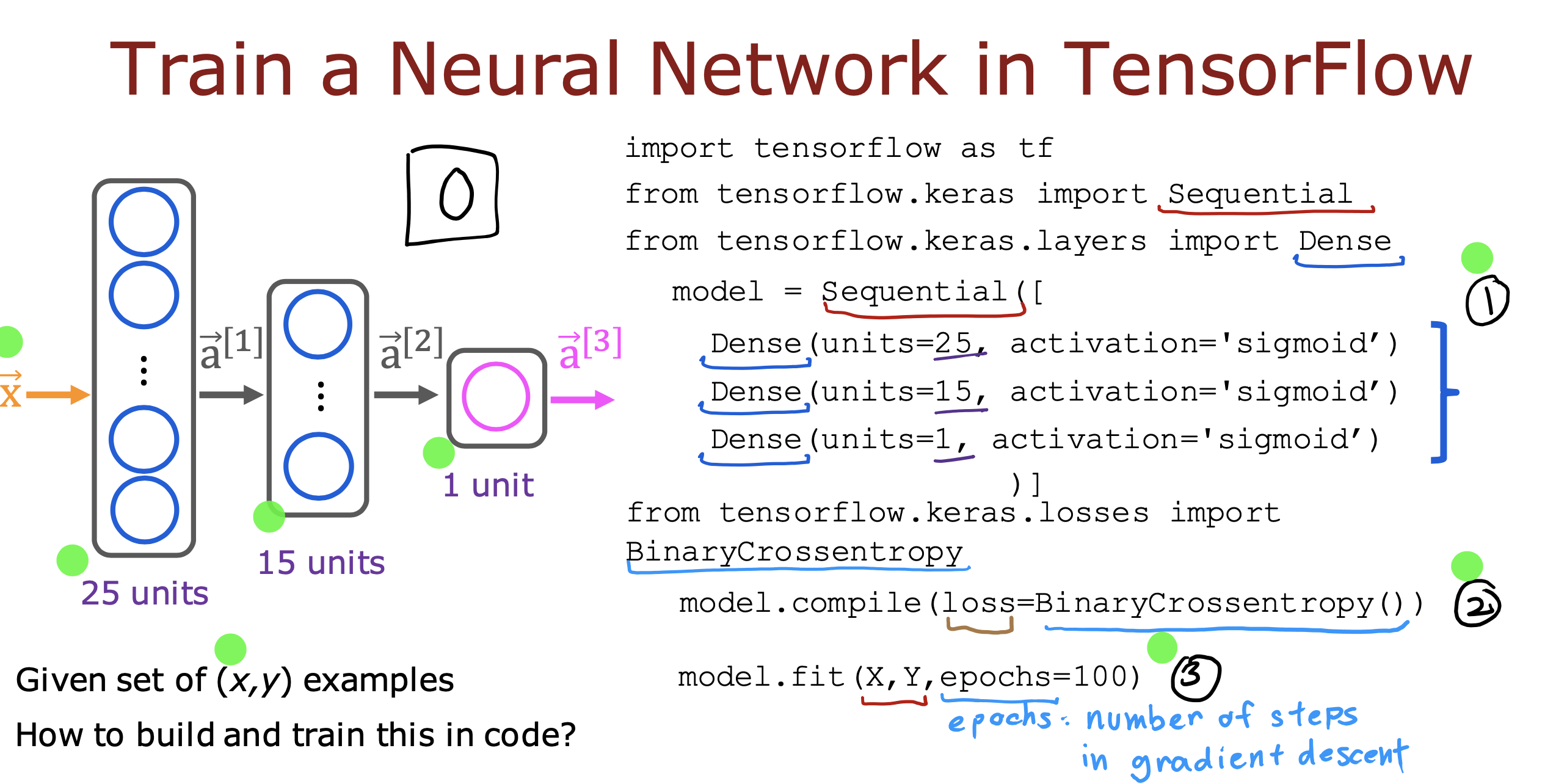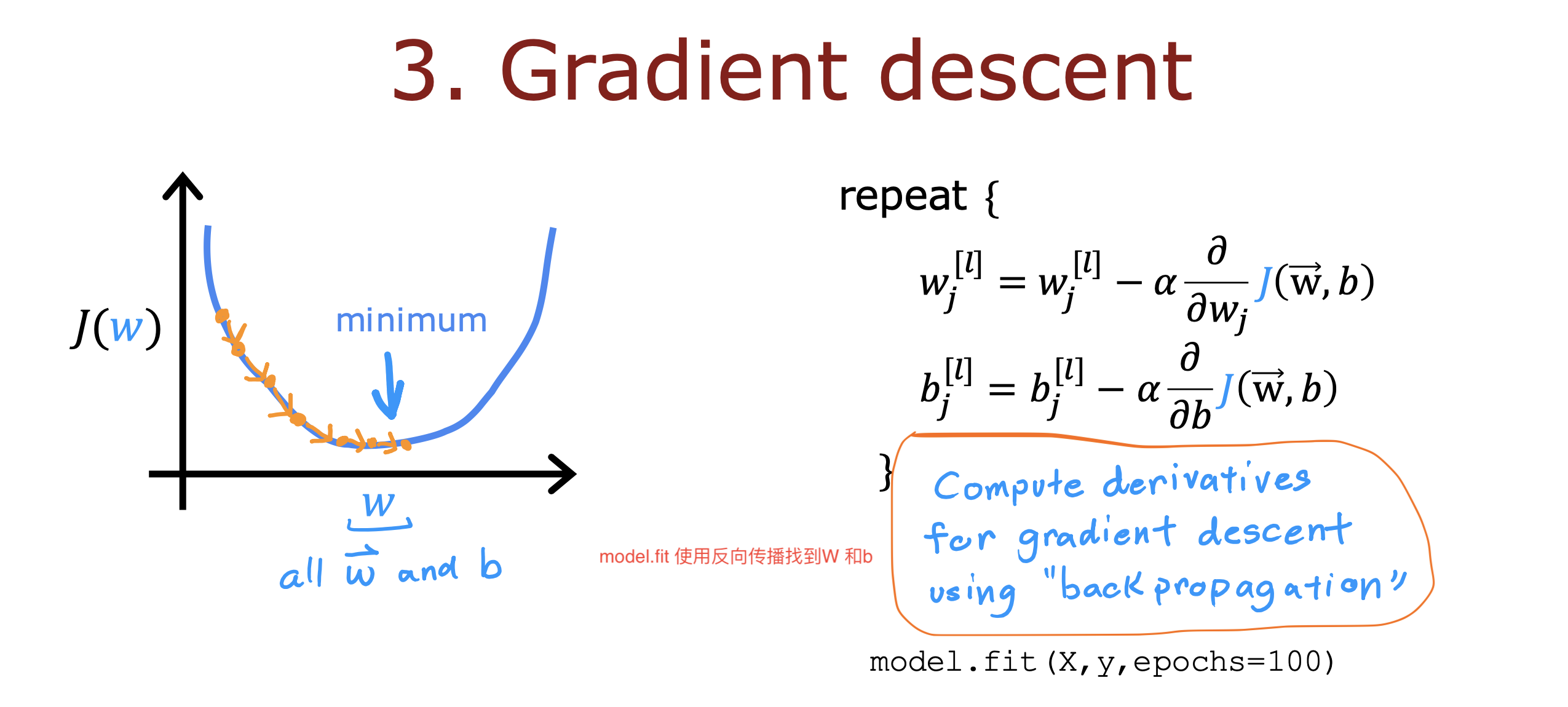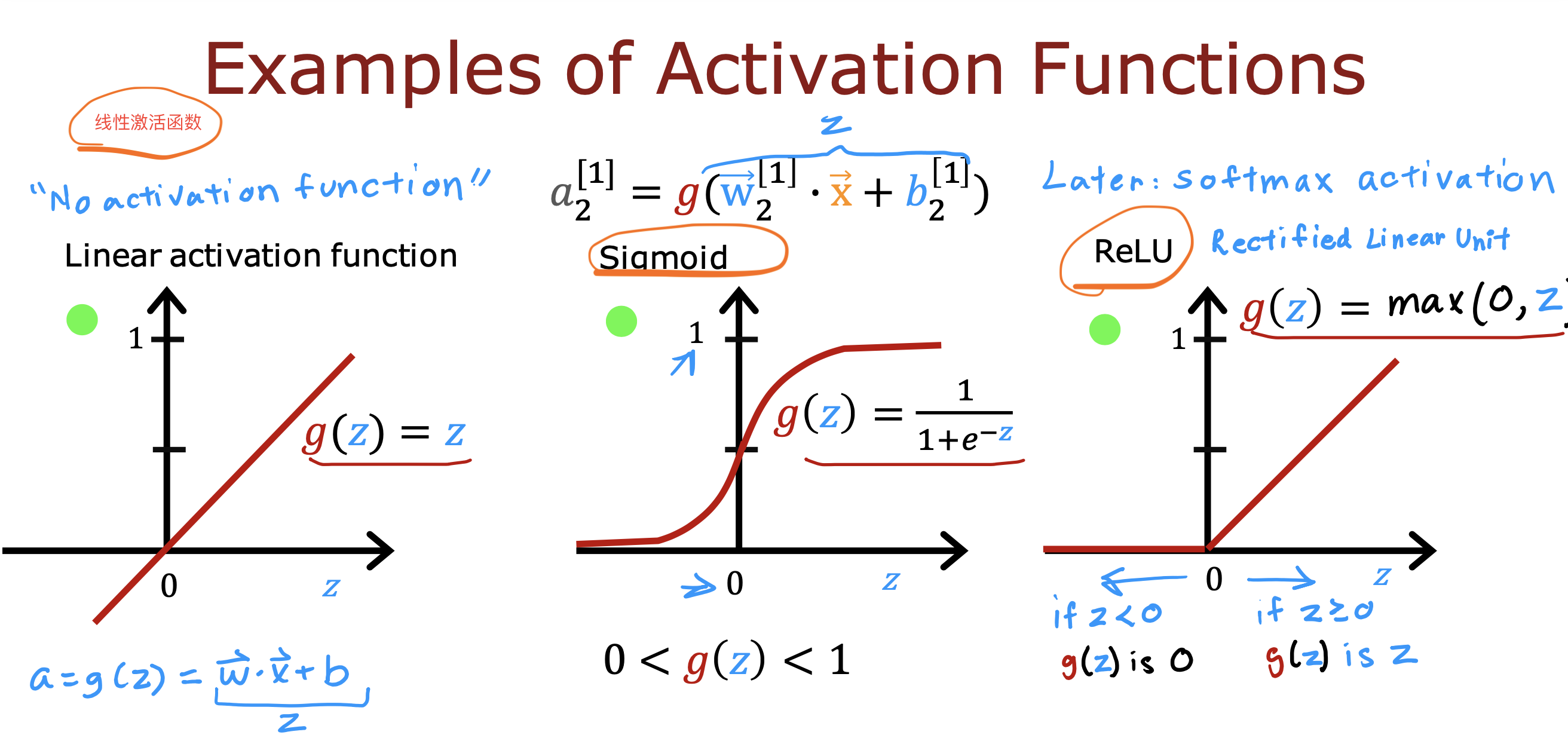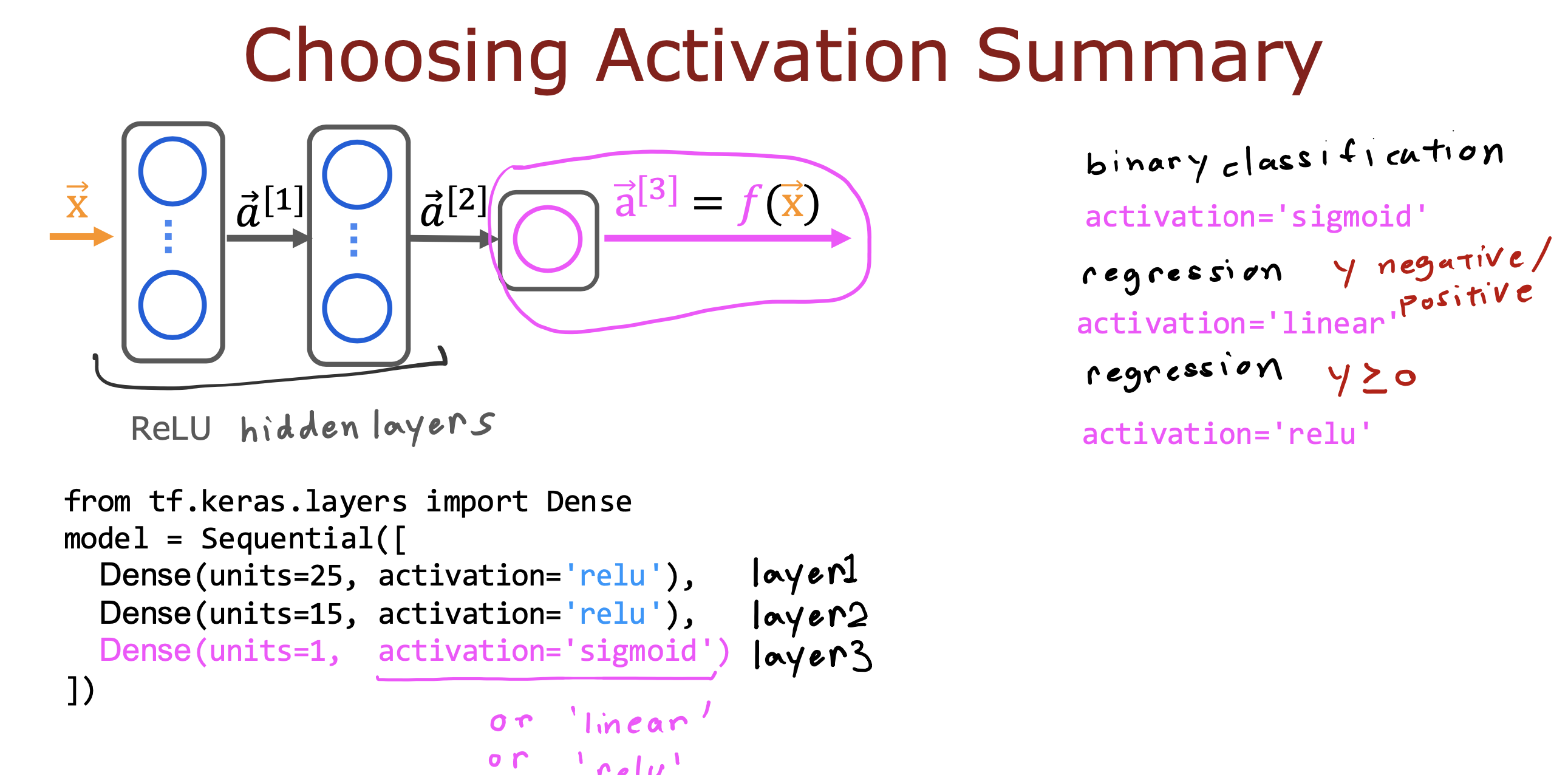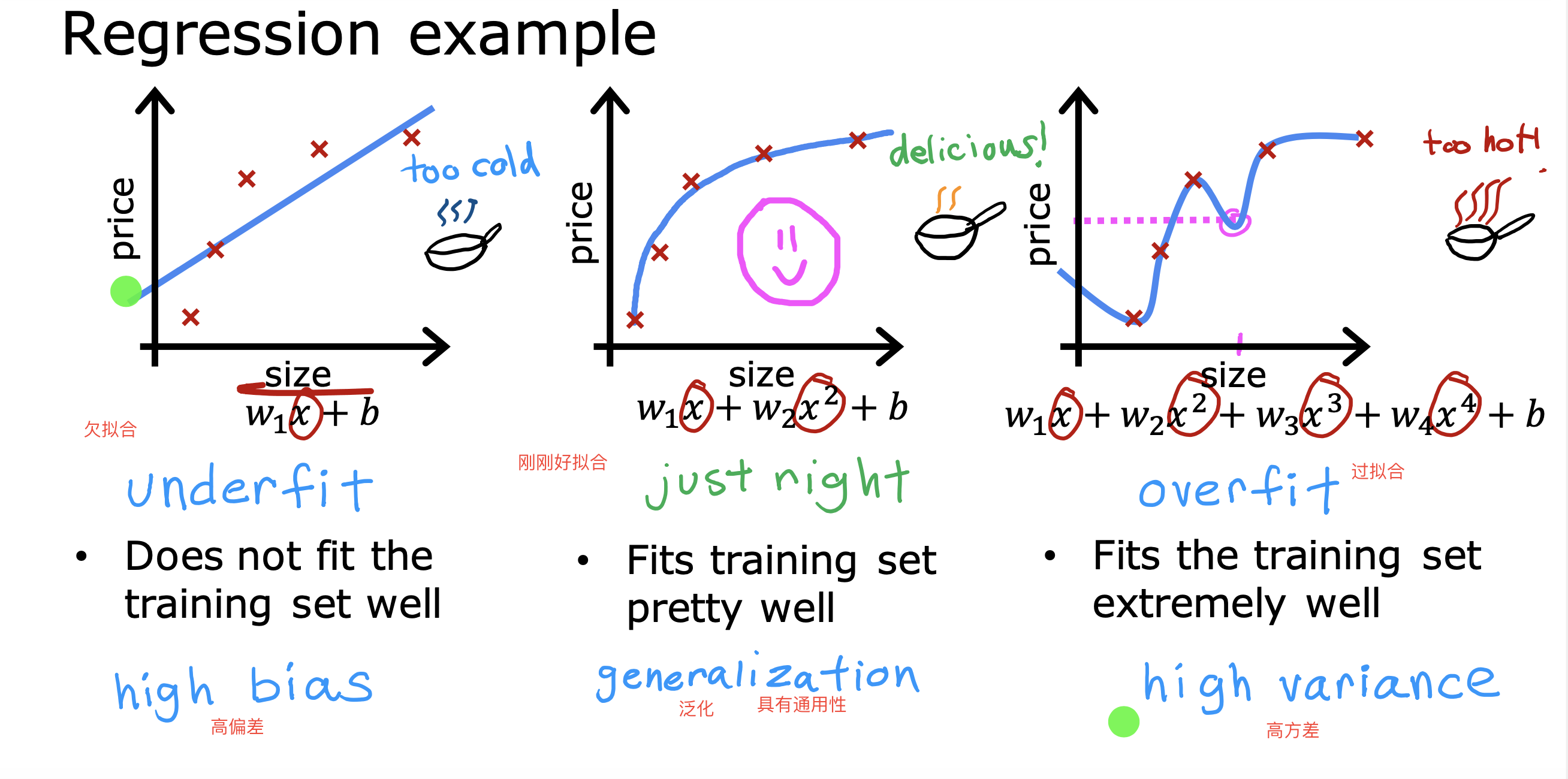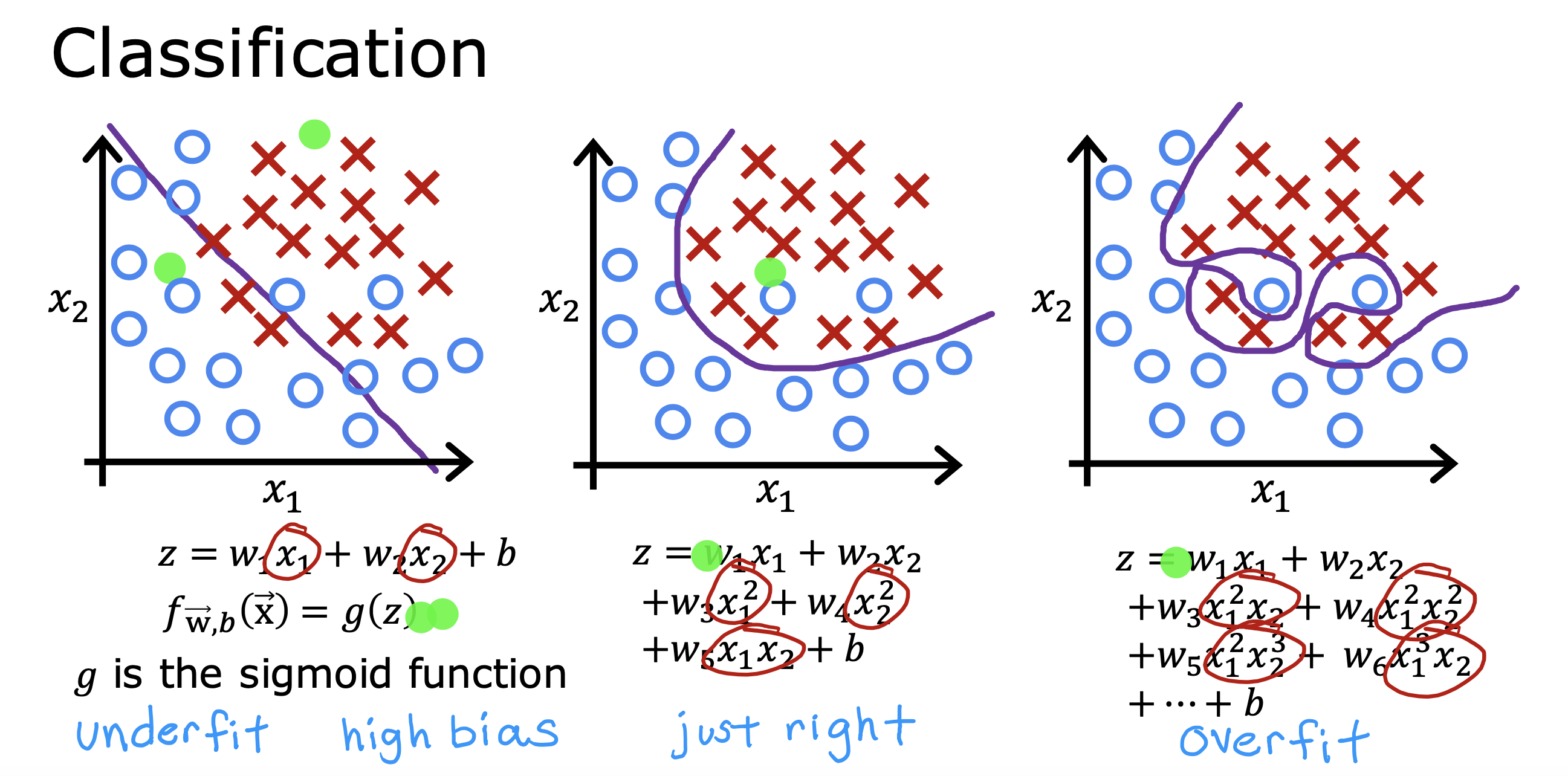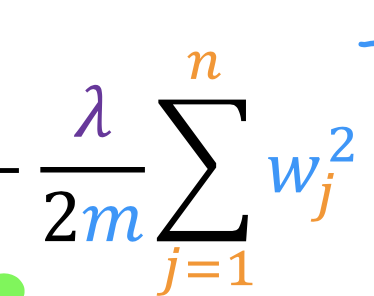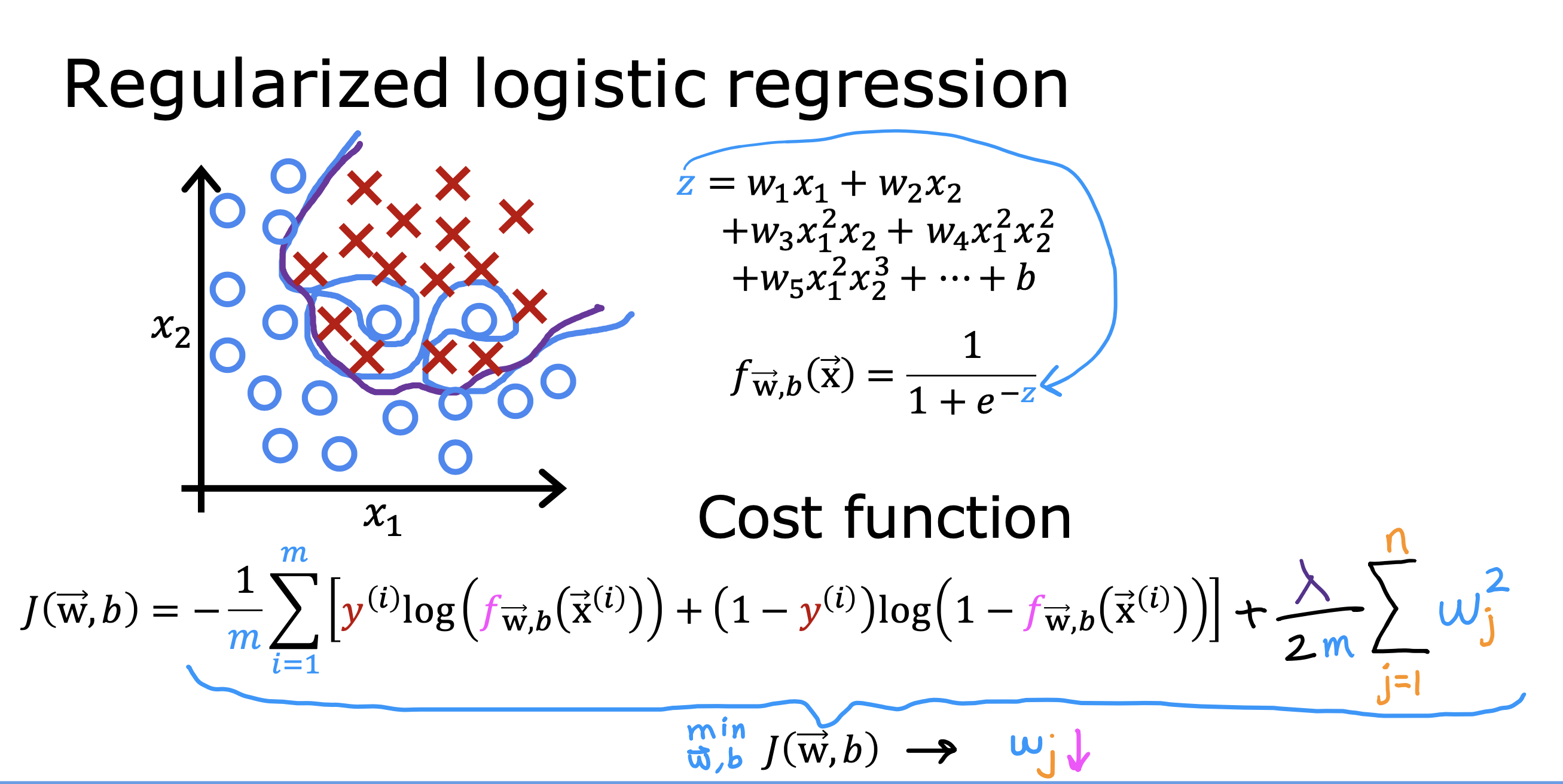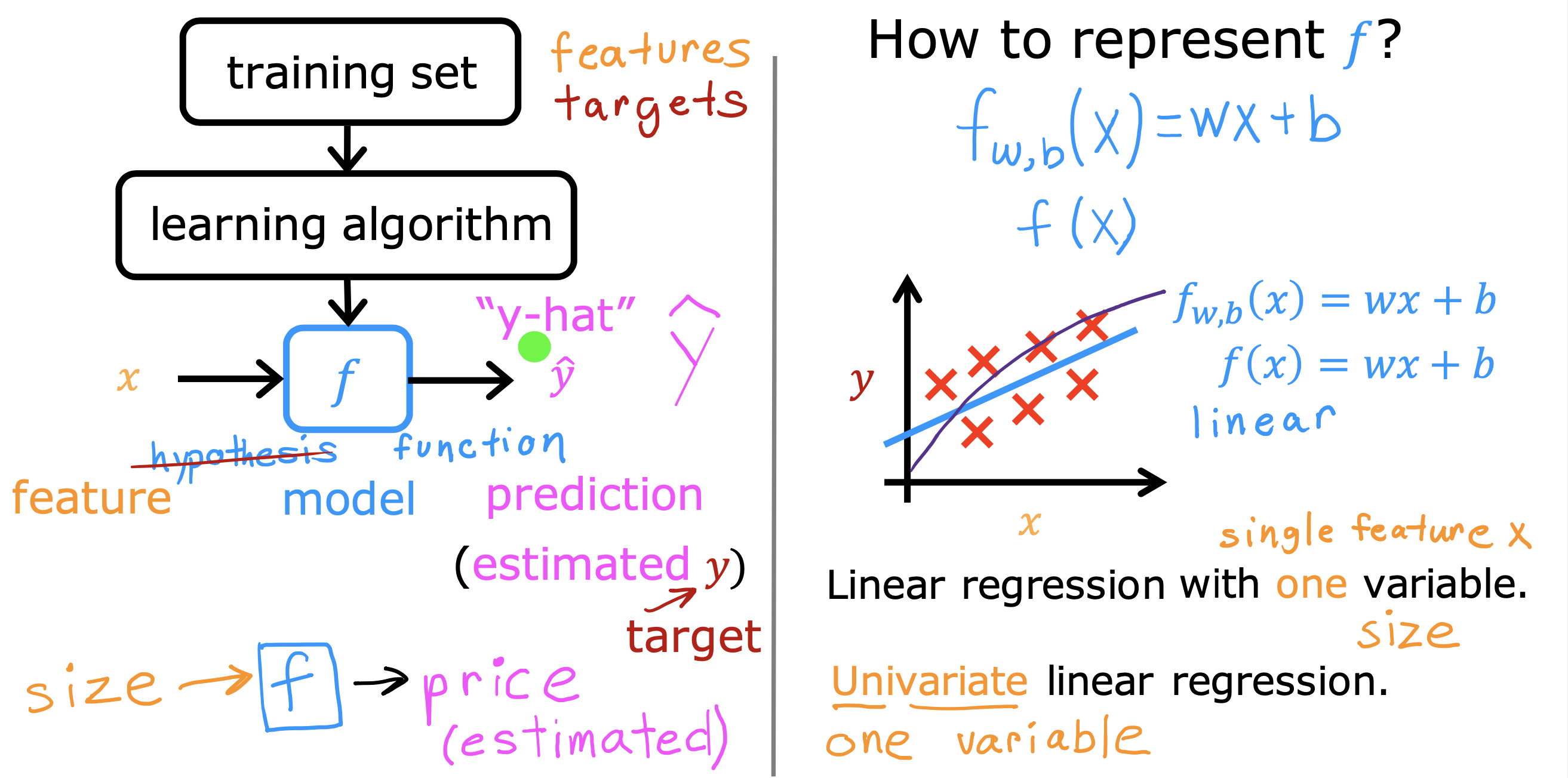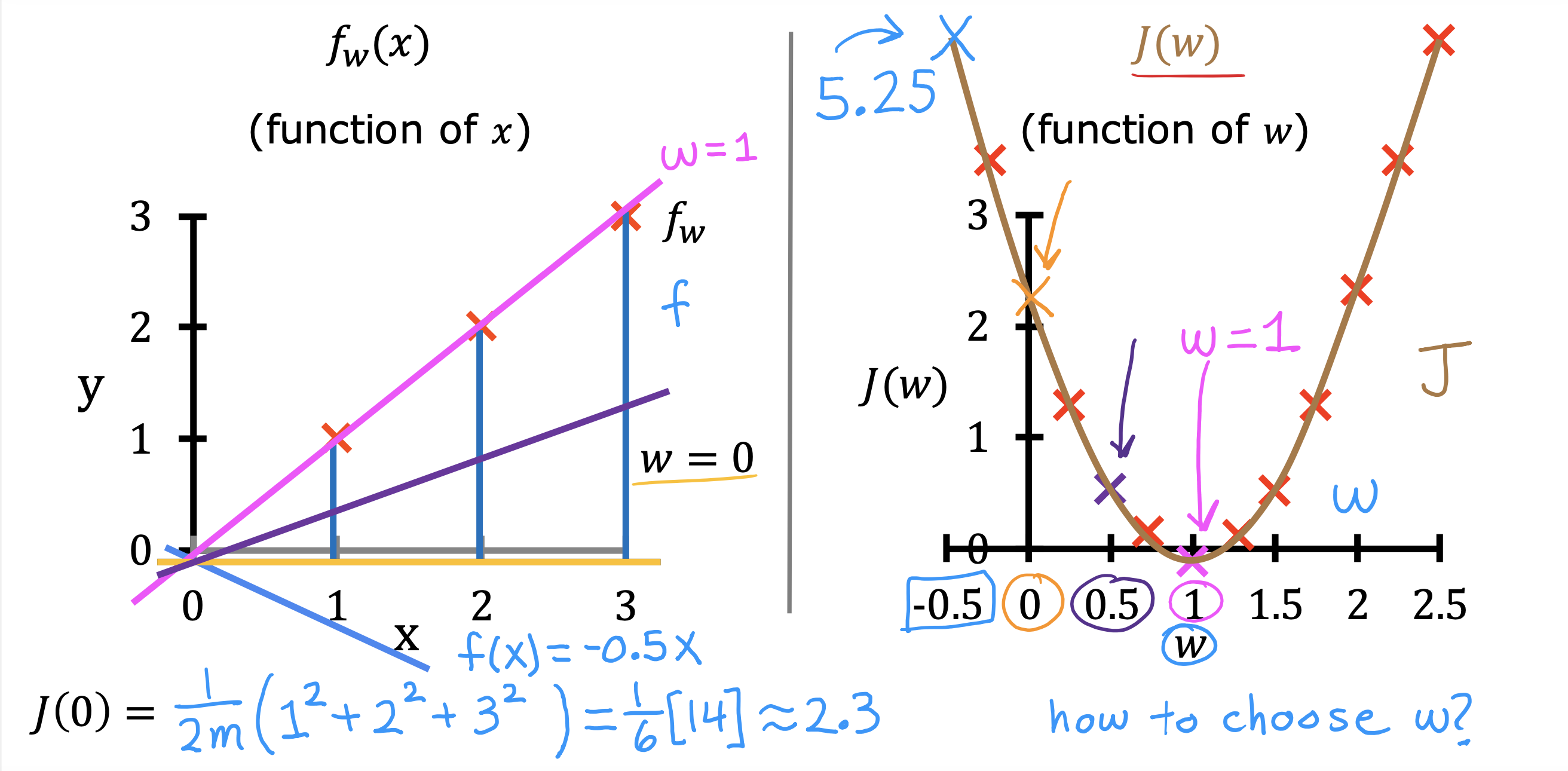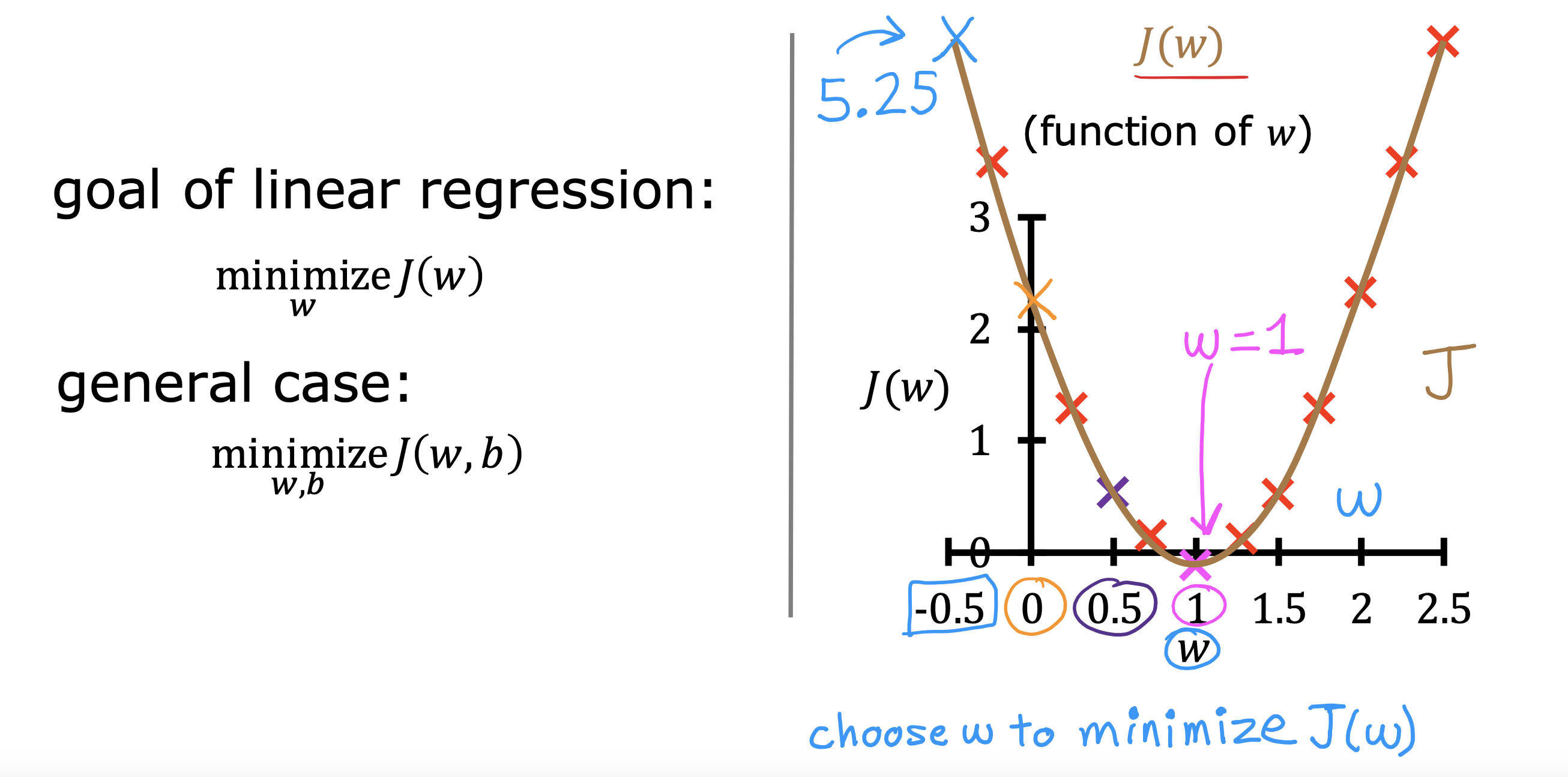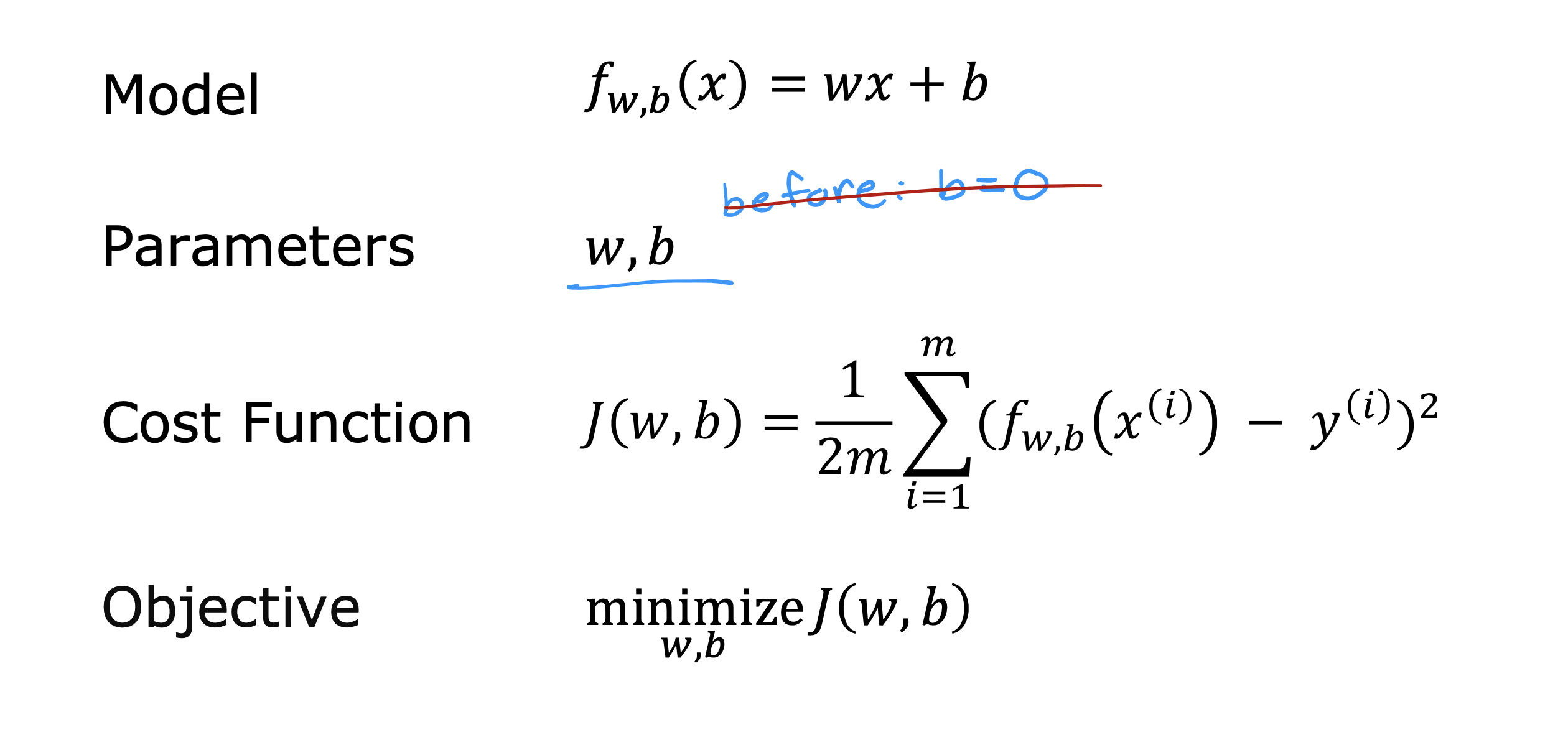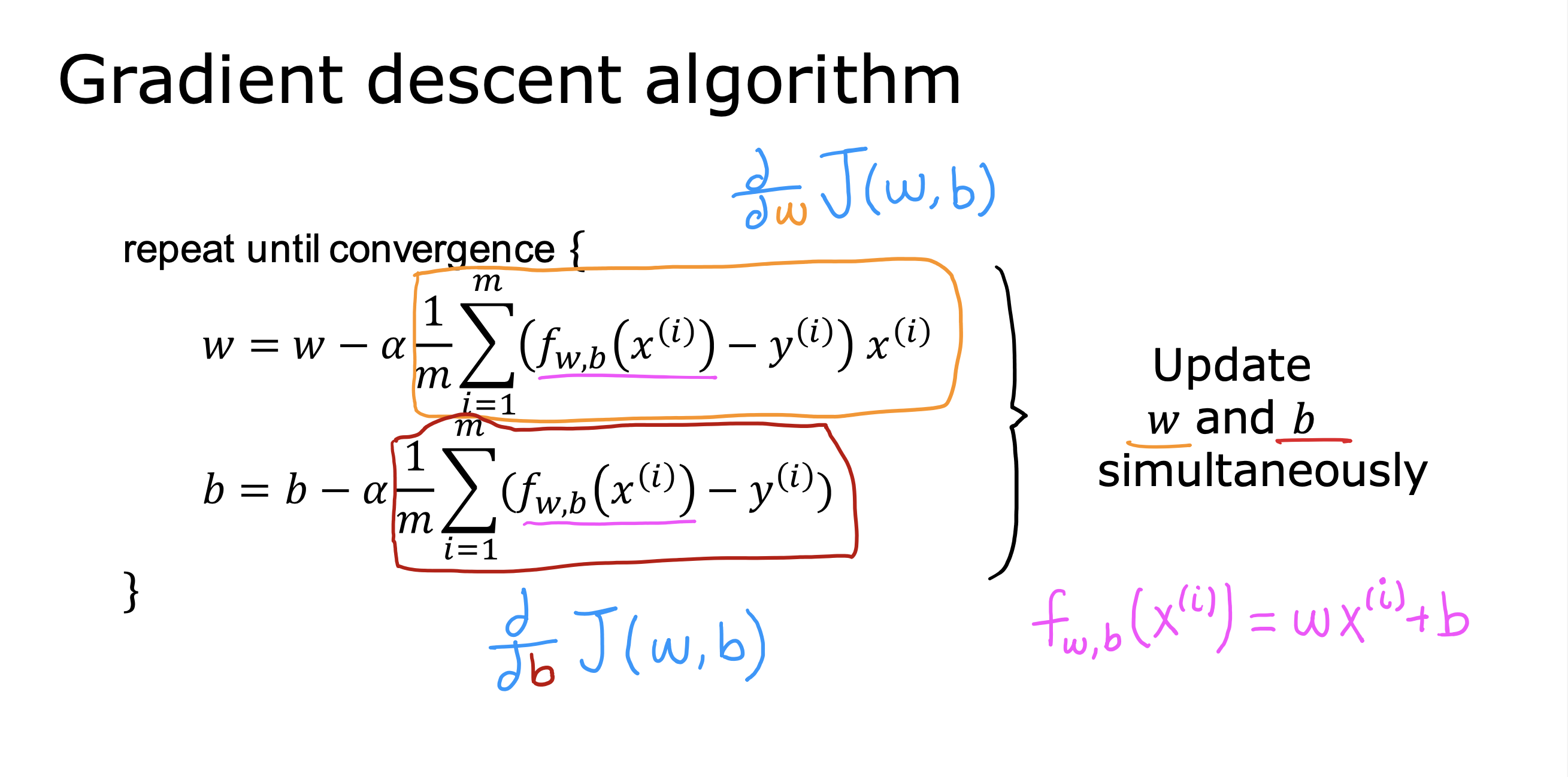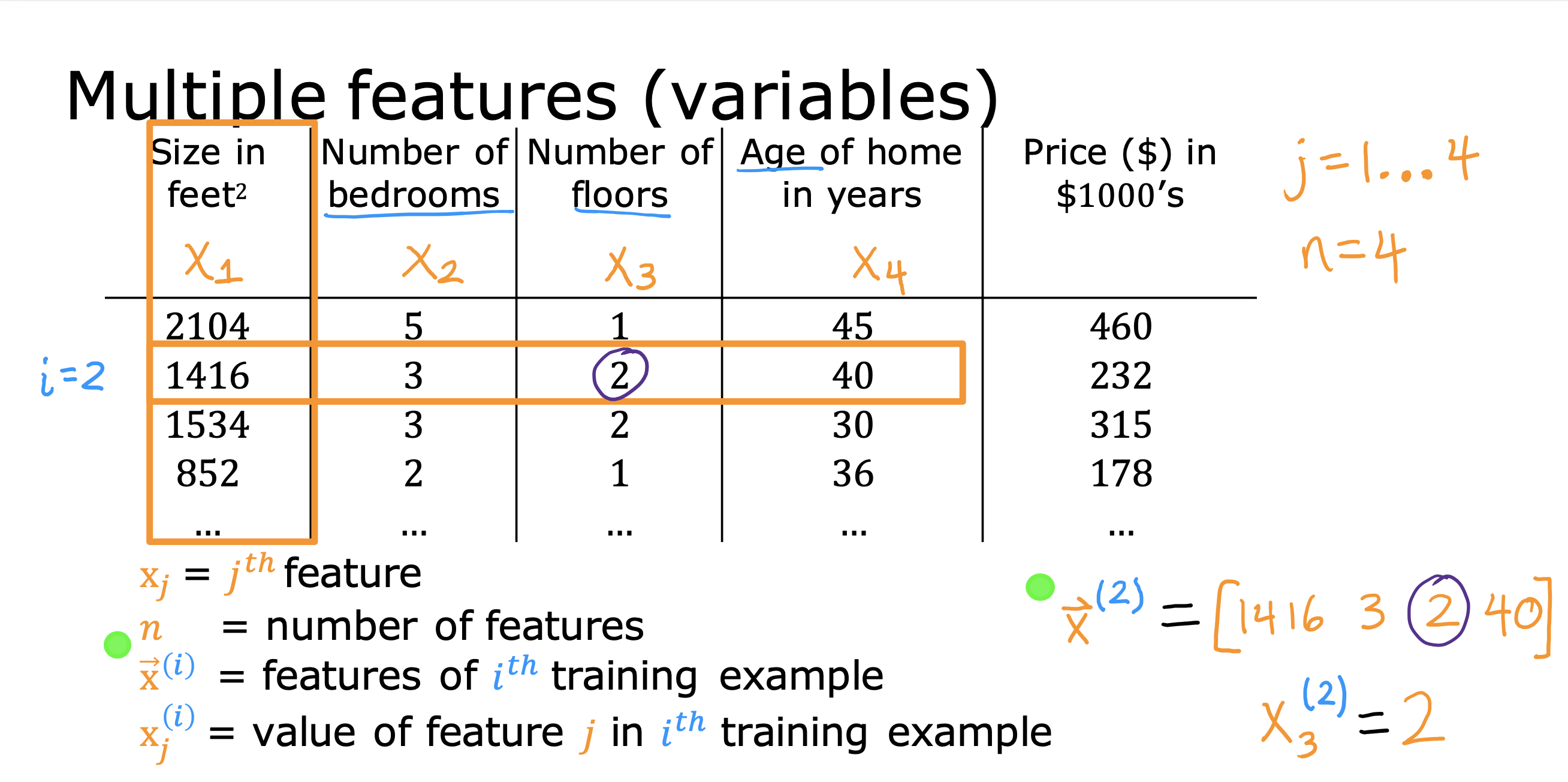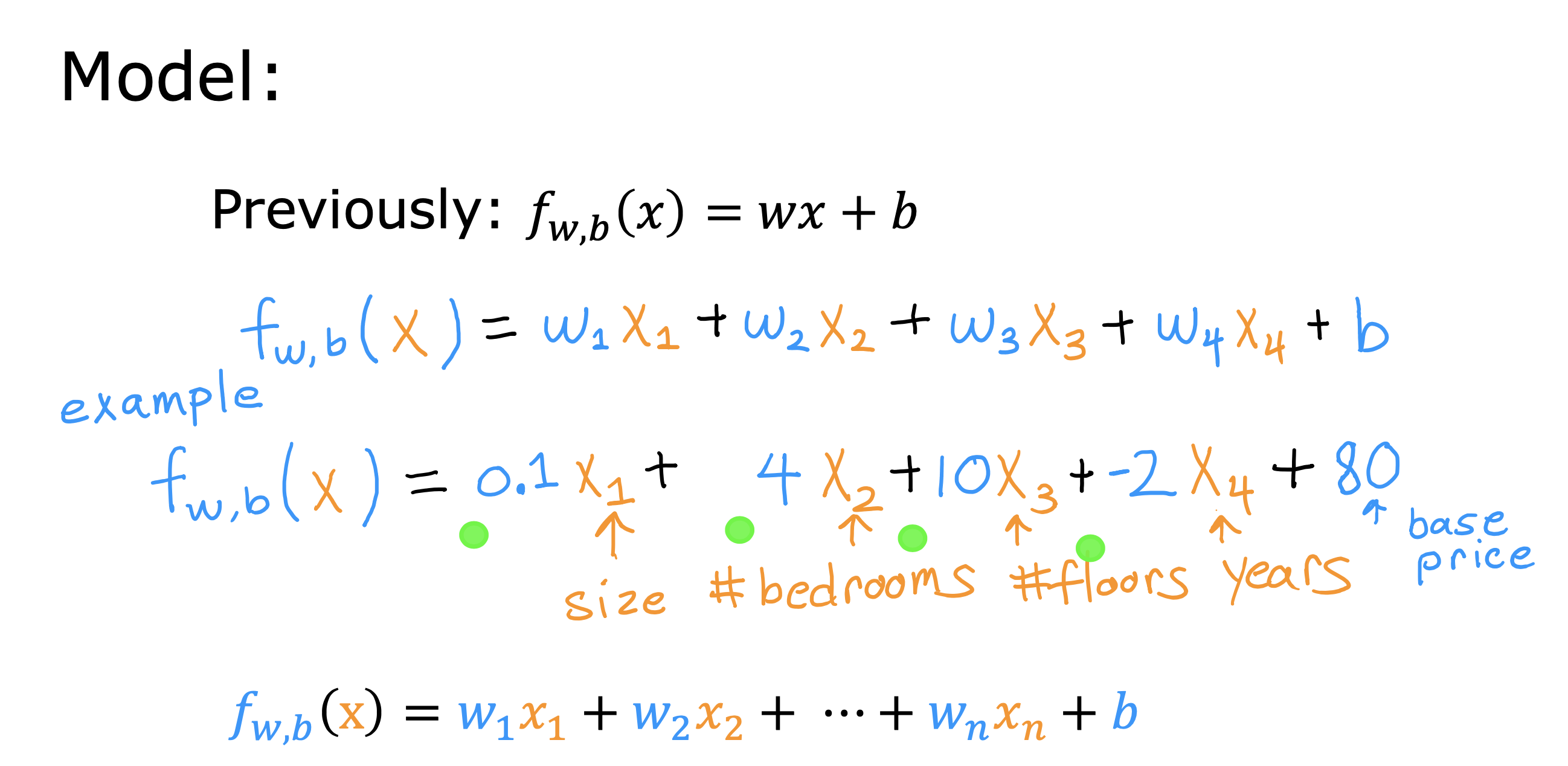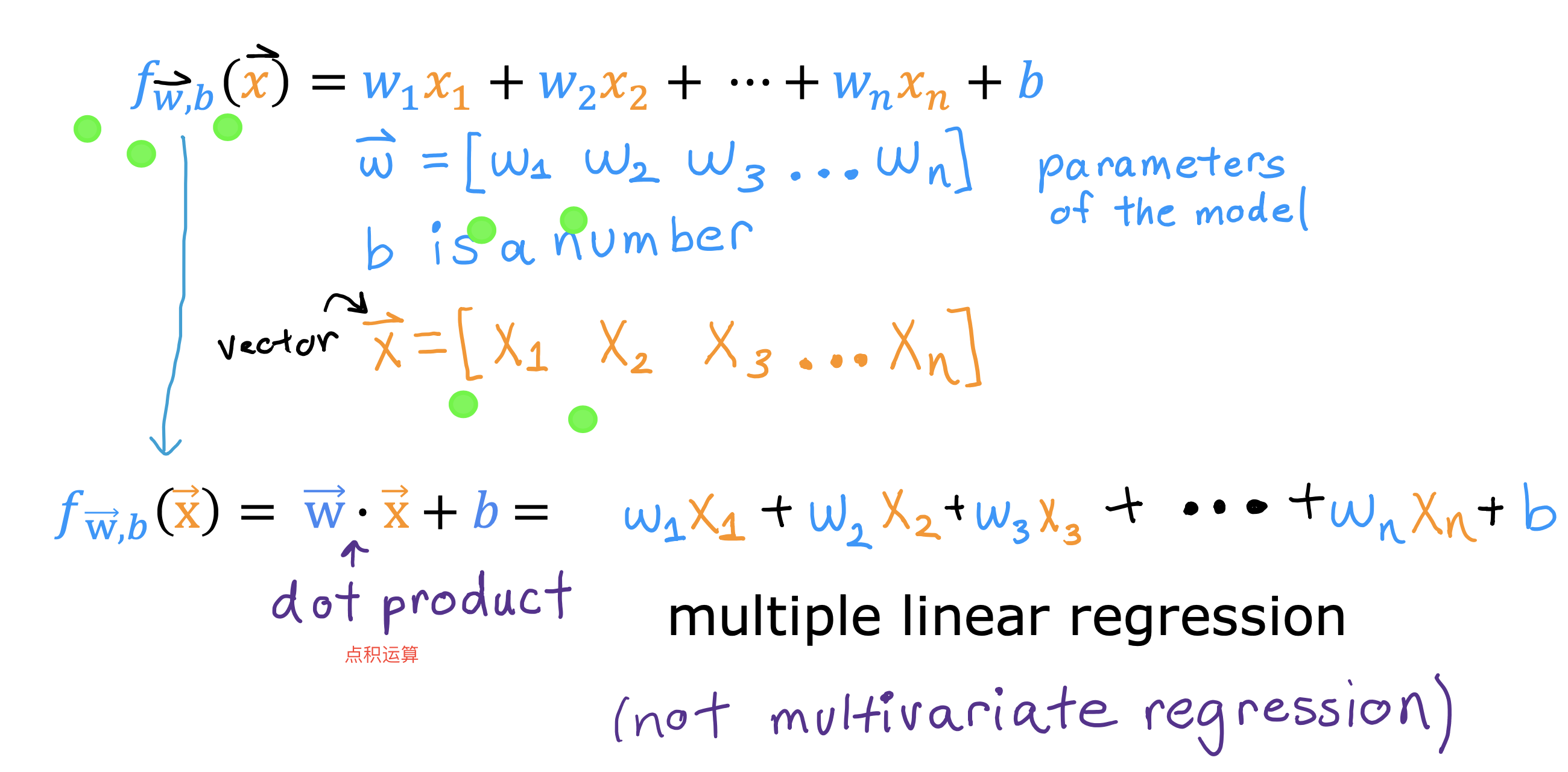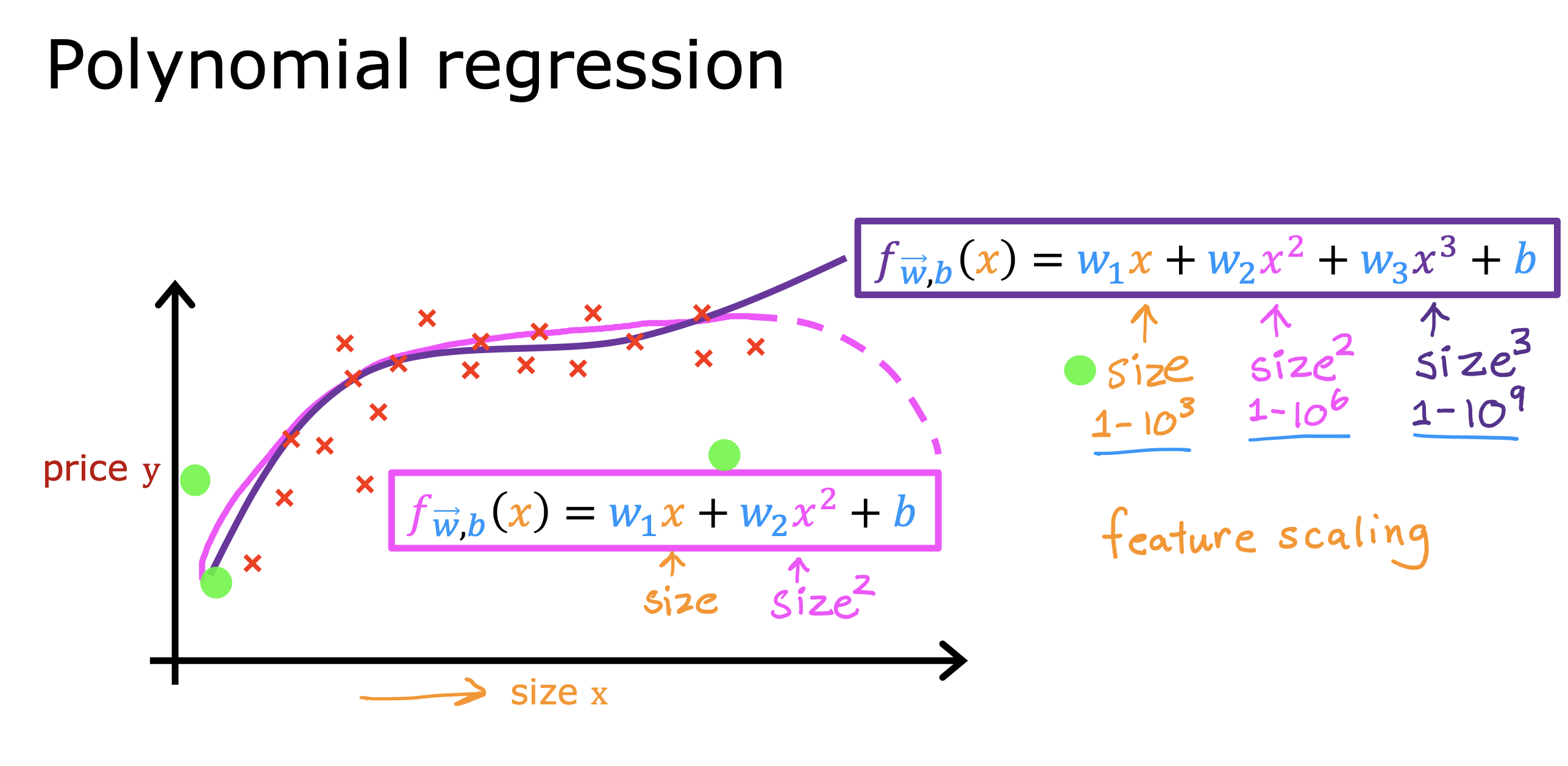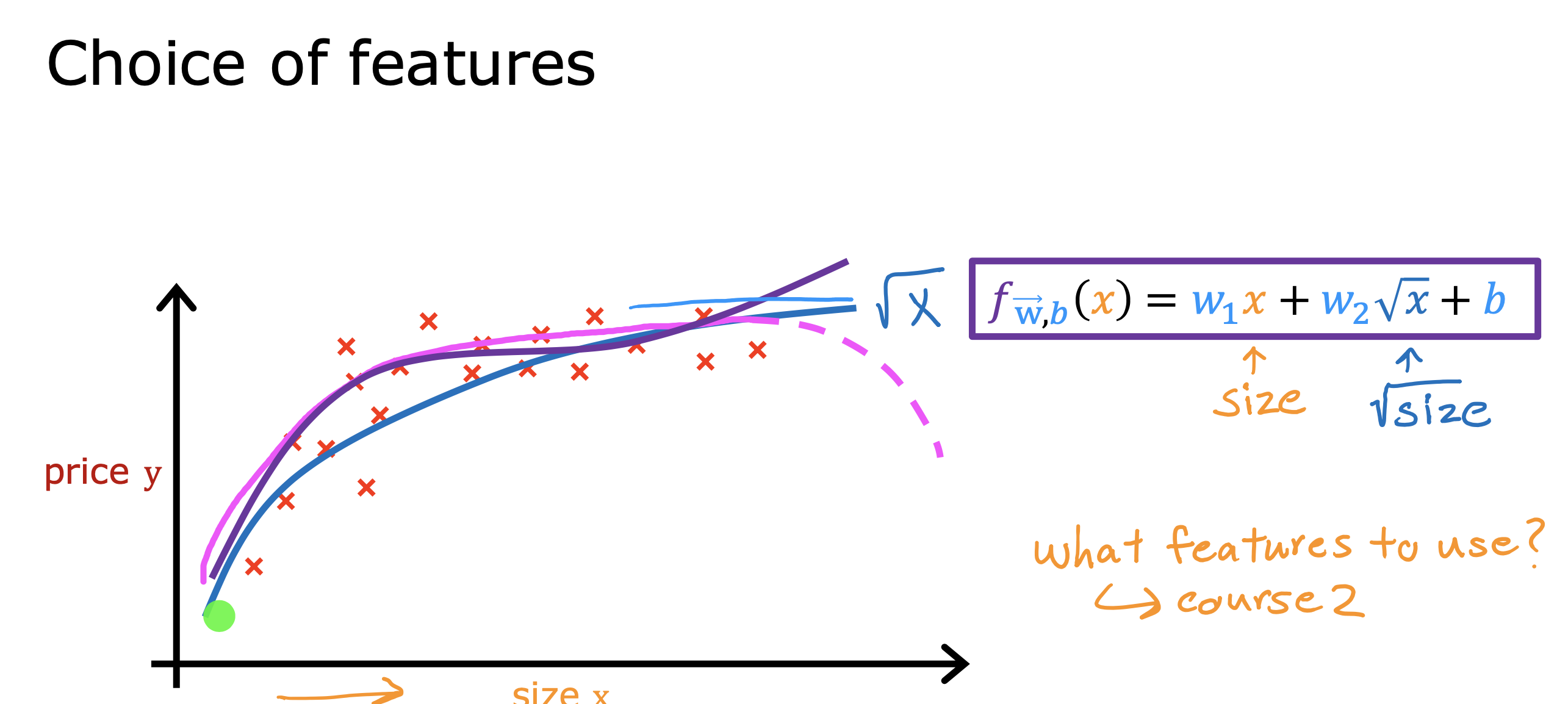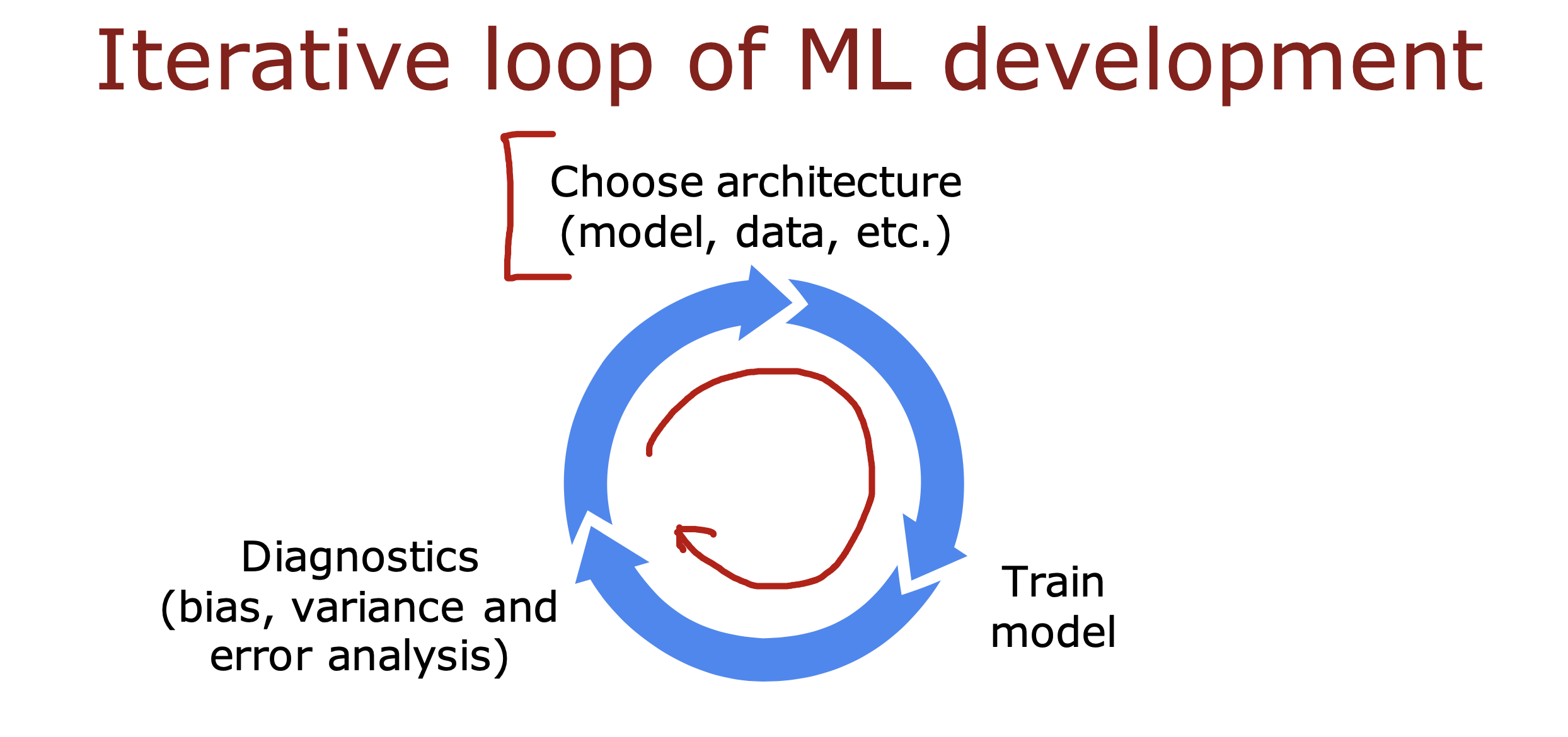
整个开发过程是一个选择框架，训练模型，诊断模型循环的过程

错误分析

除了从高偏差高误差角度对模型进行分析外，还可以对mcv 产生错误分类的角度对模型进行分析

可以从交叉验证集测试产生的错误中进行分析
通过将错误进行归类统计，找出对模型影响比例较大的错误和比例较小的错误
从而调整模型训练的方向，已解决上面遇到的问题

如果交叉验证集产生错误的数据比较庞大，可以选择进行随机抽取一定小批量的数据进行错误分类，以节省人力

添加数据

通过引入更多数据完善模型的判断，更关注通过注入的数据引发的对模型的训练结果的影响

数据增强

Augmentation: modifying an existing training example to create a new training example.
在原有数据基础上，通过添加特定种类的噪声，形成新的测试数据，从而完善特定种类的错误判断
对于图片和音频数据都适用

但是对添加随机或者无意义噪声产生的数据进行训练，对于模型训练不会有多大帮助

数据合成

Synthesis: using artificial data inputs to create a new training example.
直接由计算机合成训练过程中使用的数据，通常用于计算机视觉训练的场景

迁移学习

在已有大模型训练结果基础上，通过修改输出层结果使之符合自己使用场景的训练方法
好处是，在数据有限的情况下，可以直接使用输出层之前的参数开始训练，减少自己从头开始训练的工作

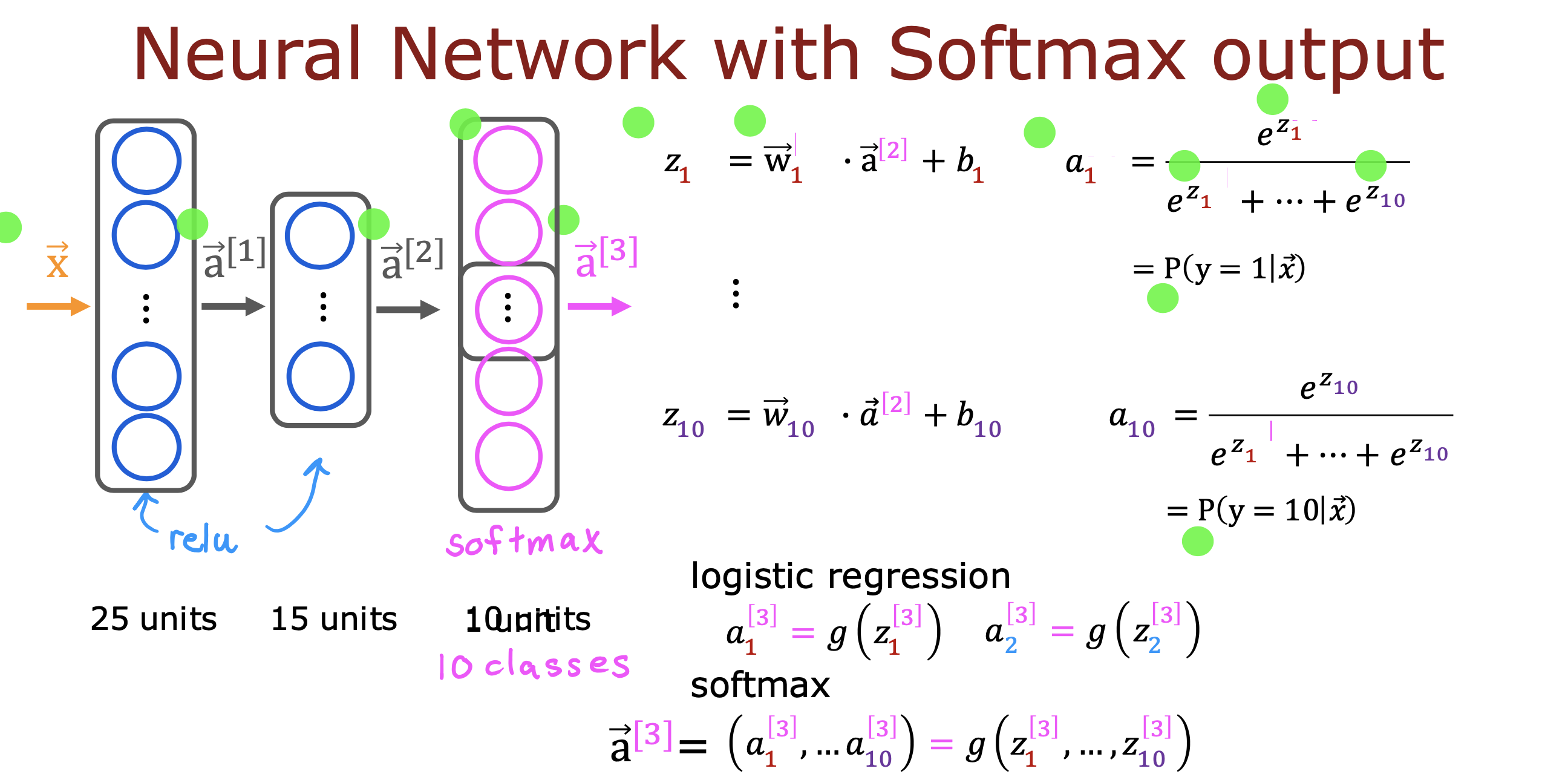
例如下面这个使用1000+分类的训练识别数字0-9的模型，只是在输出层将1000+ 输出改成10种输出，在此基础上开始训练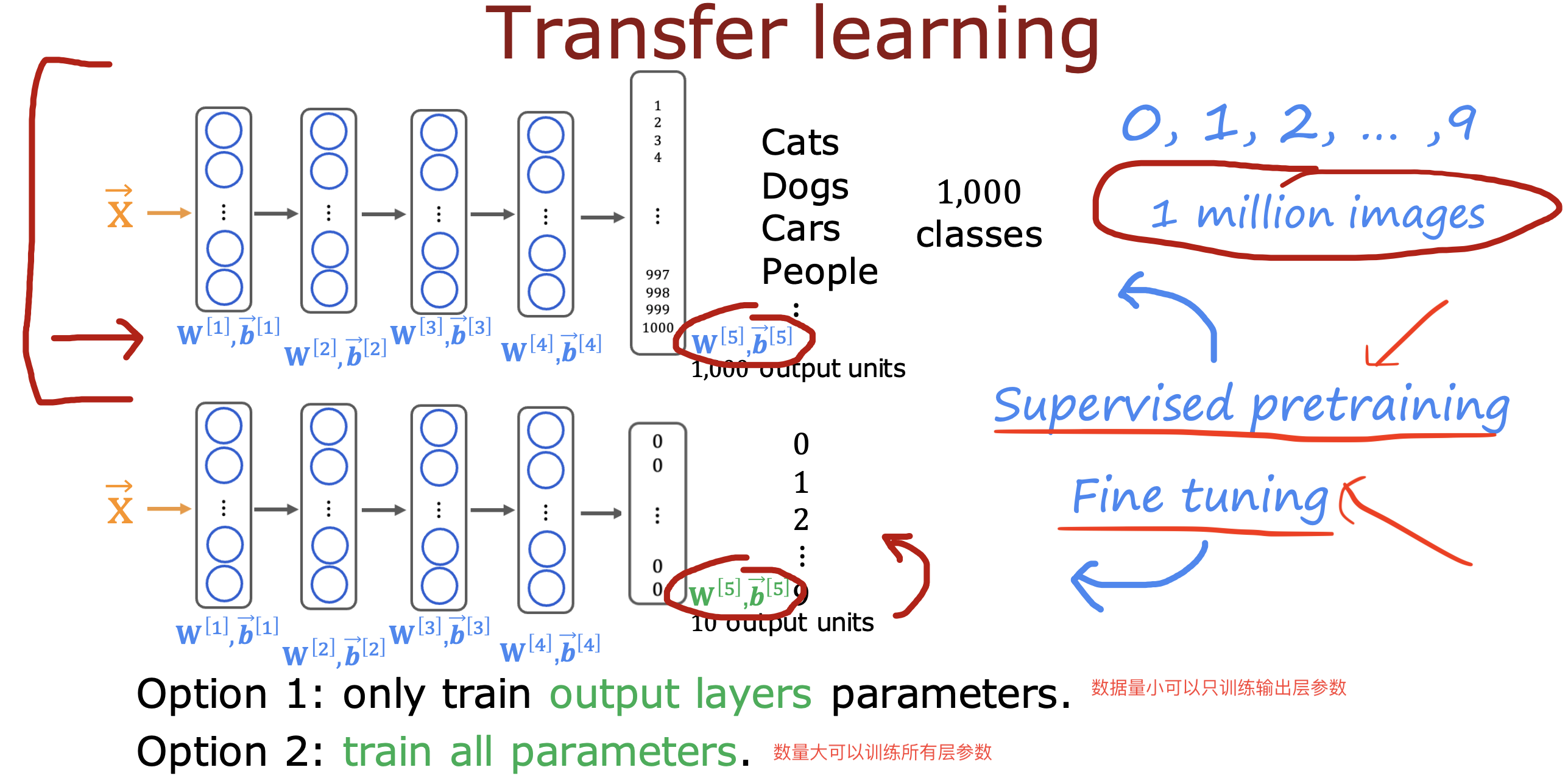

一般训练步骤为下载相同输入(文本的下载文本的，音视频的下载音视频的)的预训练模型，然后用自己的数据进行训练(fine tuning)

完整开发流程

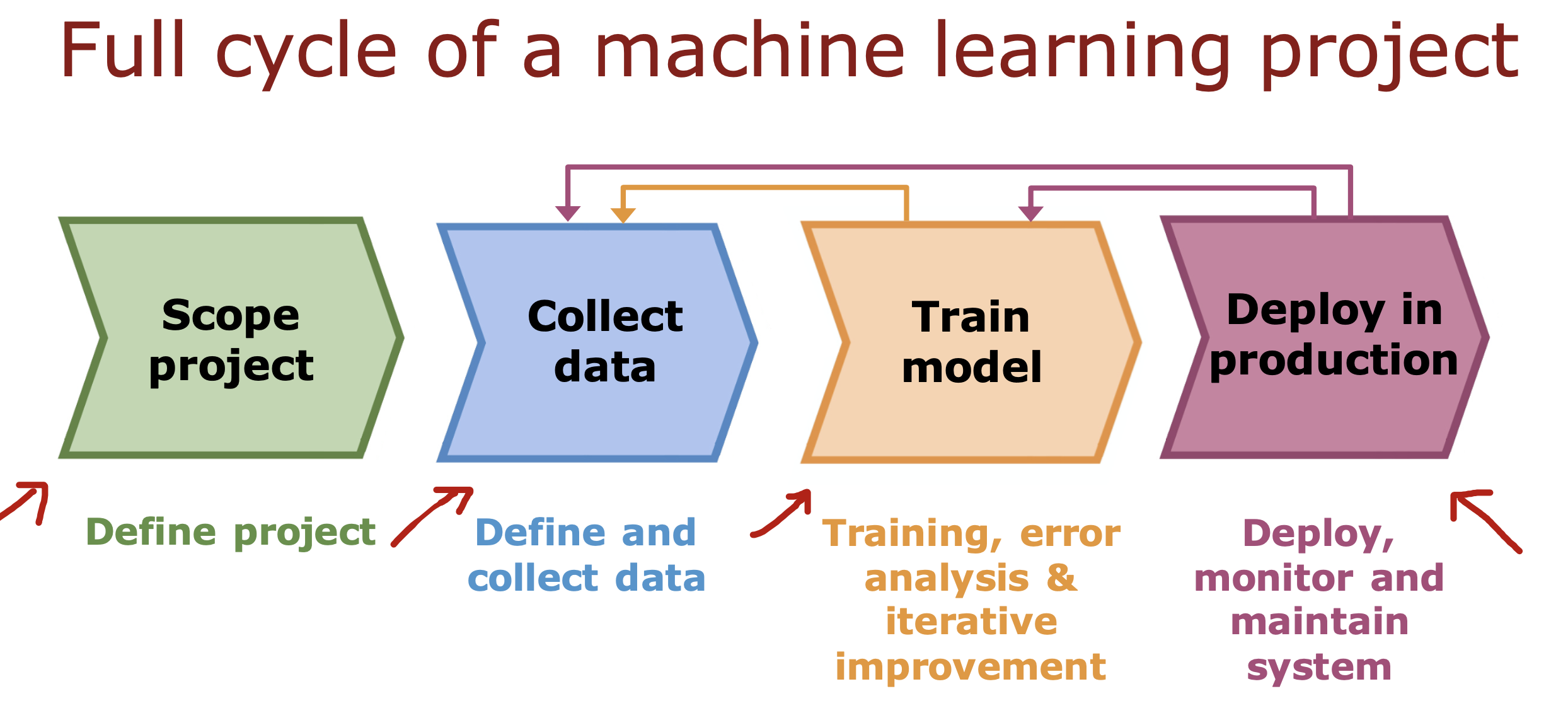
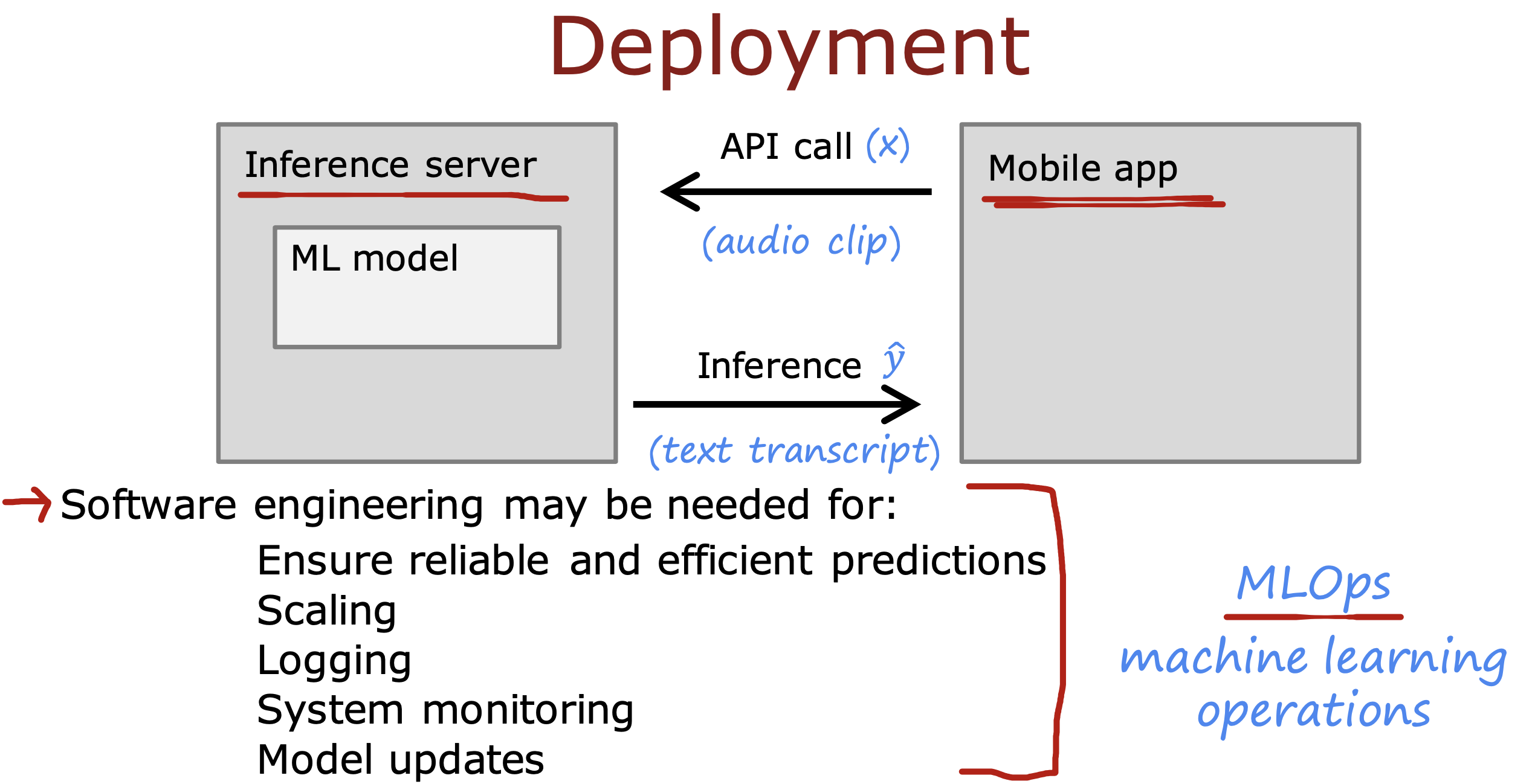
部署阶段

通常应用层跟模型通过Api 进行通信，用户输入x， 模型返回预测值y^
软件工程师需要注意

1. 尽可能的保障低成本的计算出具有可靠性和有效性的预测结果
2. 可以进行大规模用户扩展使用
3. 在用户隐私允许同意的情况下进行日志记录输入和输出
4. 对模型进行系统监控，比如根据上面日志的记录，计算出因为当前数据变化导致计算结果不准时，判断是否让模型进行进一步优化
5. 保障模型更新，在上一步进行模型优化后要保证能够将老的模型替换成新模型

避免道德偏见伦理问题

1. 建议多元化(多背景，多种族)团队，上线前进行头脑风暴，探索可能对弱势群体造成伤害的可能
2. 参考行业标准
3. 上线前通过技术诊断产生的伤害可能性，从而决策是否可以上线
4. 制定延缓计划，上线后观测可能产生的伤害，及时进行回滚处理
   

二分类错误度量

在对倾斜数据集(y=1 和y = 0 所占比例不是5:5)进行训练时，
判断模型预测结果好坏通常交叉验证集的数据计算精确率和召回率两个指标衡量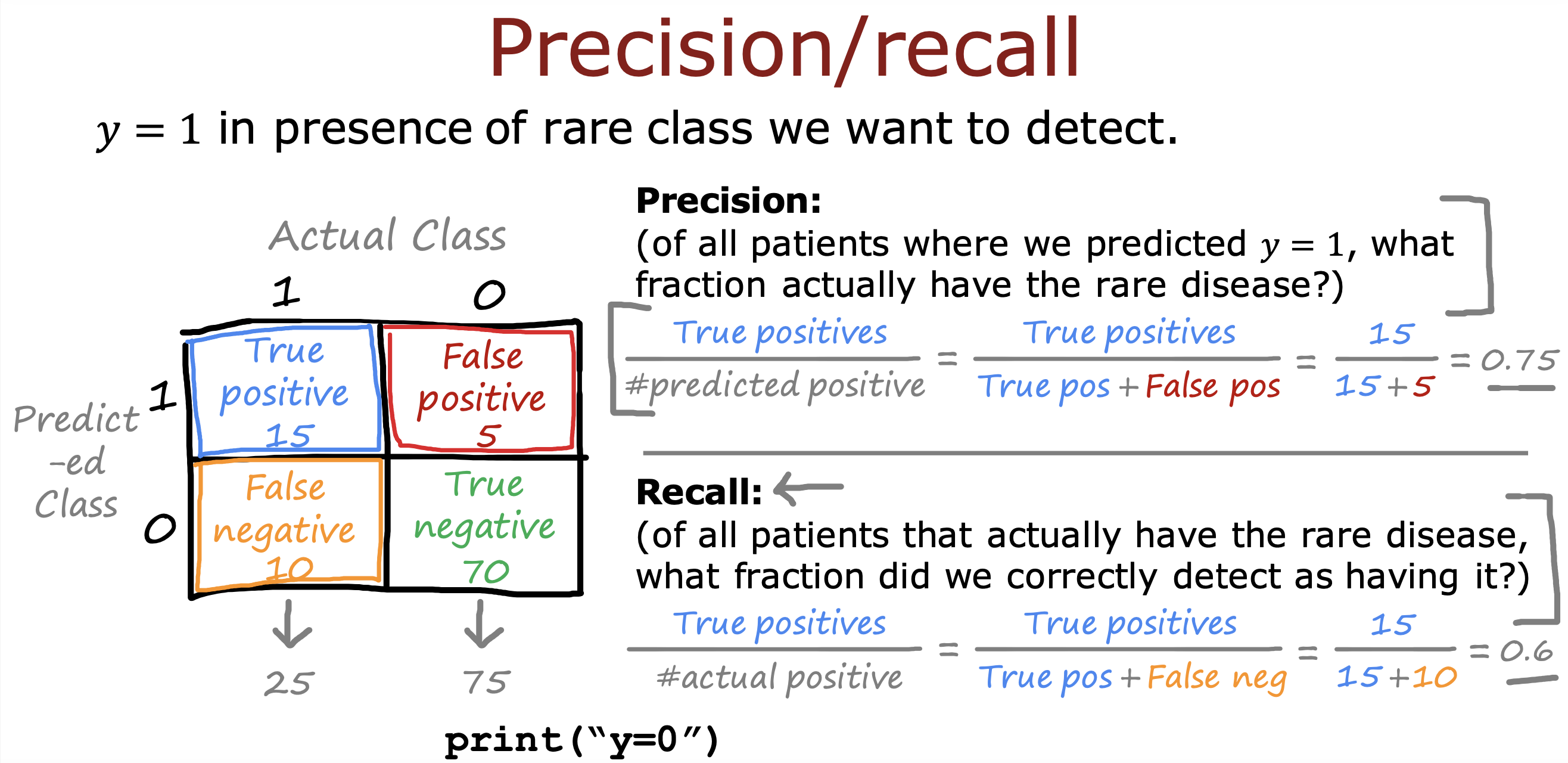

如果二者都趋近0或1时，说明当前的模型不是一个有用的模型，一直在打印0或1
只有二者值都很大时，才说明算法是有用的

精确率表示实际上y = 1的可能性
召回率表示模型计算出y = 1 的可能性

对于精确率和召回率的衡量

一种是通过设置阈值大小去权衡二者，从而进行取舍
提高阈值，会增加精度，降低召回率
降低阈值，会降低精度，提高召回率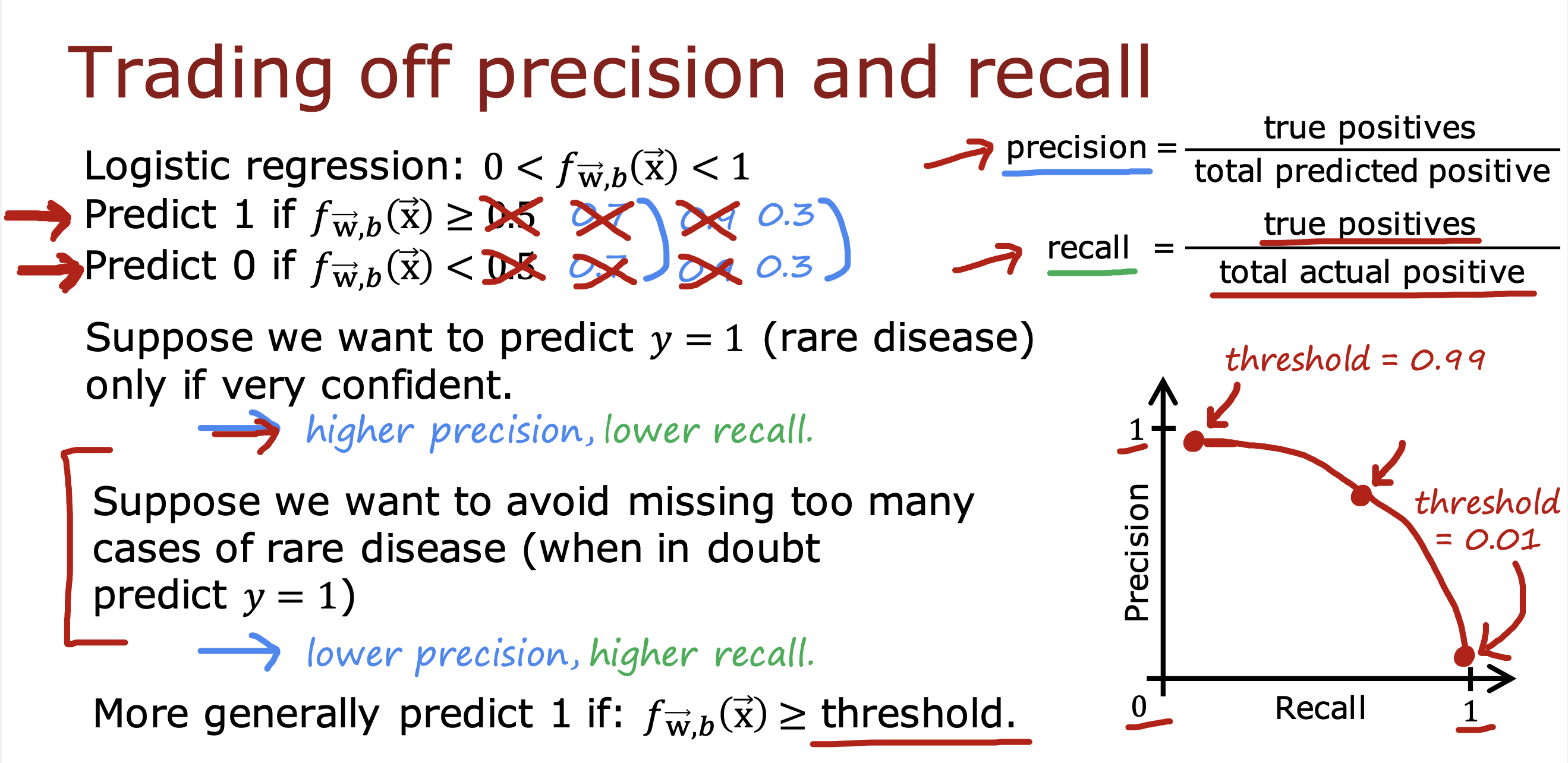

另外一种是使用F1 score分数(调和平均数)，自动计算出最佳的精度和召回率，从而选择对应的算法

通过判断高方差和高偏差的大小可以判断模型的性能问题
一般有以下两个性能问题
高偏差意味着模型欠拟合
高方差意味着模型过拟合

高偏差的情况下，
Jtrain 值会比较大，且Jtrain和Jcv 值相近
也就是说Jtrain 较高对应的训练数据的拟合度本身就不够

高方差的情况下，
Jcv 会远大于Jtrain, Jtrain 值可能比较小
就是说模型对训练数据很拟合，但是对交叉验证数据不够拟合

也有高方差和高偏差两个问题同时存在的情况
Jtrain 值会比较大，且Jcv 远大于Jtrain,
这种情况意味着模型可能对一些数据过拟合，对一些数据又存在欠拟合

正则化参数𝜆 对模型的影响

如果𝜆偏大会导致Jtrain 偏大，出现欠拟合
(想象𝜆现在是一个非常大的数值，为使Jtrain 最小，就会让w值逐渐趋近0, 最终模型无限接近b)
如果𝜆偏小会导致Jtrain 偏小，但是Jcv 偏大，出现过拟合
(想象𝜆现在无限趋近于0，或者直接等于0， 那么要使Jtrain 最小，w取值就得变大，多项式就会被保留，最终模型出现过拟合)
如果𝜆取值适中就可以实现Jtrain和Jcv 值都偏低，模型适当拟合的效果

𝜆 如何取值

通过选取不同 𝜆 带入计算最小损失函数，用得到的(w,b)值计算Jcv, 选取多组Jcv 中 最小值的(w,b)进行Jtest 计算，

𝜆 趋势图

𝜆 对于误差的影响趋势和多项式对误差的影响趋势呈镜像关系
𝜆 值从小到大，Jtrain 从小到大，模型从过拟合到欠拟合
多项式平方数从小到大，Jtrain 从大到小， 模型从欠拟合到过拟合

建立性能基准线来判断模型性能

计算基准线与Jtrain 的差A， A 如果偏大说明模型存在高偏差欠拟合问题
计算Jtrain 与 Jcv 的差B，B 如果偏大说明存在高方差过拟合问题
如果A 大于B 说明存在高偏差，欠拟合
如果A 小于B 说明存在高方差，过拟合
如果A 和 B 数值接近，说明 高偏差和高方差同时存在

基准线可以来自
人类的测试水平
竞争算法的性能水平
基于过程经验判断的水平

以 语音识别为例

学习曲线

Jtrain 和Jcv 随 训练集大小m变化的趋势曲线被称为学习曲线

一般情况下，
Jtrain 会随m 变大逐渐变大，因为为了拟合更多数据，数据比一定会散落在曲线上，误差累加起来数值会变大
Jcv 会随m 变大逐渐变小，因为更多的数据可以展示更多的情况，是模型拟合度更高，对于Jcv 计算就是越小

但是对于存在高偏差的模型，增加样本数量并不一定能对模型拟合产生多大帮助，
因为高偏差模型具备欠拟合特点，随样本数增加损失函数也会增加，且相对基本线误差依然存在

对于存在高方差的模型，增加样本数量可以起到一定帮助
因为高方差模型具体过拟合特点，会将增加的样本继续拟合到自己的训练模型中，相当容纳近了更多的数据情况
可以更好的拟合实际的情况

小结

高偏差和高方差的一些解决方案

神经网络中的应用

神经网络是低偏差的模型，
在训练过程中如果Jtrain 过大可以使用更大的神经网络，缺点就是运算速度会变低且会增加研发成本
在Jtrain 基本与基准线相差不大时计算Jvc，如果Jvc 过大可以增加数据样本重新回到模型计算
经过上面不断重复的过程，最终得到合适的模型参数

只要数据规则化做的合适，大型神经网络总是会比小型神经网络表现好一些

在tensorFlow 中，可以在构建layer 时传入规则化参数

练习

练习多项式，正则化参数𝜆，训练数据个数m, 神经网络层数
链接

The simple model is a bit better in the training set than the regularized model but it worse in the cross validation set.

Adam Algorithm

一种加快模型学习的优化算法
可以自动调节学习率的大小，使模型更快的朝梯度下降的方向学习

卷积层

之前讨论的神经网络中的中间层，都依赖上一层所有的输出进行计算
Each neuron output is a function of
all the activation outputs of the previous layer.
有一种计算方案是只选取上一层的部分数据计算本层的输出
这种layer 被称为卷积层（Convolutional Layer）
优点有两个
一个是可以加快计算，
另外一个是可以减少需要的训练数据

降低预测结果错误率

拿到训练模型后，如果遇到一个不可接受的错误输出，可以通过以下方式进行重新调整

更常见的方式是用诊断的方式评估模型好坏
在训练前将数据分成两组，
一组用于模型训练，称为训练组
另一组用于测试训练得到的模型，称为测试组

比如对于过拟合的情况
将数据分成两组

分别计算训练组和测试组的损失函数

对于训练组数据的损失函数肯定会更小
要关注的是测试数据的损失函数，值越小，说明越近真实的值，说明模型越好
上面是线性回归模型，下面是对于分类问题的损失函数计算

如果需要在多个模型间进行选择，可以在一开始的时候将数据分成三组
训练组，交叉验证组，测试组

同样计算基于交叉验证组数据的损失函数，值越小说明越符合实际数据
主要作用是用于选择模型，比如挑出最合适的多项式

然后再使用测试组数据进行泛化错误的测试

Softmax regression

之前的二分类问题用logic regression 可以解决，
但是对于多分类问题，可以在此基础上，遵循所有可能性加和为1的原则
进行扩展

假如现在需要判断4种可能性的概率
那我们需要四条分界线（如下图在z1-z4）
然后通过通过下面这个公式

计算得到a1 - a4
就可以得到4种可能性的概率

这种算法就是 Softmax regression

损失函数

参照逻辑回归函数的损失函数
假如y = 1, 那么损失函数就是

y = 0 的话损失函数就是

归纳一下就是，当y = an时
损失函数就是Loss = -log(an)
因为 y 只能可能是a1-an N 种可能性中的一种
下面的Loss趋势图说明，当an 值越接近1 的时候 损失函数越小
也就是说a1 - an 这些概率值越接近1 损失函数越小
相当于概率值对应的可能性越可能接近真实y值，越准

在神经网络中使用

之前的二分类问题中，在神经网络的最后一层使用sigmoid 函数作为输出函数（或者激活函数）可以识别图片中的 0 和 1
现在如果要识别图片中的数字是0-9 10种分类中的哪一种，
要做的就是将输出层激活函数换成softmax 函数，并且是10个节点就可以实现
每个节点代表一种可能，值最大的就是可能性最大的值

tensorFlow 中实现

方案1

不推荐，用方案2优化

方案2

原因是在tensorFlow 中使用中间步骤计算数值和直接将式子带入计算最终值的处理过程不同，tensorflow 会对后者重新排列表达式中的术语
并想出一种更准确的计算方式去计算，方案二在方案一基础上做的修改就是在将式子带入计算，而不是先计算中间值，再带入

区别多标签多分类问题

上面讨论的是多分类问题，一个问题多个可能性
多标签多分类问题是指同时推测多个问题的多个可能性

计算方式可以是分别看成单个神经网络计算，一个神经网络处理一个问题的多种可能
也可以同时计算，输出多个问题对应的多个可能

什么是神经网络

类似于大脑中的神经元传递信息的过程，将多个输入通过多层模型处理后得到结果输出的架构，就是神经网络

复杂神经网络的表示

从预测手写数据0和1 的过程，理解神经网络向前传播的计算原理

The parameters have dimensions that are sized for a neural network with 25 units in layer 1, 15 units in layer 2 and 1 output unit in layer 3.
the dimensions of these parameters are determined as follows:
If network has 𝑠𝑖𝑛 units in a layer and 𝑠𝑜𝑢𝑡 units in the next layer, then
𝑊 will be of dimension 𝑠𝑖𝑛×𝑠𝑜𝑢𝑡 .
𝑏 will a vector with 𝑠𝑜𝑢𝑡 elements
Therefore, the shapes of W, and b, are
layer1: The shape of W1 is (400, 25) and the shape of b1 is (25,)
layer2: The shape of W2 is (25, 15) and the shape of b2 is: (15,)
layer3: The shape of W3 is (15, 1) and the shape of b3 is: (1,)
Note: The bias vector b could be represented as a 1-D (n,) or 2-D (n,1) array. Tensorflow utilizes a 1-D representation and this lab will maintain that convention.

向前传播：从左到右计算，根据输入计算出输出，输出即预测结果，

使用tensorflow 实现向前传播的神经网络

具体实现

Tensorflow models are built layer by layer. A layer’s input dimensions ( 𝑠𝑖𝑛 above) are calculated for you. You specify a layer’s output dimensions and this determines the next layer’s input dimension. The input dimension of the first layer is derived from the size of the input data specified in the model.fit statment below.

Note: It is also possible to add an input layer that specifies the input dimension of the first layer. For example:
tf.keras.Input(shape=(400,)), #specify input shape
We will include that here to illuminate some model sizing.

调用numpy()方法可以实现张量和numpy matrix 之间的转换

使用tensorflow 实现神经网络的另外一种架构形式

The model.compile statement defines a loss function and specifies a compile optimization.
The model.fit statement runs gradient descent and fits the weights to the data.

图片识别0和1练习

神经网络的训练过程

如何选择激活函数

常见的三种激活函数

选择激活函数的一般规则
对于输出层，根据输出值来
如果是二分类问题，使用sigmoid
如果是输出正负值都有就选则线性激活函数
如果输出值非负，那么 就使用ReLu函数
对于中间层，一律使用ReLu函数
原因有三

1. 一个是作为激活函数，本身计算过程比sigmoid 函数简单
2. relu只有在小于0 的时候斜率为0，sigmoid 函数在趋向正负无穷的时候有两处斜率趋近0 的情况，会导致梯度下降计算过程变慢，所以ReLu函数在梯度下降过程相比之下会更快一些
3. 如果在隐藏层使用线性激活函数，输出层是sigmoid函数，整个过程等同于线性回归，最终始终会变成二分类的结果

什么是过拟合

训练得到的预测模型对于每个训练数据都非常吻合，导致对于新的测试数据无法正确评估的现象，就是过拟合
下面是线性回归和逻辑回归模型三种训练结果的展示

解决办法

1. 收集更多的数据进行训练
2. 选择和使用有价值的特性值参与运算
3. 减小部分特征值(对于结果预测关系不大的特征值)的参数值（正则化）

正则化

在成本函数或者损失函数中增加正则化参数，避免过拟合

在梯度下降计算过程中，会使得每个参数在原来基础上乘以一个比1小的数据再去进行减法运算，从而使得梯度下降过程中实现参数进一步缩小

cost and gradient functions for both linear and logistic regression. Note:

Cost

The cost functions differ significantly between linear and logistic regression, but adding regularization to the equations is the same.

Gradient

The gradient functions for linear and logistic regression are very similar. They differ only in the implementation of $f_{wb}$.

线性回归正则化

逻辑回归正则化

实践案例

背景&&解决问题

逻辑回归模型时一种解决二分类问题的算法

如果用线性回归去解决分类问题，会导致过拟合出现，每增加一个测试数据，都可能导致模型发生变化

通过使用sigmoid function函数，设置阈值，可以将线性回归产生的结果归类到两个结果上去

虽然目标是二分类，即结果只能是0 或者1
但是f(w,b) = g(w·x+b) 计算的结果值A只能无限接近这两个值
这里可以将A理解成结果是1 的可能性

决策边界

在逻辑回归模型f(w,b) = g(w·x+b) 中
z = w·x+b 又称为 决策边界，将不同结果的数据在坐标系中进行隔离
如果特征在z 中没有多项式运算，那么，得到的边界必定是直线的，但是如果有多项式，拿得到的边界线就是非线性的

成本函数

线性回归的平方误差算法的成本函数在应用到逻辑回归时，会产生多个局部最小值，再用梯度下降的算法去找参数时，无法找到最小值

逻辑回归引入逻辑损失函数，根据单个数据集随参数变化的趋势，判断整体的变化趋势
操作就是将原本平方误差除以2的操作移到求和之前，单独计算每个特征值的部分就是损失函数

Logistic Regression uses a loss function more suited to the task of categorization where the target is 0 or 1 rather than any number.

these definitions are used:

Loss is a measure of the difference of a single example to its target value while the

Cost is a measure of the losses over the training set

下面是推导过程和最终的式子

梯度下降找到w&b

一些专业术语表达

x–> 训练数据入参，特征值，这里仅有一个，这个模型也被叫做 单变量线性回归模型 x(i) 第i个训练数据的x
y–> 训练数据入参，标记值， example 的lable ,y(i) 第i个训练数据的y
y-hat –> 出参，推测值, 模型（f（x）= wx + b） 的 结果值

成本函数

平方误差成本函数

在f(x) = wx+ b 的模型中
w: 斜率
b: 截距，intercepter 直接与Y轴交点距离远点距离

用J(w,b)表示成本函数，找到能够使J(w,b) 的值最小的w和b，就可以找到使f(x)最接近所有测试集的模型，最拟合训练数据的模型
先讨论在b = 0 的情况下，j（w） 随w 变化的趋势

找到使j(w) 最小的w,即U形线最凹的地方

现在把b的变化趋势也加入讨论，j(w,b) 随w，b 变化的趋势，将变成3d 的碗状

最凹的地方就是J(w,b)值最小的地方

利用等高线的表达方式，换一种视角找J(w,b)的最小值，就是将3D 图进行水平切割，得到关于w,b 的二维椭圆视图
不同(w,b) 组合可能会落在在同一条线上的，相同线上的J(w,b)值一样大
所以能够使J(w,b)值最小的(w,b)值，就是同心圆里面最里面那个圆上的多对(w,b), 当圆极限到一个点时，就只有一对(w,b)使J(w,b)最小

GradientDescentAlgorithm 梯度下降算法

是一种寻找使成本函数达到最小值参数的通用算法，现在不再局限与于f(x) = wx+b 单变量线性模型
对于多变量模型，也就意味着多个w, 这样J(w,b) 就会变成J(w0,…wi,b), J(w0, …wi) 的趋势不再是U形

梯度下降指的是，从一个点出发，环顾四周，找到能够下降的谷底的最快的方向，即梯度最陡的方向，下降一步，每走一步都按最陡方案下降，从而实现最快到达谷底的目的
达到谷底即意味着找到J(w0,…wi,b)最小值
但是梯度下降有一个特性，就是，虽然从同一点出发，如果第一步选择反向不同，或者走的方式不同，肯定会到达不同谷底
不同谷底意味着不同的J(w0,…wi,b)最小值，这些最小值，都叫做局部最小值

算法实现与理解

J(w,b)关于w 导数 表征 U形趋势线上随w 变化的梯度值，也就是斜率
前面的系数α表征 下坡的步伐大小 是一个0-1 的正小数值，称为学习率
w,b 同时变化，同时更新

当梯度大于0时，temp_w 逐渐变小，J(w,b) 的值也逐渐变小
当梯度小于0 时，temp_w 逐渐变大（负斜率，绝对值在变小）， J(w,b)的值逐渐变小
说明J(w,b) 的值随梯度的变化符合随w的变化趋势
当斜率绝对值逐渐变小时，就是都朝J(w,b) 最小值聚拢

实验

关于学习率

太小会增加计算步骤，从而使梯度算法变慢
太大可能导致过冲，永远无法到达最小值;甚至无法实现聚拢趋势，导致发散

局部最小值

如果当前参数已经使得成本函数到达一个局部最小值，那么J(w,b) 关于w 导数值将会是0，那么temp_w 会始终停留在一个固定的值，不再变化
梯度下降算法将不会再进行下一步的计算，保持当前参数在当前的这个一个局部最小值的状态

随这个梯度下降，我们可以知道我们正在朝成本函数最小值靠近，在学习率固定情况下，更新步骤也在下降(斜率本身朝0在逐渐变小)，说明没有学习率的变化，也能到达局部最小值
但如果同时将学习率调小，降低下降的步伐，可以更小幅度的一点点接近最小值，最终找到成本函数最小值

小结

线性回归模型，成本函数，和梯度下降算法


上述梯度下降算法具体来说是批量梯度下降，因为每一步都用到了所有训练数据

多元线性回归

以上讨论的是只有一个特征值x 作为输入的情况，下面要讨论的是同时有n个特征值做输入的模型，被称为多元线性回归模型

一些符号的表示方法

模型表达式

向量化

好处

1. 代码实现简洁
2. 运算速度快

对于多元线性回归 的 梯度下降算法

w 相关的计算转成向量计算，不同权重值，取对应特征值进行计算

实验

实践技巧

如何更快的找到合适的参数去拟合训练集

特征缩放

参数大小与特征值大小关系

如果某一特征值(x1 属于[1000,5000]范围)相对其他特征值(x2,x3,..xn,属于[1,10]范围),数值范围较大，其对应参数w1 则相对其他较小
反之，如果特征值较小，则参数较大，这样的规律可以更快的找到适合的参数


如果特征值的取值范围非常不同时，会导致梯度下降速度变慢
但如果将所有特征值想办法归一到相同的范围内，就可以加快梯度下降过程，降低计算步骤

缩放计算方式

除以最大值

特征值除以各自范围的最大值

均值归一化

特征值 减去平均值，再除以极差值(范围最大值减去范围最小值)

Z-SCORE归一化

特征值 减去 标准差，除以 平均值

说明

并不一定非要落在-1 到1 之间，落在相同的数量级之间就可接受

如何找到成本函数最小值

学习曲线

绘制成本函数随迭代次数变化的趋势图，称为学习曲线，主要是根据曲线走势判断梯度是否在收敛
如果随迭代次数增加，成本函数一直呈下降趋势，说明梯度正在下降，是正常的
当下降到一定程度，随迭代次数成本函数不再有明显下降，说明梯度收敛到了极限，也就是找到了成本函数的最低点
但如果随次数增加，成本函数出现上升，这是不正常的，则说明学习率选取过大，需要重新选取，或者代码出现错误

自动收敛测试

自行定义一个极小的值，当某次迭代后成本函数值小于该值时，就认为梯度下降关闭，成本函数达到最小值，停止迭代，取当前迭代wb做模型参数
缺点就是极小值难以估计，且结果不太可靠

如何选择合适学习率

根据学习曲线调整学习率
学习率太大会导致学习曲线出现上升趋势
太小会导致迭代次数增加

可以先对不同量级的学习率进行测试，观察学习曲线变化快慢
然后进行N倍测试，再比较，通过多组测试观察学习曲线变化快慢进行选取

特征工程

通过转换或者合并直接(原始)的特征值，生成新的特征值进行模型训练

多项式回归

如果特征值只有一个的情况下，不希望得到线性回归的直线模型，希望用曲线去拟合训练集
可以采用下面两种方法去拟合

1. 通乘方构建新特征值，但是在进行训练时要进行归一化处理，因为乘方处理后，各个特质值范围的数量级会变得不同
2. 通过开方进行新特征值构建
   

如何在colab中运行github 上的jupiter文件

下面这个链接时梯度下降实现的.ipynb 文件

https://github.com/kaieye/2022-Machine-Learning-Specialization/blob/main/Supervised%20Machine%20Learning%20Regression%20and%20Classification/week1/work/C1_W1_Lab05_Gradient_Descent_Soln.ipynb

复制域名之后的path
kaieye/2022-Machine-Learning-Specialization/blob/main/
Supervised%20Machine%20Learning%20Regression%20and%20Classification/week1/work/C1_W1_Lab05_Gradient_Descent_Soln.ipynb
拼接到 https://colab.research.google.com/github/ 后面

得到访问链接

https://colab.research.google.com/github/kaieye/2022-Machine-Learning-Specialization/blob/main/Supervised%20Machine%20Learning%20Regression%20and%20Classification/week1/work/C1_W1_Lab05_Gradient_Descent_Soln.ipynb

如果.ipynb有依赖其他py 文件，可以点击上传图标直接上传

但是要注意这里上传的文件都是运行时的状态，页面关闭即销毁，
如果想要保存自己修改后的.ipynb文件可以通过添加副本到google/drive 来实现

什么是机器学习

filed of study that gives computers the ability to learn without being explicity programmed.

让计算机在没有明确编程的情况下学习的研究领域

– Arthur Samuel (1959)

Supervised Learning 监督学习

learns from being given ‘right answers’

learns from data labeled with ‘right answers’

regression algorithms 回归算法

从无限多可能数字中预测数字

predict a number 预测无限可能中的一种
infinitely many possible outputs

classify algorithms 分类算法

predict categories 预测有限分类中的一类
small number of possible outputs

Unsupervised Learning 无监督学习

find sth interesting in unlabeled data
data only comes with input x ,but not output labels y, algorithm has to find structure in the data

clustering algorithms 聚类算法

place the unlabeled data (automatically group) into different clusters

eg. google news, grouping customers

==> group similar data points together

Anomaly detection 异常检测

find unusal data points (events)

eg. 金融诈骗中的交易异常

Dimensionality reduction 降维算法

compressn data using fewer numbers

压缩大数据集到小数据集，同时丢失尽可能少的信息

Reinforcement Learning 强化学习

todo 下载 代码，看原理流程，运行耗token, 测试