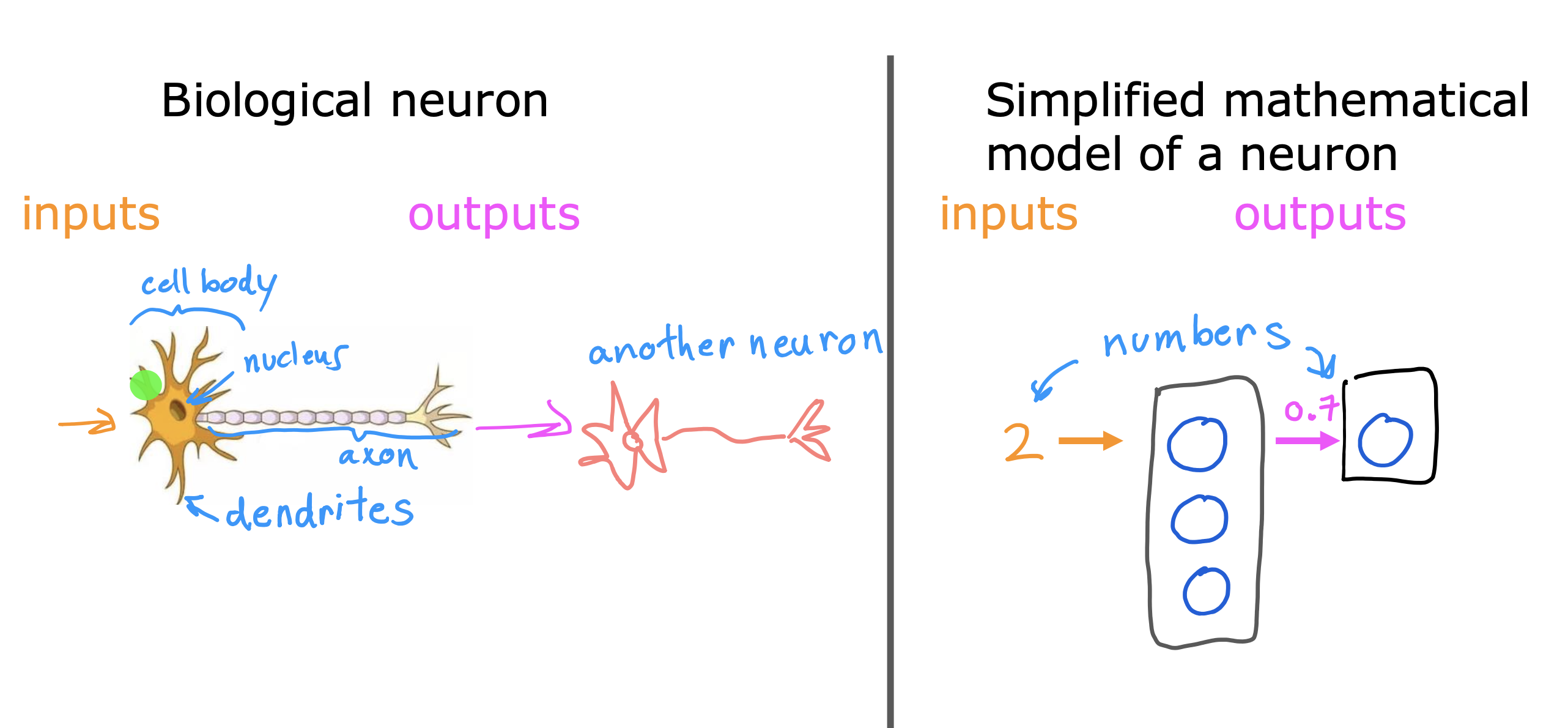
什么是神经网络
类似于大脑中的神经元传递信息的过程,将多个输入通过多层模型处理后得到结果输出的架构,就是神经网络
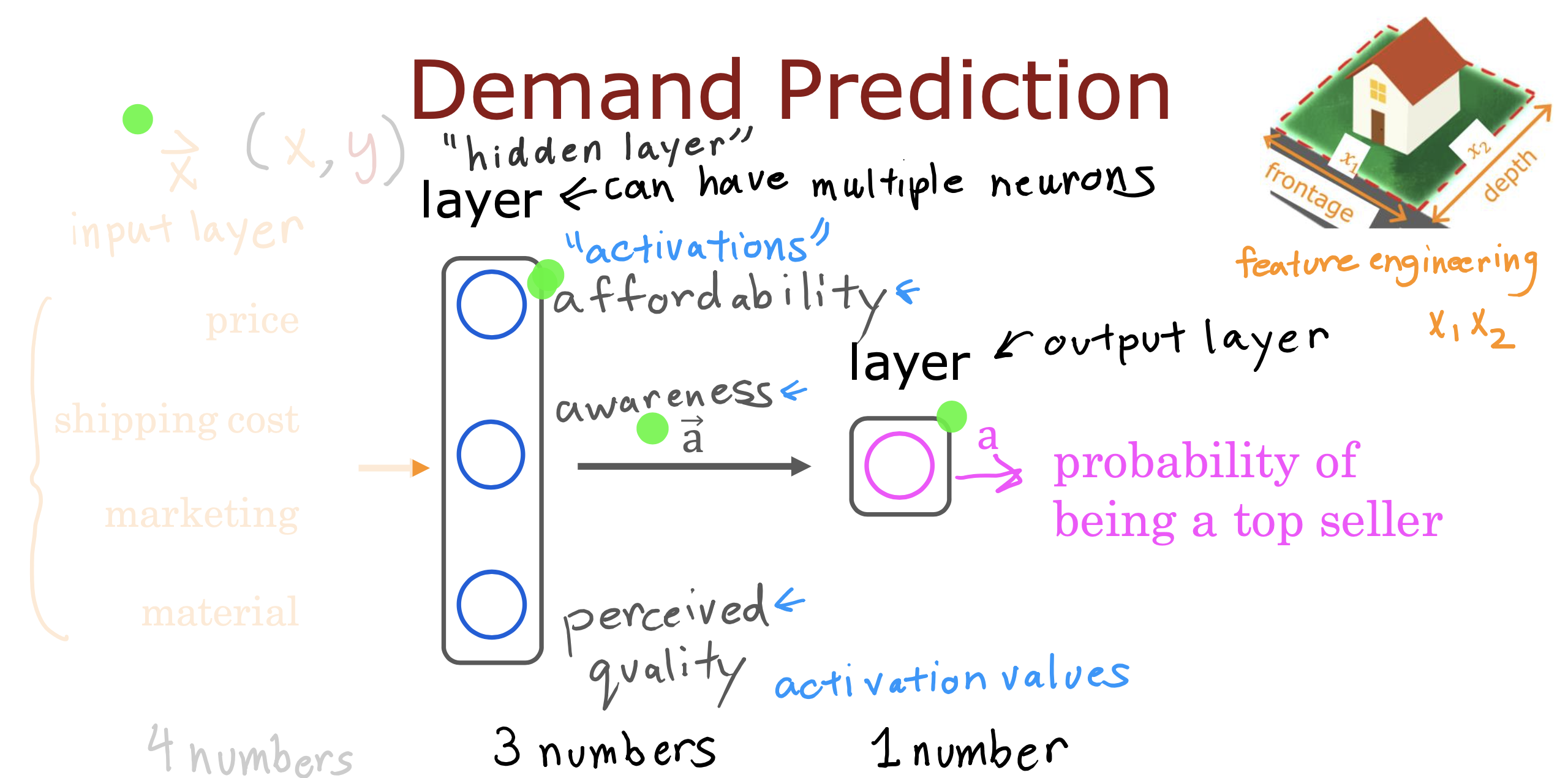
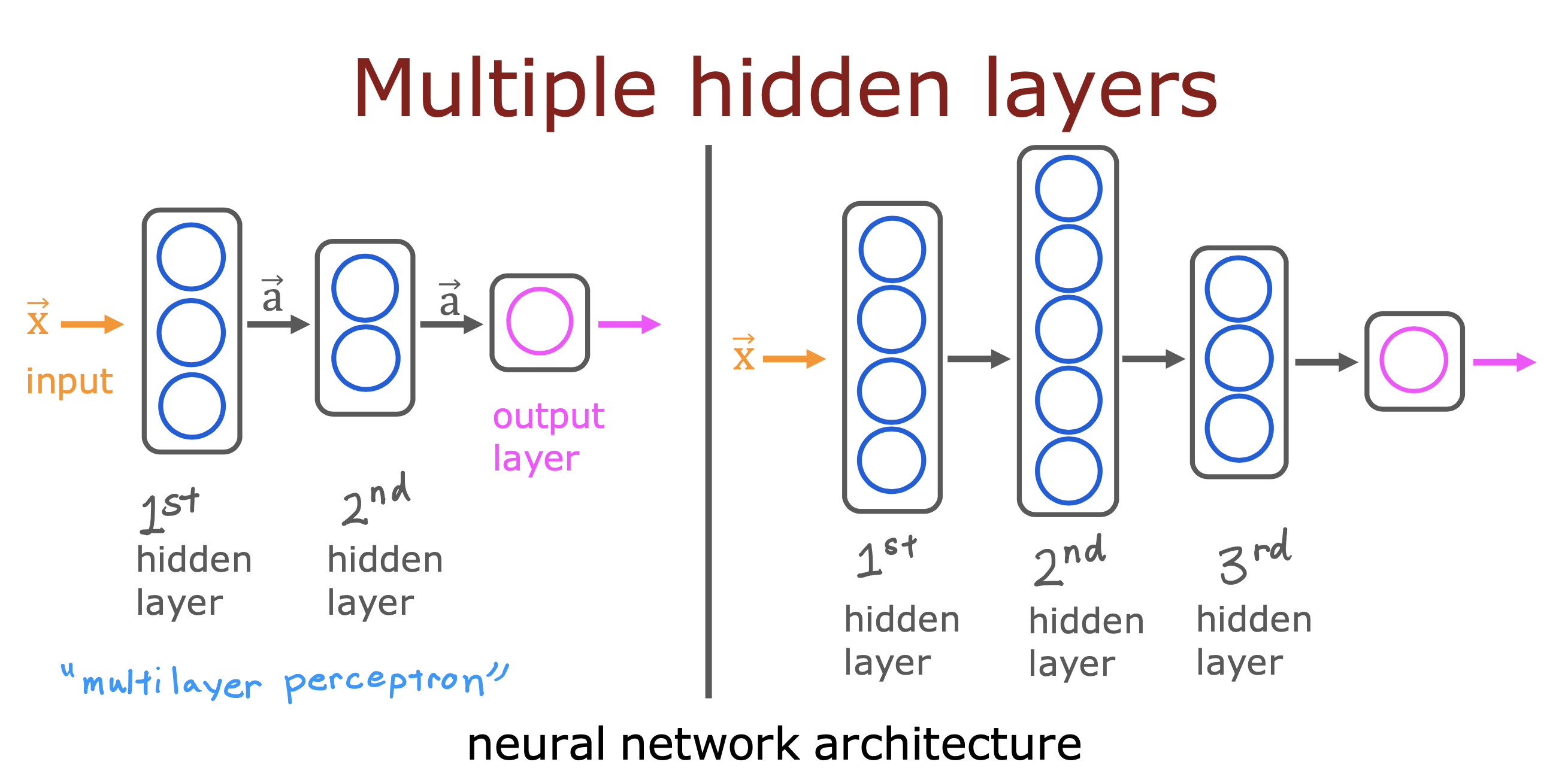
复杂神经网络的表示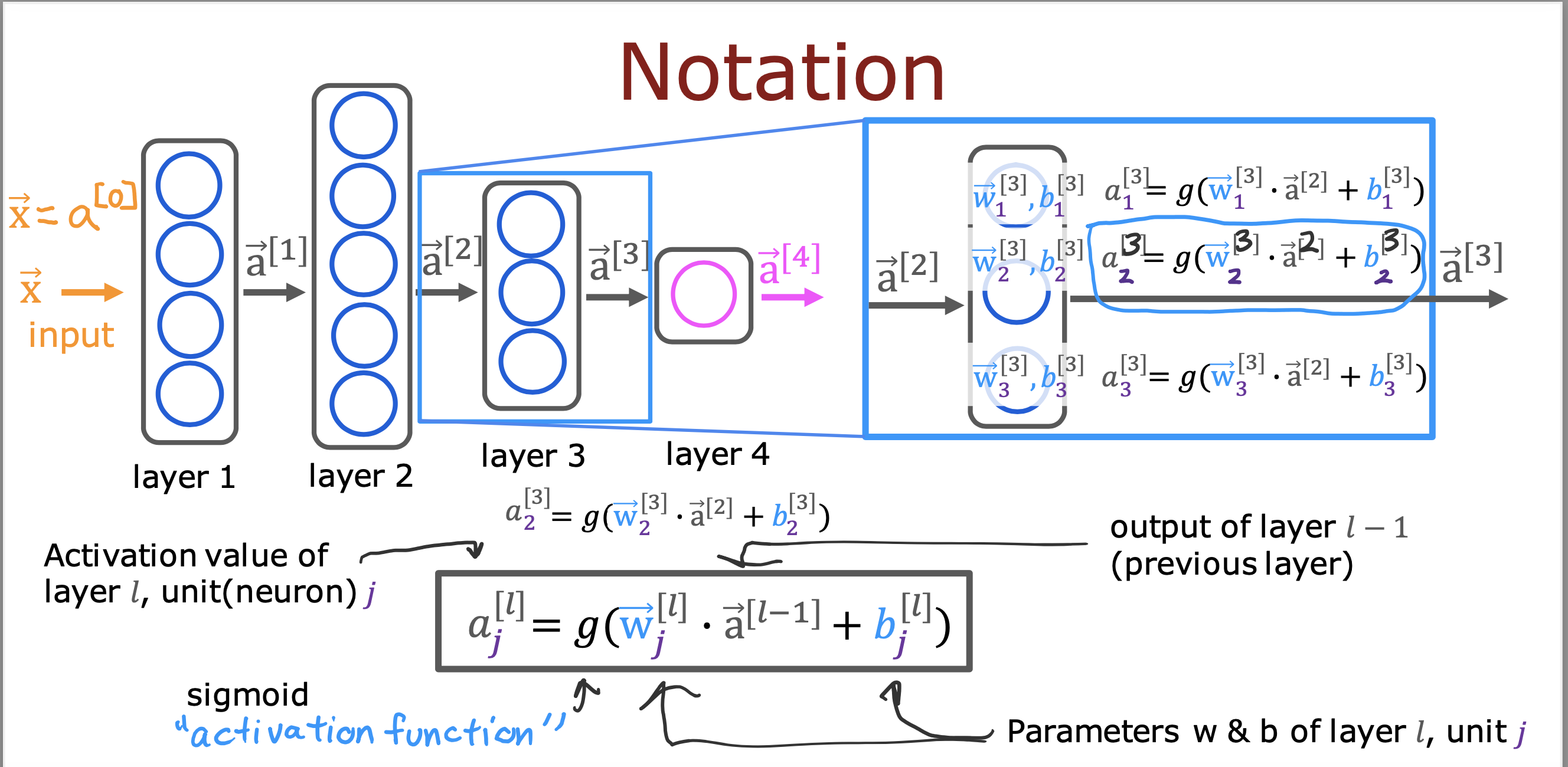
从预测手写数据0和1 的过程,理解神经网络向前传播的计算原理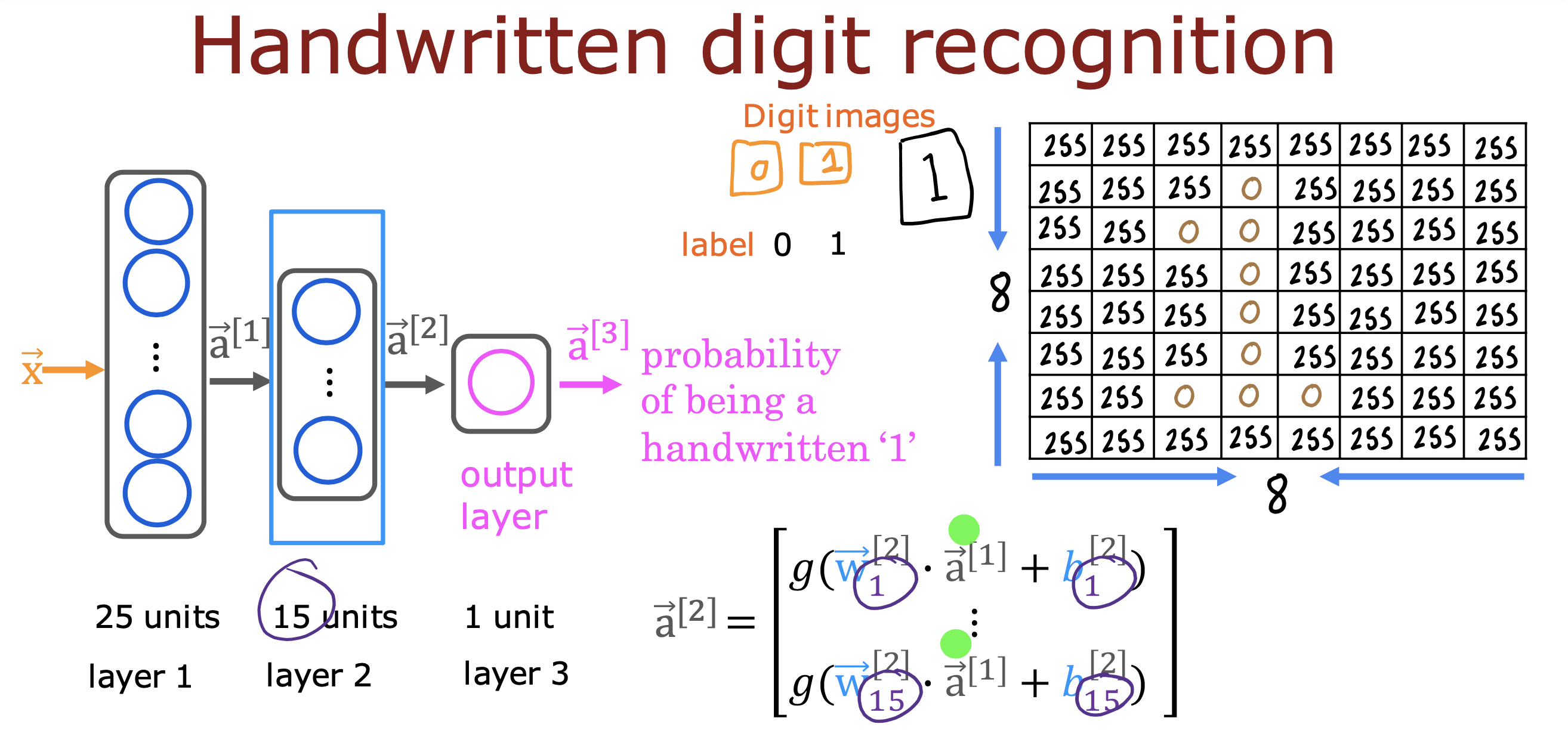
The parameters have dimensions that are sized for a neural network with 25 units in layer 1, 15 units in layer 2 and 1 output unit in layer 3.
the dimensions of these parameters are determined as follows:
If network has 𝑠𝑖𝑛 units in a layer and 𝑠𝑜𝑢𝑡 units in the next layer, then
𝑊 will be of dimension 𝑠𝑖𝑛×𝑠𝑜𝑢𝑡 .
𝑏 will a vector with 𝑠𝑜𝑢𝑡 elements
Therefore, the shapes of W, and b, are
layer1: The shape of W1 is (400, 25) and the shape of b1 is (25,)
layer2: The shape of W2 is (25, 15) and the shape of b2 is: (15,)
layer3: The shape of W3 is (15, 1) and the shape of b3 is: (1,)
Note: The bias vector b could be represented as a 1-D (n,) or 2-D (n,1) array. Tensorflow utilizes a 1-D representation and this lab will maintain that convention.
向前传播:从左到右计算,根据输入计算出输出,输出即预测结果,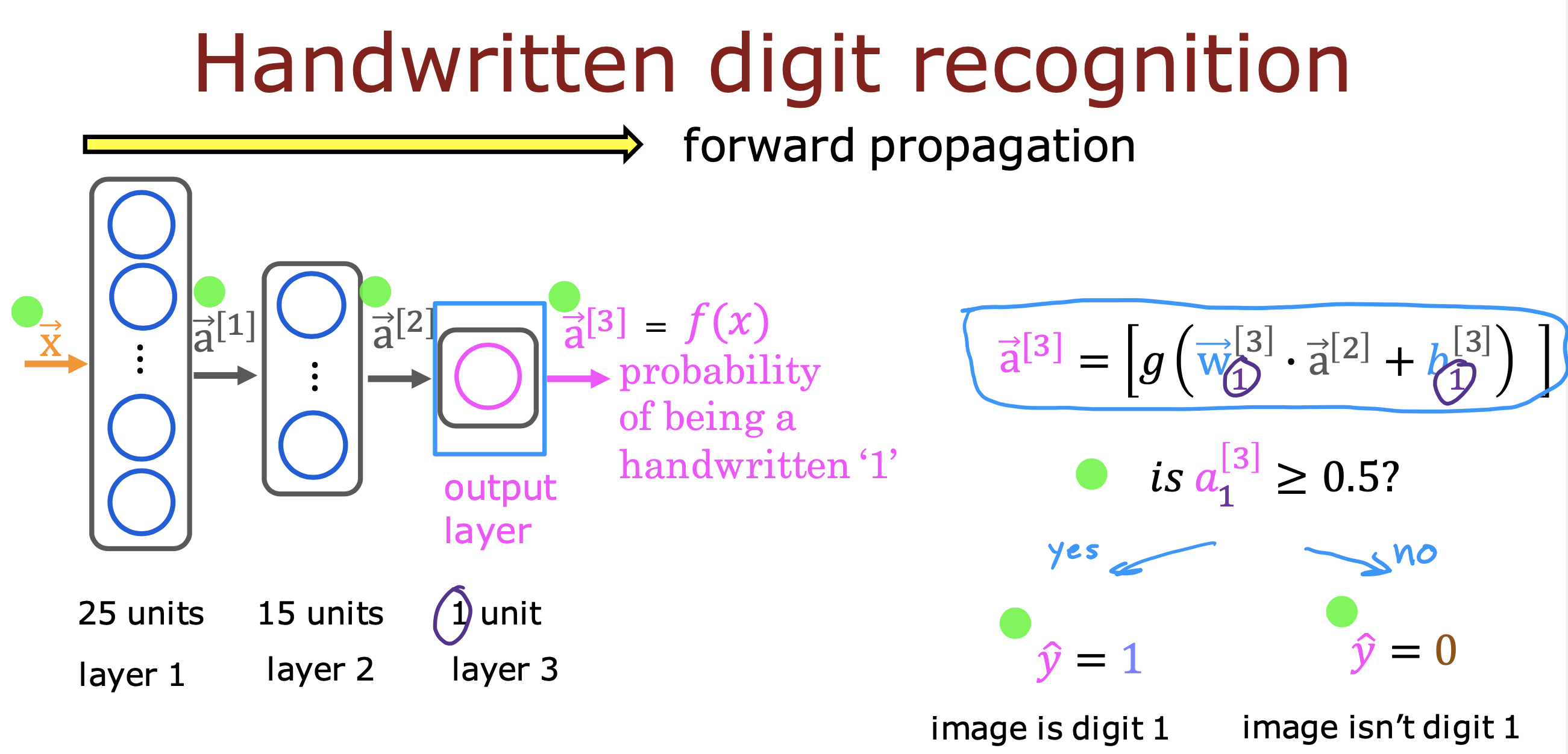
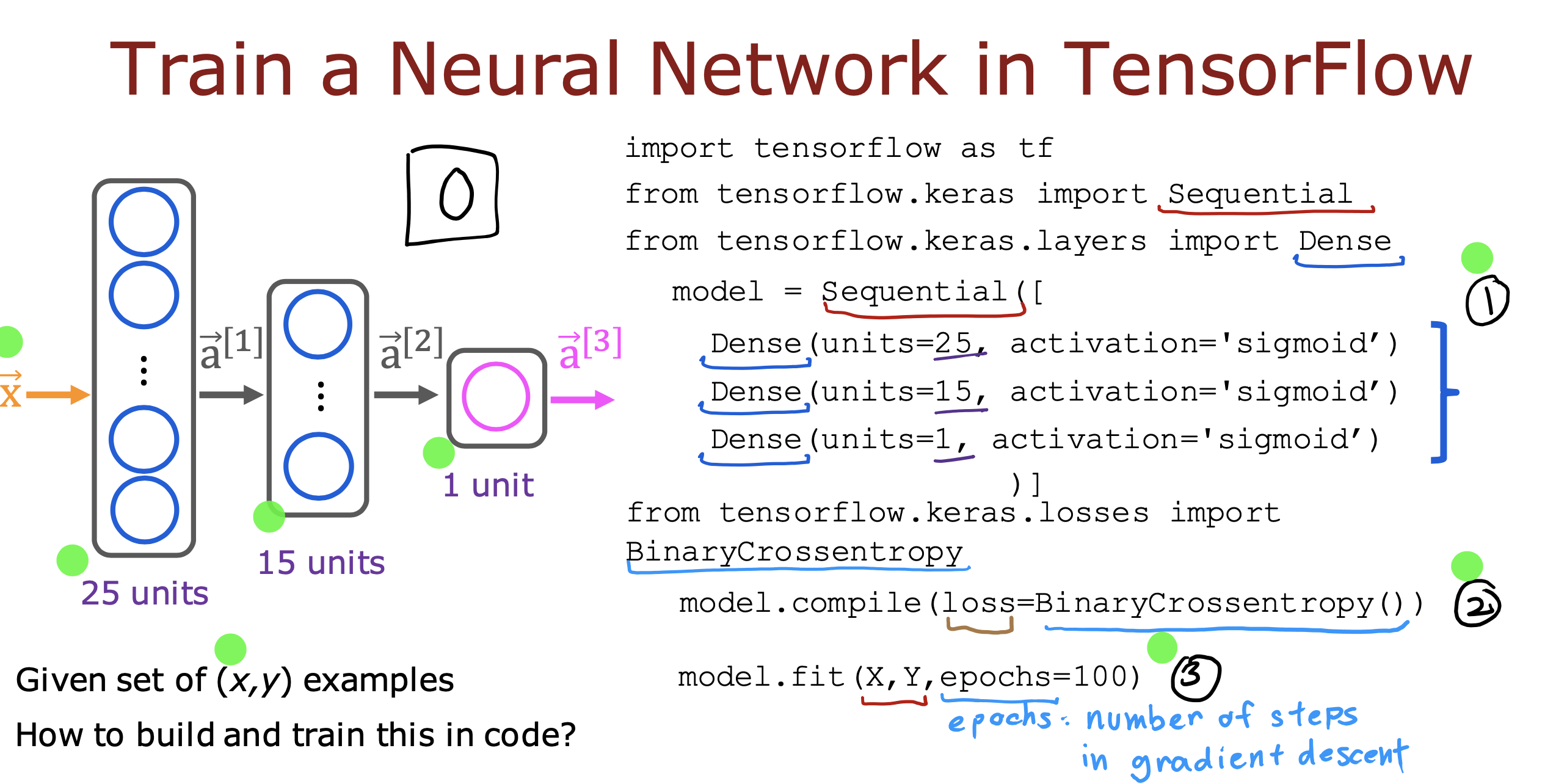
使用tensorflow 实现向前传播的神经网络
具体实现
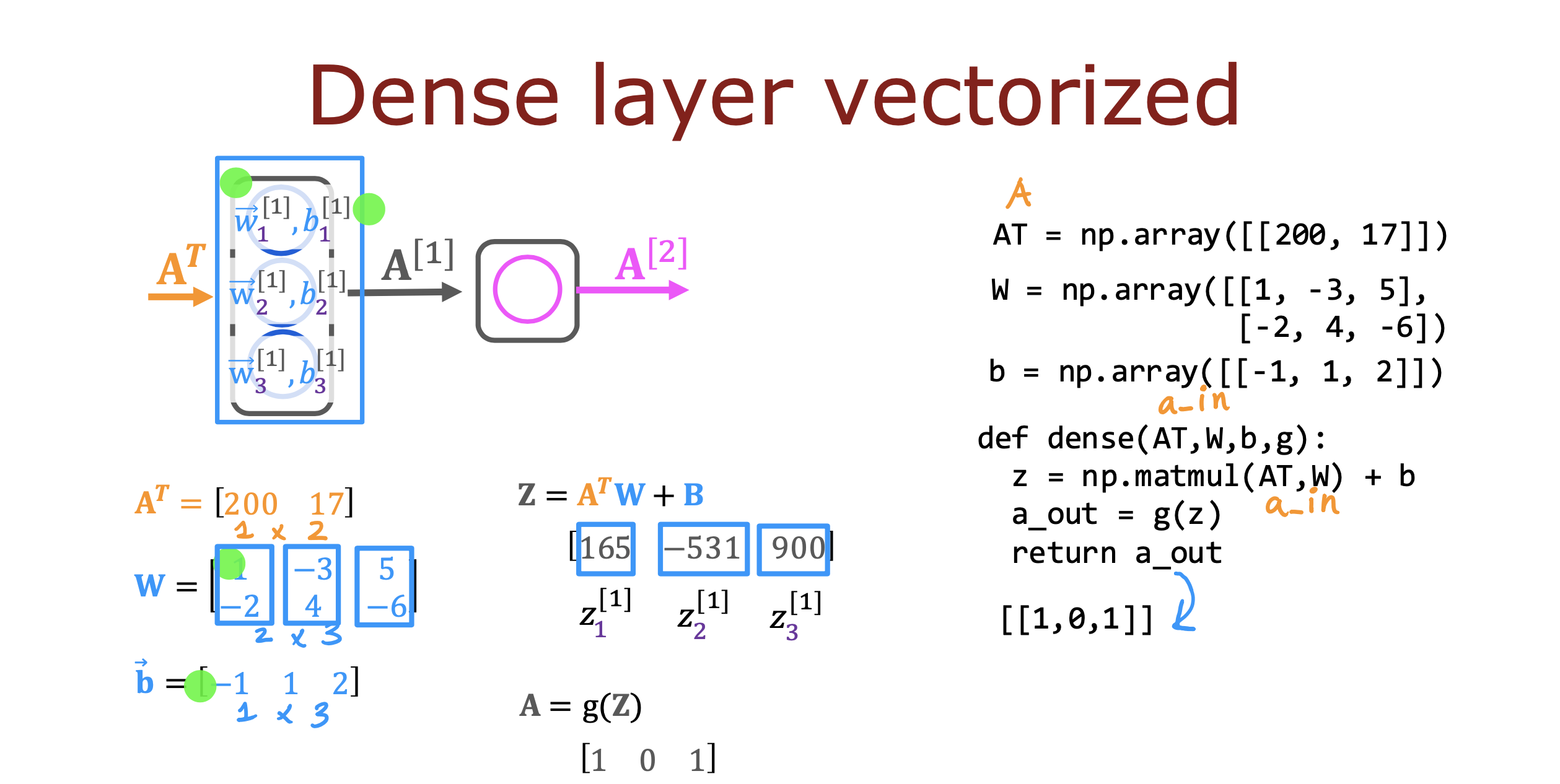

Tensorflow models are built layer by layer. A layer’s input dimensions ( 𝑠𝑖𝑛 above) are calculated for you. You specify a layer’s output dimensions and this determines the next layer’s input dimension. The input dimension of the first layer is derived from the size of the input data specified in the model.fit statment below.
Note: It is also possible to add an input layer that specifies the input dimension of the first layer. For example:
tf.keras.Input(shape=(400,)), #specify input shape
We will include that here to illuminate some model sizing.
调用numpy()方法可以实现张量和numpy matrix 之间的转换
使用tensorflow 实现神经网络的另外一种架构形式
The model.compile statement defines a loss function and specifies a compile optimization.
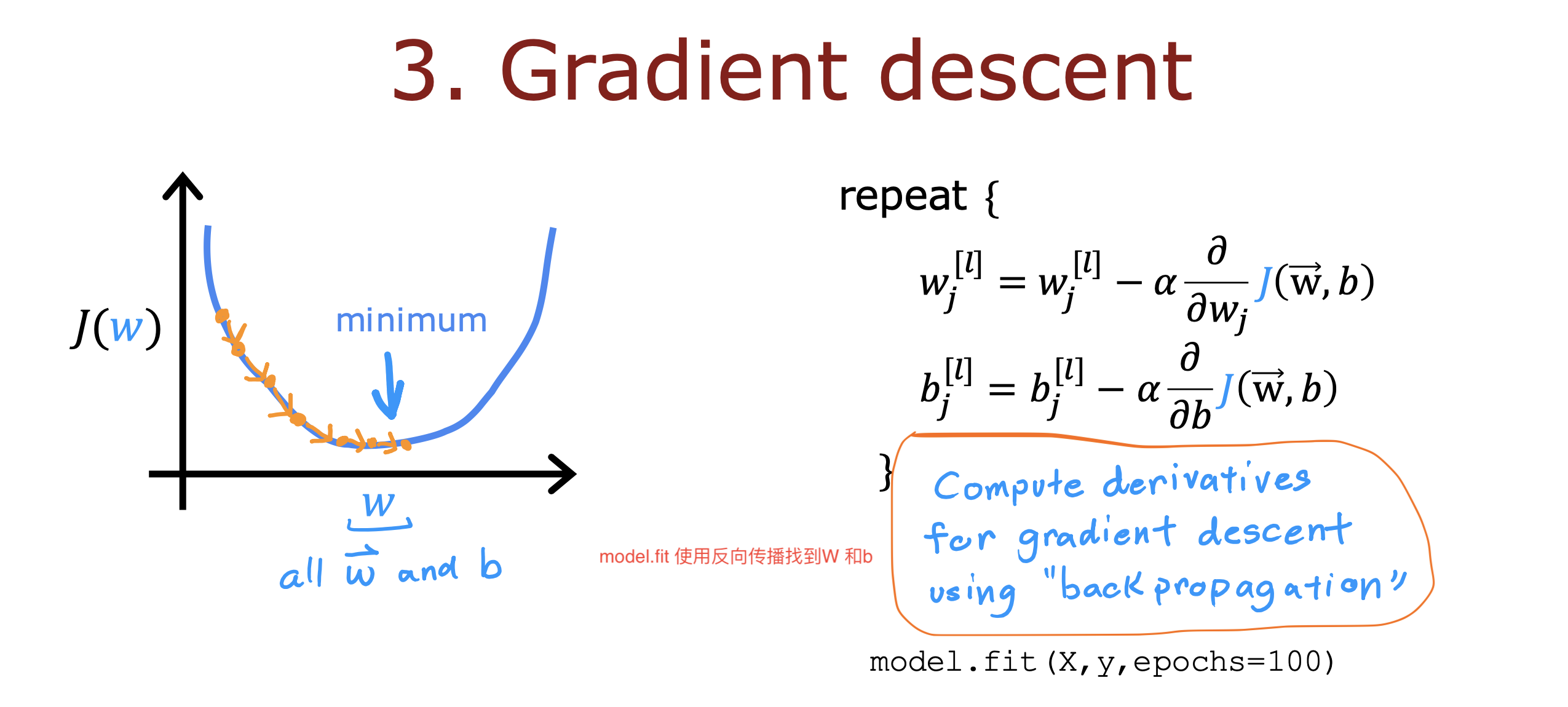
The model.fit statement runs gradient descent and fits the weights to the data.
神经网络的训练过程




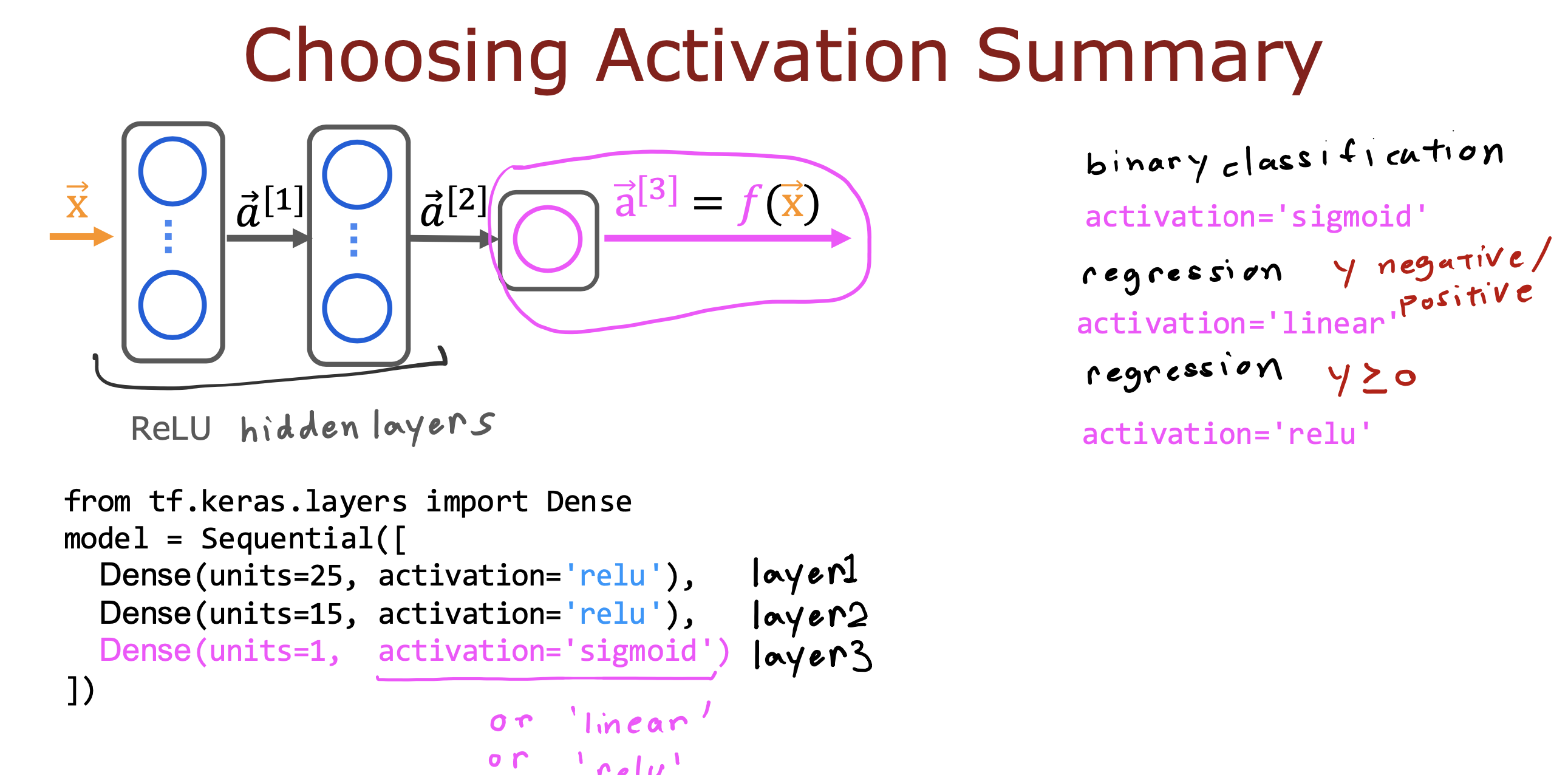
如何选择激活函数
常见的三种激活函数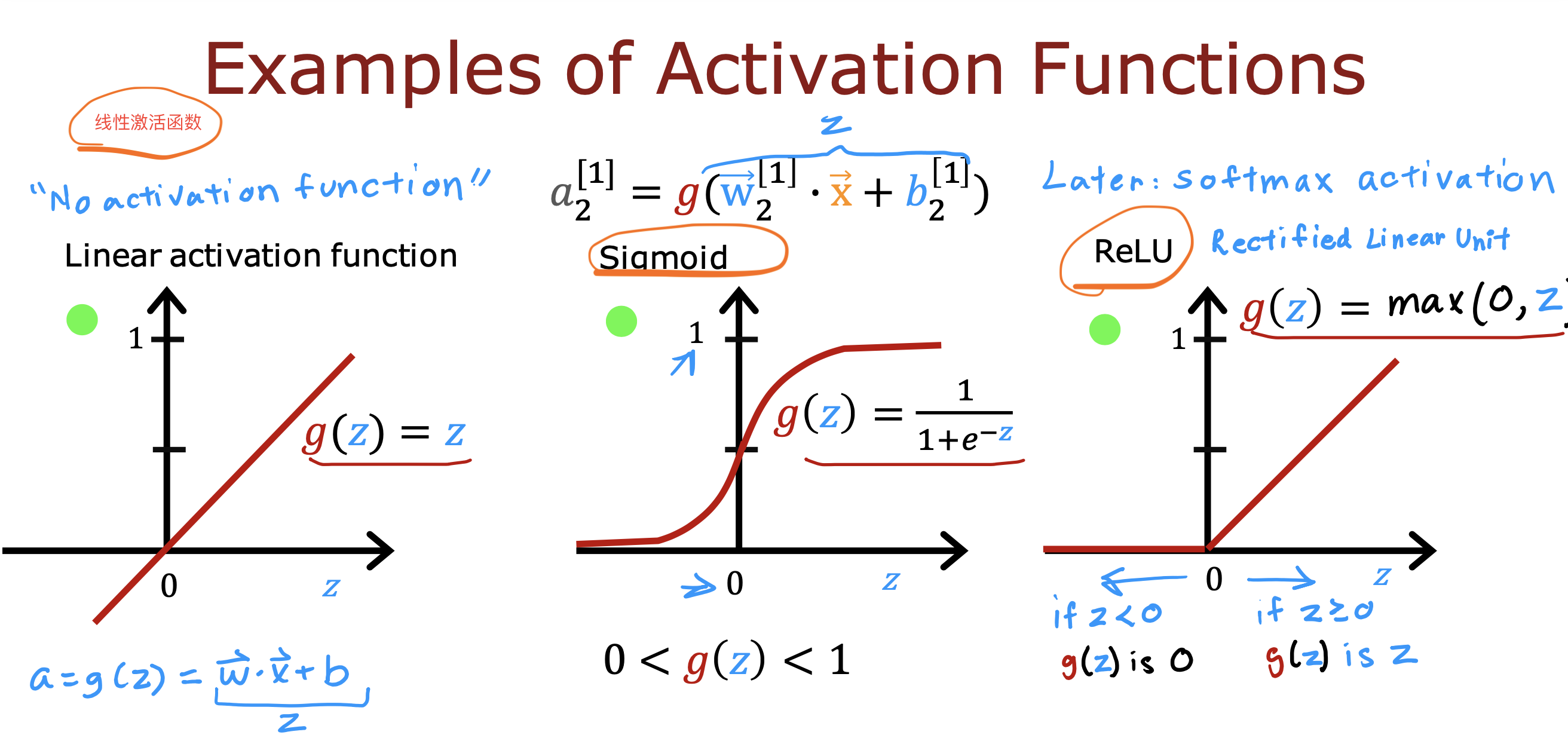
选择激活函数的一般规则
对于输出层,根据输出值来
如果是二分类问题,使用sigmoid
如果是输出正负值都有就选则线性激活函数
如果输出值非负,那么 就使用ReLu函数
对于中间层,一律使用ReLu函数
原因有三
- 一个是作为激活函数,本身计算过程比sigmoid 函数简单
- relu只有在小于0 的时候斜率为0,sigmoid 函数在趋向正负无穷的时候有两处斜率趋近0 的情况,会导致梯度下降计算过程变慢,所以ReLu函数在梯度下降过程相比之下会更快一些
- 如果在隐藏层使用线性激活函数,输出层是sigmoid函数,整个过程等同于线性回归,最终始终会变成二分类的结果