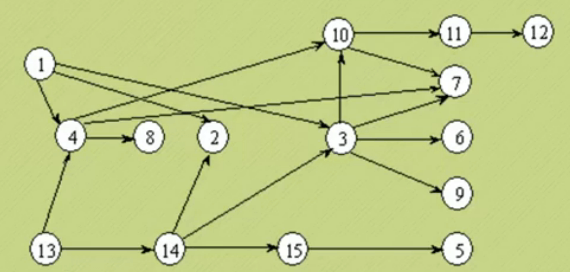
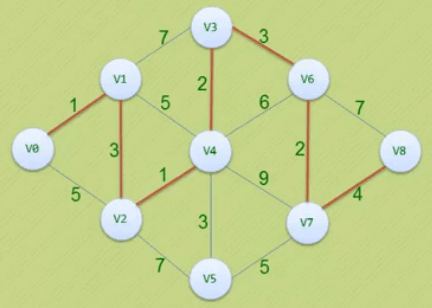
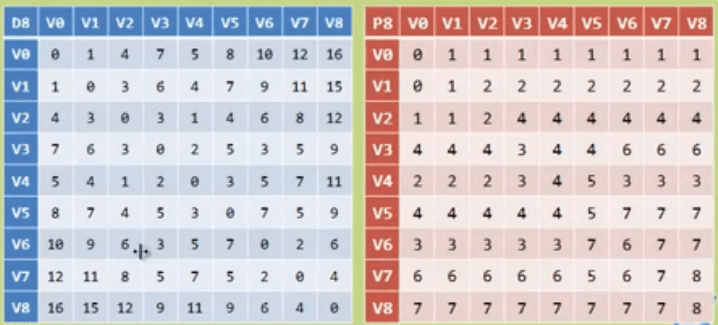
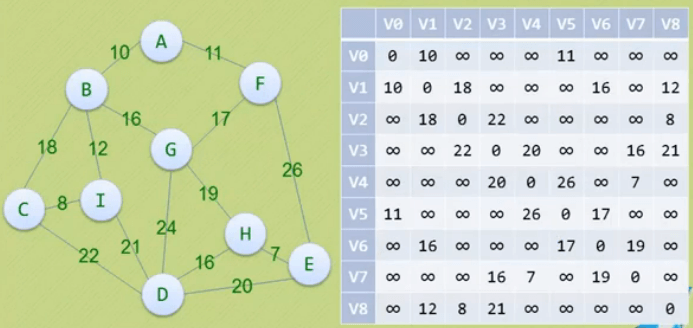
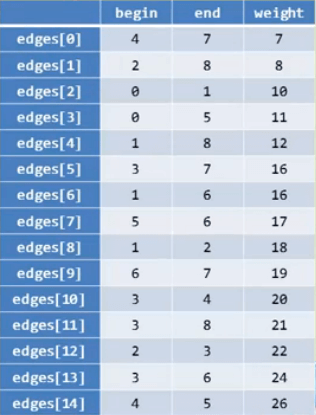
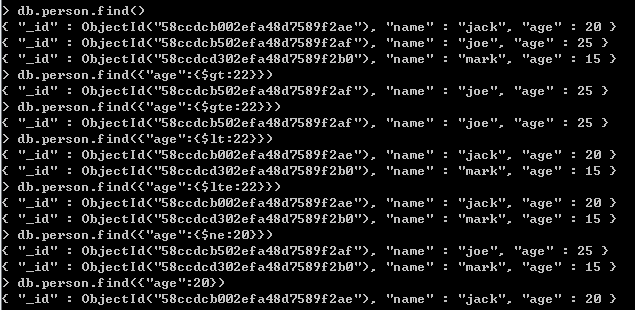
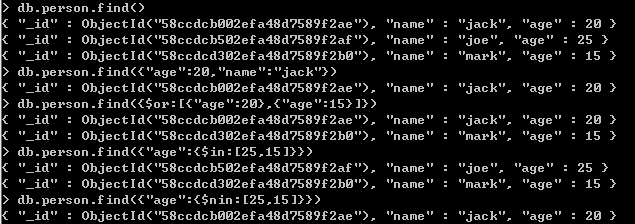
关键路径
AOE网:在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,
这种有向图的边表示活动的网,我们称之为AOE网(Activity On Edge Network)
始点/源点:AOE网中没有入边的顶点
终点/汇点:AOE网中没有出边的顶点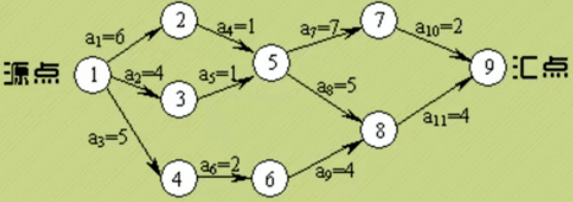
etv:时间最早发生时间,顶点的最早发生时间
ltv:事件最晚发生时间,每个顶点对应事件最晚需要开始的时间,如果超出此时间将会延误着整个工期
ete:活动最早开工时间,弧的最早发生时间
lte:活动最晚发生时间,不推迟工期的最晚开工时间
关键路径的目的是在规划工程各项活动执行的顺序时,找出关键的活动,保证工程不延期

代码链接