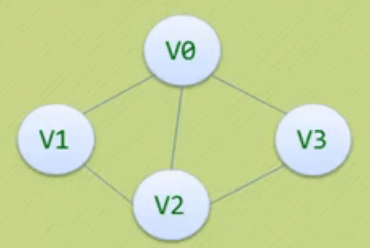
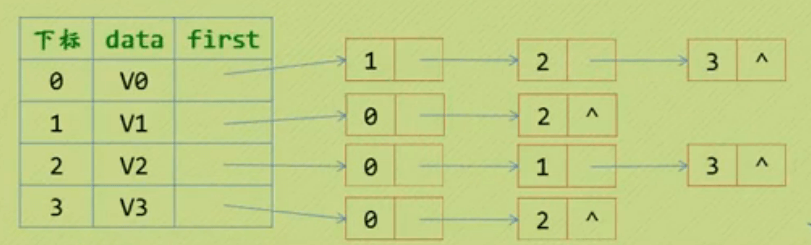
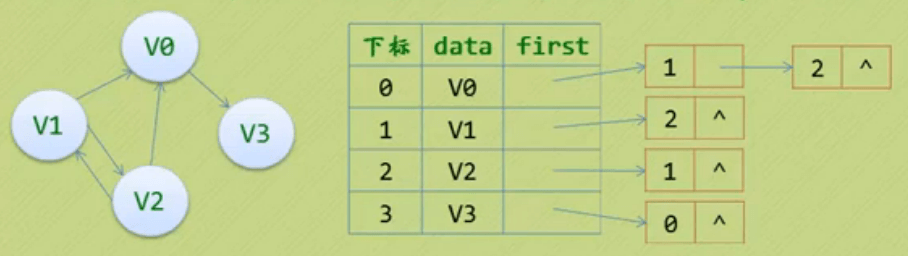
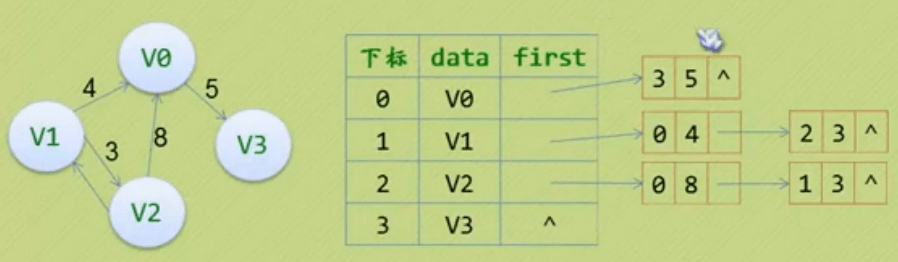
作用域
不通过花括号来界定,通过函数来定义,1
2
3
4if(true){
var somevar = "value";
}
console.log(somevar);//value
在访问未定义的变量或定义了但没有初始化的变量时都会获得undefined1
2
3
4
5var scope = "1111";
var f = function(){
console.log(scope); //undefined
var scope = 'f';
}
作用域的嵌套关系在定义时确定,不在调用时确定1
2
3
4
5
6
7
8
9
10var scope = "top";
var f1 = function(){
console.log(scope);
};
f1();//top
var f2 = function(){
var scope = 'f2';
f1();
};
f2(); //top
全局作用域是个对象,这个对象叫全局对象,nodejs是global对象,浏览器是window对象,包括
在最外层定义的变量
全局对象的属性
未用var定义直接赋值的变量
闭包
由函数(环境)及其封闭的自由变量组成的集合体,
可以想象成一个容器,里面包括一个函数和它用到的变量,每当想使用一次这个容器里的函数,就将这个容器复制一次给调用者:
1.不通调用者得到的容器相互隔离,没有关系,
2.被复制到调用者的函数,会自己形成一个独立的运行环境,每次调用完会根据变量性质,更新变量值,不会释放变量1
2
3
4
5
6
7
8
9
10
11
12
13
14var generateClosuer = function() {
var count = 0;
var get = function(){
count++;
return count;
}
return get;
}
var counter1 = generateClosuer();
var counter2 = generateClosuer();
console.log(counter1()); //1
console.log(counter1()); //2
console.log(counter2()); //1
console.log(counter1()); //3
对象
上下文对象即this指针,即被调用函数所处的环境,
上下文对象的作用是在一个函数内部引用调用它的对象本身。1
2
3
4
5
6
7
8function User(name,url){
this.name = name;
this.url = url;
this.diaplay = function(){
console.log(this.name);
}
}
var someuser = new User('byvoid','http://www.byvoid.com');
创建someuser对象时,构造函数的this指调用它的someuser
函数类型的变量指向这个函数实体的一个引用,在引用之间赋值不会对对象产生复制行为。
我们可以通过函数的任何一个引用调用这个函数,但该函数的上下文即this不同1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16var someuser = {
name:'byvoid',
func: function(){
console.log(this.name);
}
};
var foo = {
name:'foobar'
};
someuser.func();//byvoid
foo.func = someuser.func; //引用someuser.func这个函数实体,其实就是someuser.func的代码内容
foo.func();//foobar this是foo
name = 'global';
func = someuser.func;
func();//global
call/apply
让其他对象调用本对象的方法
A对象名.函数属性名.call(B对象名,函数参数表(逗号隔开)); //B调用A的方法
A对象名.函数属性名.apply(B对象名,函数参数数组);//B调用A的方法
bind
永久绑定函数的上下文,使其无论被谁调用,上下文都是固定的
A对象名.函数属性名.bind(B对象名,函数参数表(逗号隔开));
bind方法返回上下文为B对象的A对象的函数
如果在使用bind时,绑定了参数表,则在调用返回函数时,只需要传入未绑定的参数即可
注意不能重复绑定1
2
3
4
5
6
7
8
9
10
11
12
13
14var someuser = {
name:'byvoid',
func:function(){
console.log(this.name);
}
};
var foo = {
name:'foobar'
};
func = someuser.func.bind(foo);
func();//foobar
func2 = func.bind(someuser);
func2();//foobar;
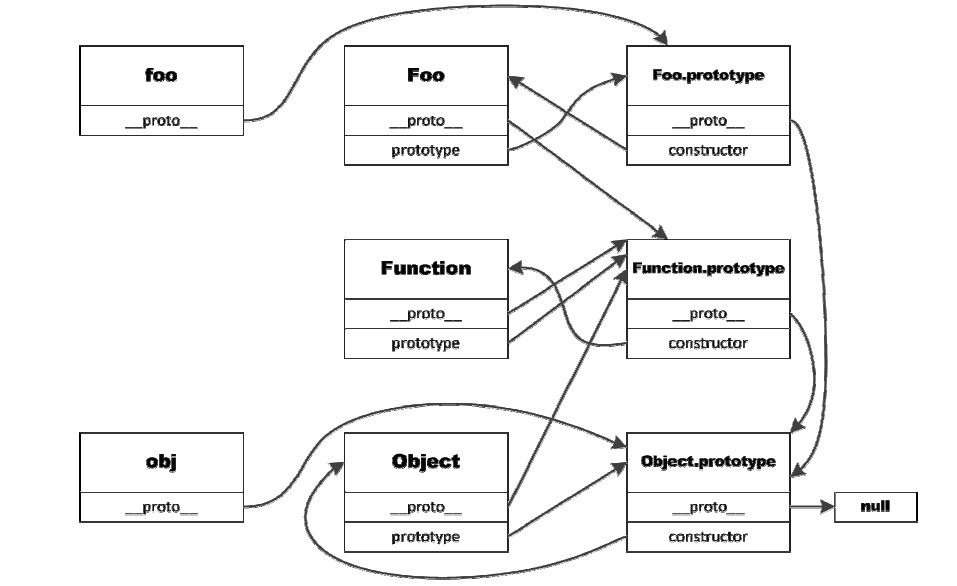
原型
构造函数创建属性
除非必须用构造函数闭包,否则尽量用原型定义成员函数
原型定义的成员是多个实例共享的,因此尽量在构造函数内定义一般成员尤其是对象或数组
原型链1
2
3
4
5
6
7
8
9
10
11function Foo(){
}
object.prototype.name = 'my object';
Foo.prototype.name = 'Bar';
var obj = new object();
var foo = new Foo();
console.log(obj.name);//my object
console.log(foo.name);//Bar
console.log(foo.__proto__.name);//Bar
console.log(foo.__proto__.__proto__.name);//my object
console.log(foo.__proto__.constructor.prototype.name);//Bar
【广发证券nodejs应用](http://slides.com/loskael/node#/)