1.邻接矩阵
1.无向图
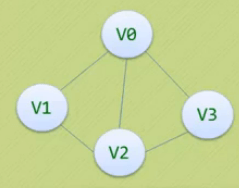
一个一维数组存储图中顶点信息,
| 顶点数组 | v0 | v1 | v2 | v3 |
|---|---|---|---|---|
一个二维数组(邻接矩阵)存储图中边或弧的信息
0表示不存在顶点间的边,1表示顶点间存在边
| v0 | v1 | v2 | v3 | |
|---|---|---|---|---|
| v0 | 0 | 1 | 1 | 1 |
| v1 | 1 | 0 | 1 | 0 |
| v2 | 1 | 1 | 0 | 1 |
| v3 | 1 | 0 | 1 | 0 |
无向图构成的邻接矩阵为对称矩阵,对角线值为0
—–顶点Vi在邻接矩阵中第i行(或第i列)的元素之和为该顶点的度
—–扫描矩阵中第i行元素,元素为1的列为顶点Vi的邻接点
2.有向图
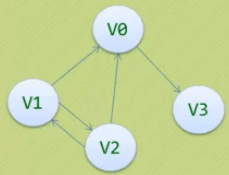
一个一维数组存储图中顶点信息,
| 顶点数组 | v0 | v1 | v2 | v3 |
|---|---|---|---|---|
坐标[Vi][Vj]的值,1表示Vi指向Vj的弧存在,0表示不存在
| v0 | v1 | v2 | v3 | |
|---|---|---|---|---|
| v0 | 0 | 0 | 0 | 1 |
| v1 | 1 | 0 | 1 | 0 |
| v2 | 1 | 1 | 0 | 0 |
| v3 | 0 | 0 | 0 | 0 |
第Vi列的元素之和为顶点Vi的入度
第Vi行的元素之和为顶点Vi的出度
3.网
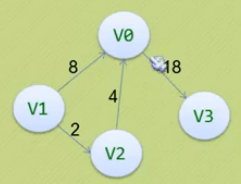
邻接矩阵各元素的值不再用0/1表示,而是用权表示
顶点间若不存在弧,则用\infty无穷表示,顶点自己到自己的权为0
| v0 | v1 | v2 | v3 | |
|---|---|---|---|---|
| v0 | 0 | \infty | \infty | 18 |
| v1 | 8 | 0 | 2 | \infty |
| v2 | 4 | \infty | 0 | \infty |
| v3 | \infty | \infty | \infty | 0 |
2.邻接表
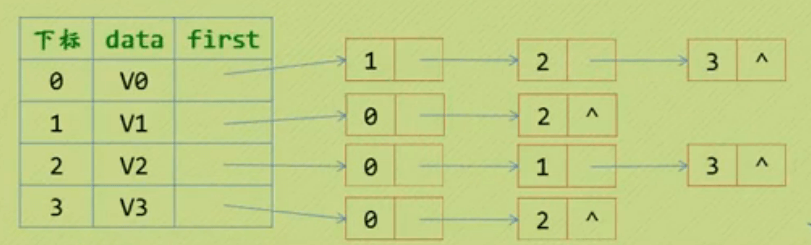
无向图
顶点用一个一维数组存储
每个顶点Vi的所有邻接点构成一个线性表,由于个数不确定,用单链表来表示
有向图
把顶点当弧尾建立邻接表,邻接表长度就是该顶点出度
把顶点当弧头建的表叫逆邻接表,邻接表长度就是该顶点入度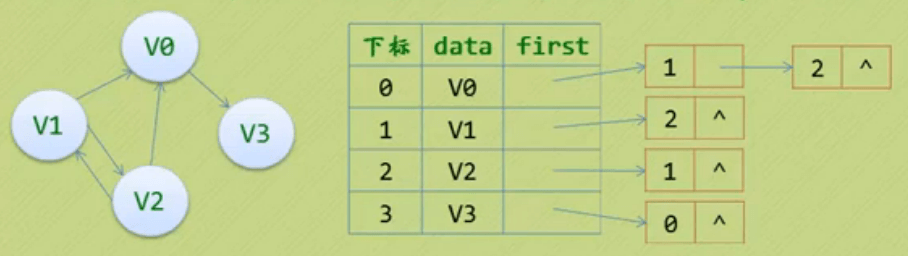
网
在边表结点定义中再增加一个数据域来存储权值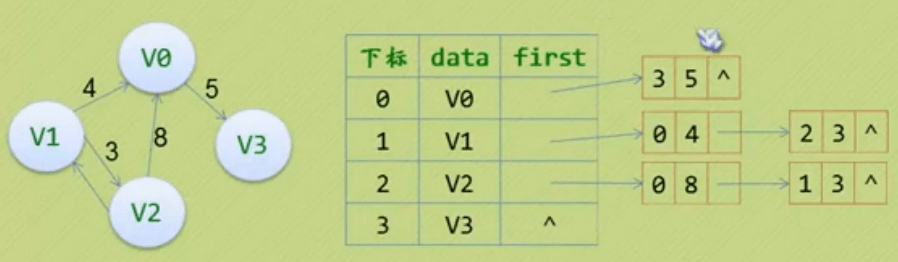
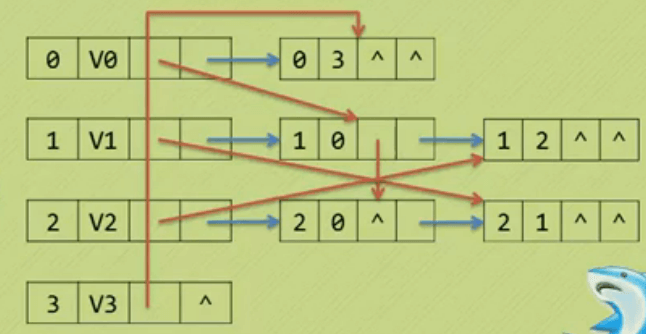
3.十字链表(有向图)
顶点表结构
|data|firstIn|firstOut|
data:顶点数据
firstIn:第一个入边表的指针
firstOut:第一个出边表的指针
边表结点结构 表示以条边
| tailVex | headVex | headLink | tailLink |
|---|---|---|---|
tailVex:该弧起点的顶点在顶点表的下标
headVex:该弧终点的顶点在顶点表的下标
headLink:指向headVex的弧的指针
tailLink: 从tailVex出发的弧的指针
4.邻接多重表(无向表)
关注对象是图中的表不是顶点
|iVex|iLink|jVex|jLink|
iVex和jVex是与某条边依附的两个顶点在顶点表中的下标
iLink:指向依附顶点iVex的下一条边,
jLink:指向依附顶点jVex的下一条边,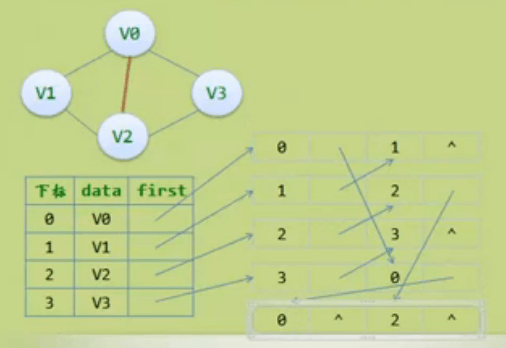
5.边集数组
由两个一维数组构成
一个是存储顶点的信息
另一个存储边的信息
边数组的每个数据元素由一条边的起点下标(begin)、终点下标(end)和权(weight)组成
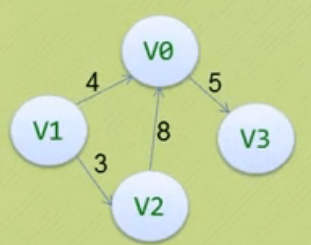
| 顶点数组 | v0 | v1 | v2 | v3 |
|---|---|---|---|---|
| 边数组 | begin | end | weight |
|---|---|---|---|
| edges[0] | 0 | 3 | 5 |
| edges[1] | 1 | 0 | 4 |
| edges[2] | 1 | 2 | 3 |
| edges[3] | 2 | 0 | 8 |