关于树的一些定义

树

定义：n(n>=0)个结点的有限集。当n=0时称为空树，在任意一颗非空树中：
——有且仅有一个特定的结点称为根
——当n>1时，其余结点可分为m(m>0)个互不相交]的有限集T1、T2…Tm,其中每一个集合本身又是一颗树，并且称为根的子树
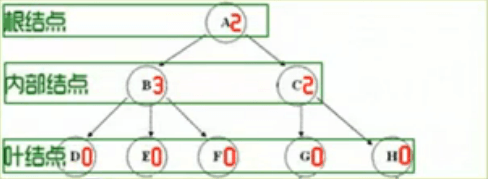
结点：图中每一个圆圈称为树的一个结点
结点的度：结点拥有的子树数称为该结点的度
树的度：树内各结点度的最大值
叶结点/终端结点：度为0的结点
分支结点/非终端结点：度不为0的结点
内部结点：分支结点中除根节点以外的结点
结点的孩子：D是B的孩子
孩子的双亲：B是D的双亲
兄弟：D和E互称为兄弟
结点的祖先：从根到该结点所经过分支上的所有结点
结点的层次：从根开始定在一起,根为第一层，根的孩子为第二层
树的深度/高度：树中结点的最大层次,图中树的深度为3
有序树:如果将树中结点的各子树看成从左至右是有次序的不能互换的，则称该树为有序树，否则称为无序树
森林:m(m>=0)棵互不相交的树的集合。对树中每个结点而言，其子树的集合即为森林

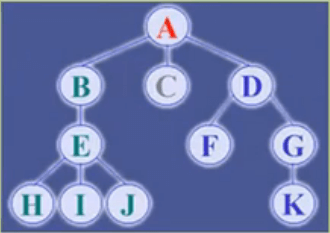
以下遍历采用层序遍历

双亲表示法

每个结点由该结点数据和该结点双亲的下标组成,根结点双亲下标赋值为-1

下标	data	parent
0	A	-1
1	B	0
2	C	0
3	D	0
4	E	1
5	F	3
6	G	3
7	K	6
8	H	4
9	I	4
10	J	4

孩子表示法

每个结点由该结点数据和该结点双亲的下标、该结点孩子的下标组成,根结点双亲下标赋值为-1
无孩子则孩子属性赋值-1

下标	data	parent	children
0	A	-1	1,2,3
1	B	0	4
2	C	0	-1
3	D	0	5,6
4	E	1	8,9,10
5	F	3	-1
6	G	3	-1
7	K	6	-1
8	H	4	-1
9	I	4	-1
10	J	4	-1

兄弟表示法

每个结点由该结点数据和该结点双亲的下标、该结点兄弟的下标组成,根结点双亲下标赋值为-1
无兄弟则兄弟属性赋值-1

下标	data	parent	rightsib
0	A	-1	-1
1	B	0	2
2	C	0	3
3	D	0	-1
4	E	1	5
5	F	3	6
6	G	3	-1
7	K	6	-1
8	H	4	9
9	I	4	10
10	J	4	-1

双亲孩子表示法

所有结点组成一个数组，每个结点包含该结点数据属性,该结点双亲属性(由双亲结点下标表示)以及第一个孩子结点的下标
每一个孩子结点包含下一个孩子结点的下标,用js数组实现相当于兄弟表示法

下标	data	parent	nextchildren
0	A	-1	-1
1	B	0	2
2	C	0	3
3	D	0	-1
4	E	1	5
5	F	3	6
6	G	3	-1
7	K	6	-1
8	H	4	9
9	I	4	10
10	J	4	-1

# define MAX_TREE_SIZE 100
typedef char ElemType;
//孩子结点
typedef struct
{
	int child;						//孩子结点的下标
	struct CTNode *next;	//指向下一个孩子结点的指针
}*ChildPtr;

//表头结构
typedef struct
{
	ElemType data;				//存放在树中的结点数据
	int parent;						//存放双亲的下标
	ChildPtr firstchild;	//指向第一个孩子的指针
}
//树结构
typedef struct
{
CTBox nodes[MAX_TREE_SIZE];//结点数组
int r,n;
}

js实现：

var tree=[];
for(var i =0;i<11;i++){
  var prior = -1;
  var next = [];
  if(i==0){
    prior =-1;
  }else if(i>0&&i<4){
    prior = 0;
  }else if(i==4){
    prior = 1;
  }else if(i==5 || i==6){
    prior = 3;
  }else if(i>6 && i<10){
    prior = 4;
  }else{
    prior = 6;
  }
  tree.push({
    data:i,
    parent:prior,
  });
}
for(var i =0;i<11;i++){
 var children=[];
  for(var j =0;j<11;j++){
   if(tree[j].parent == i){
     children.push(j);
   }
  }
  tree[i].children = children.slice();
}
console.log(tree);