二叉树
定义
定义:是n(n>=0)个结点的有限集合,该集合或者为空集(空二叉树),或者由一个
根节点和两颗不互相交的、分别称为根的左子树和右子树的二叉树
特点:
-每个结点最多有两颗子树,不存在度大于2的结点
-左右子树有顺序,次序不能颠倒,即使只有一颗子树也要区分它是左子树还是右子树
五种基本形态:
空二叉树
只有一个根节点
根结点只有左子树
根结点只有右子树
根结点既有左子树又有右子树
特殊二叉树
1.斜树:只有左子树或只有右子树
2.满二叉树:该二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上
–特点:
1.叶子只能出现在最下一层
2.非叶子结点的度一定是2
3.在同样深度的二叉树中,满二叉树的节点个数一定最多,同时叶子也最多
3.完全二叉树:对一颗具有N个结点的二叉树按层序编号,如果编号为i(i<=i<=n)的结点与同样深度的满二叉树中编号为i的
结点位置完全相同,则这棵树称为完全二叉树
–特点:
1.叶子结点只能出现在最下两层
2.最下层的叶子一定集中在左部连续位置
3、倒数第二层,若有叶子结点,一定都在右部连续位置
4.如果结点度为1,则该结点只有左孩子
5.同样结点数的二叉树,完全二叉树的深度最小
满二叉树一定是完全二叉树,但完全二叉树不一定是满二叉树
二叉树存储结构
顺序结构
用数组存储,按层序遍历对比满二叉树顺序,没有结点的位置数组在该位置填空
二叉链表
每个结点包含一个数据域和两个指针域,两个指针分别指向该结点左右孩子结点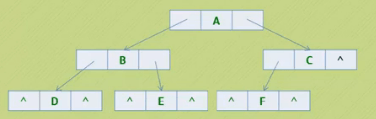
1
2
3
4
5typedef struct BiTNode
{
ElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,8BiTree;
二叉树的遍历
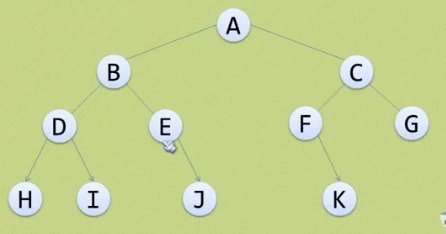
从根结点出发,按照某种次序访问二叉树中所有结点,使每个结点被访问一次且仅被访问一次
1.前序遍历:根左右
若二叉树为空,则空操作返回;否则先访问根结点,然后前序遍历左子树,再前序遍历右子树
a.先访问根结点,然后访问根结点的左孩子
b.将根结点的左孩子视作子树根结点,继续访问其左孩子,再以这个左孩子结点为根再访问其左孩子直到叶结点
c.访问完该叶结点后,再访问该叶结点双亲的右孩子,
d.如果没有右孩子,则该子树访问完毕,继续访问该结点双亲的双亲的右孩子,再以该右孩子为根继续从步骤a开始访问
核心:从整棵树的根结点开始,每次将左孩子看成子树根结点,从上到下,从左到右
ABDHIEJCFKG
2.中序遍历 :左根右
若二叉树为空,则空操作返回;否则从根节点根结点开始(并不是先访问根结点),然后中序遍历左子树,然后访问根结点,再中序遍历右子树
核心:无论什么级别的子树树都从最左端叶结点开始,按左孩子,双亲,右孩子顺序遍历,从下到上,从左到右
HDIBEJAFKCG
3.后序遍历 :左右根
若二叉树为空,则空操作返回;否则从左到右先叶子结点的方式遍历左右子树,最后访问根结点
核心:从最左端叶结点开始,按左孩子,右孩子,双亲顺序遍历,从左到右,从下到上
HIDJEBKFGCA
4.层序遍历
若二叉树为空,则空操作返回;否则从根节点开始,按层依次往下,每层从左到右依次遍历
二叉树的性质
性质一:在二叉树的第i层上至多有2^(i-1)个结点(i>=1)
性质二:深度为K的二叉树至多有2^K-1个结点(K>=1)
性质三:对于任何一颗二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1
性质四:具有n个结点的完全二叉树的深度为log2n取下限加1
性质五:如果对一颗有n个结点的完全二叉树(其深度为log2n取下限加1)的结点按层序编号对任一结点i(1<=i<=n)有以下性质
如果i=1,则结点i是二叉树的根,无双亲;如果i>1,则其双亲是结点i/2取下限
如果2i>n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i
如果2i+1>n,则结点i无右孩子(结点i为叶子结点);否则其右孩子是结点2i+1
计算:
输出指定结点在该树中所在的层数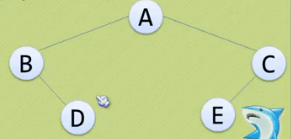
[未完成]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35var str="AB DEC #";//约定前序遍历输入
var btree = {
data:'',
lchild:{},
rchild:{}
};
console.log(btree);
function creatbtree(num,item){
console.log(str[num])
if(str[num]=="#");
{
return
}
if(str[num] == " "){
item = null;
}else{
item.data = str[num];
num+=1;
item.lchild ={
data:'',
lchild:{},
rchild:{}
}
creatbtree(num,item.lchild);
num+=1;
item.rchild ={
data:'',
lchild:{},
rchild:{}
}
creatbtree(num,item.rchild);
}
}
creatbtree(0,btree);
console.log(btree.rchild)