My Little World

逆波兰表达式/后缀表达式

发表于

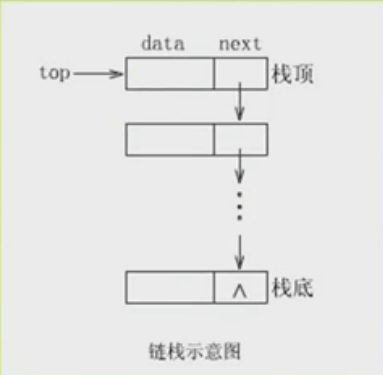
栈的链式存储结构

栈的链式存储结构

stack2

1
2
3
4
5
6
7
8
typedef struct StackNode{
  ElemType data;          ##存放栈的数据
  struct StackNode *next;
}StackNode,*LinkStackPtr;
typedef struct LinkStack{
  LinkStackPrt top;        ##top指针
  int count;               ##栈元素计数器
}

栈链的入栈操作

假设元素值e的新结点是s,top为栈顶指针

1
2
3
4
5
6
7
8
Status Push(LinkStack *s,ElemType e){
  LinkStackPtr p=(LinkStackPtr)malloc(sizeof(StackNode));
  p->data = e;
  p->next = s->top;
  s->top = p;
  s->count++;
  return OK;
}

栈的出栈操作

假设变量p用来存储要删除的栈顶结点，将栈顶指针下移一位，最后释放p

1
2
3
4
5
6
7
8
9
10
11
12
Status Pop(LinkStack *s,ElemType e){
  LinkStackPtr p;
  if(StackEmpty(*s)){
  return ERROR;
  }
  *e=s->top->data;
  p=s->top;
  s->top = s->top->next;
  free(p);
  s->count--;
  return OK;
}

逆波兰表达式/后缀表达式

正常表达式–>后缀表达式
（1-2)x(4+5）–> 1 2 - 4 5 + x
1.计算后缀表达式
主要思想是判断字符是否为运算符，若为数字，则入栈，为运算符则连续出栈两次进行运算，再将运算结果入栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
var list =[1,2,3,4,'-','*','+']
var stack = [];
for(var i = 0;i<list.length;i++){
  if(!isNaN(list[i])){
      stack.push(list[i]);
    }else{
       var a = stack.pop();
       var b = stack.pop();
       if(list[i] =="+"){
        stack.push(b+a);
       }else if(list[i] =="-"){
        stack.push(b-a);
       }else if(list[i] =="*"){
        stack.push(b*a);
       }else if(list[i] =="/"){
        stack.push(b/a);
       }
  }
}
console.log(stack);

2.计算表达式转后缀表达式
主要思路
1，表达式中参与运算的数字、运算符以及小括号分割，形成待处理数组
2，循环判断
A.若字符为数字，入栈2，
B.若字符为“+”、“-”，分情况讨论
（1）此时栈1为空，入栈；
（2）栈1不为空，将“（”左括号以上的符号从栈1 pop到栈2，“（”留 在栈1，处理完后，将“+”、“-”入栈1；
C若字符为“）”，将“（”以上符号从栈1 pop到栈2，“（”也pop出来
但不入栈2
D若字符为“/”“*”“（”直接入栈2
E其他情况，非法字符，抛出异常
3.将栈1元素pop到栈2；
栈2即后缀表达式
代码链接