排序

记录：在排序问题中，通常将数据元素称为记录
–输入一个记录集合，排序后输出也是一个记录集合
–将排序看成是线性表的一种操作
排序依据关键字之间的大小关系，那么对同一记录集合，针对不同的关键字进行排序，可以得到不同的序列

排序稳定性

假设Ki=Kj(1<=i<=n,1<=j<=n,i!=j),且在排序前的序列中ri领先于rj(即i<j)
–如果排序后ri仍领先于rj,则称所用排序方法是稳定的
–反之，若排序后rj仍领先于ri,则称所用排序方法是不稳定的
即原来值相同的两个值A和B,排序前A在B前面，排序后位置不变则说排序算法是稳定的，否则是不稳定的

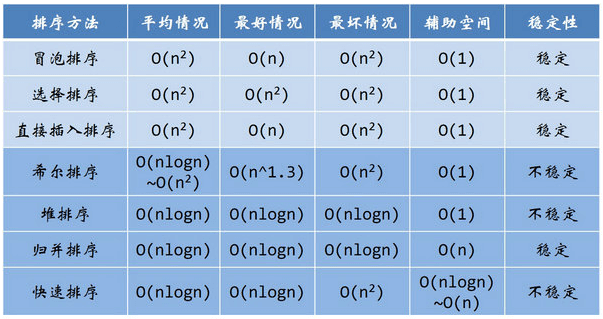
影响排序算法性能的几个要素

时间性能(比较，移动)
辅助空间(存放临时变量)
算法的复杂性

冒泡排序算法n^2

两两相邻记录的关键字，如果反序则交换，直到没有反序记录为止
注意点：
– 每次比较相邻两个元素
– 如果有n个元素,比较n-1次，每次减少1次比较
– 从下往上比较，即从后往前比较
代码链接

选择排序法n^2

通过n-i次关键字间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i(1=<i<=n)个记录交换
代码链接

直接插入排序n^2

连续两个值比较若后面的比前面的小，就将后面的值移到比它大的值的前面
适用于记录本身就是有序的,记录数少
代码链接

希尔排序n*logn

将所有元素按一定间隔f取出n/f个进行比较，再按顺序放回对应的位置，直到所有元素参与完比较之后，算完成一轮比较，
再改变间隔进行下一轮比较，直到间隔为1
可以将该处理方法套进冒泡、选择和直接插入的方法中
代码链接

堆排序n*logn

大顶堆；每个结点大于等于其左右孩子的完全二叉树
小顶堆：每个结点小于等于其左右孩子的完全二叉树
各结点一定是堆中所有结点的最大或最小者，如果按照层序遍历方式给结点从1开始编号，则结点之间满足如下关系
大顶堆：Ki>=K2i && Ki>=K2i+1
大顶堆：Ki<=K2i && Ki<=K2i+1
其中(1<=i<=n/2取下限)
下标i与2i和2i+1是双亲和子女关系
堆排序：利用堆进行排序
– 将待排序的序列构造成一个大顶堆(从小到大)(或小顶堆(从大到小))
– 此时整个序列的最大值就是堆顶的根结点。将它移走(就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)
– 然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的此最大值
– 如此反复执行，便能得到一个有序序列了
代码链接

归并排序

将待排序数组每次一份为2，直到每一份的数组长度为1，
对拆分的两份结果排序合成一个新数组，参与下次下一次比较排序合并
代码链接

快速排序

每趟排序指定一个基准点，把比基准点小的元素放在基准点左边，比基准点大的元素放在基准点右边
再以基准点为界，把前面的数据(都比基准点小)和后面的数据(都比基准点大)按两部分的最小下标为基准准进行移动,
优化
选取基准点
不必要的交换
小数组时的排序方案(使用直接插入排序)
递归操作
尾递归：函数递归形式的调用出现在函数末尾，可以大大缩减栈空间
代码链接

小结

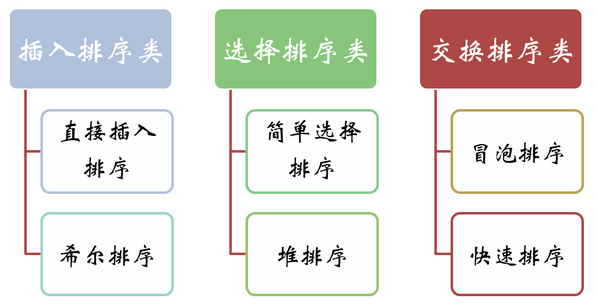
插入排序类:直接插入排序、希尔排序
选择排序类：选择排序、堆排序
交换排序类：冒泡排序、快速排序
归并排序类：归并排序