My Little World

拓扑排序

发表于

背景

DAG(Directed Acyclic)图/无环图：无环的有向图
‘活动’：所有的工程或者某种流程都可以分为的若干个小的工程或者阶段
AOV(Active On Vertex Network)网：在一个表示工程的有向图中，用顶点表示活动，用弧表示活动之间的优先关系
这样的有向图为顶点表示活动的网即AOV网
拓扑序列：设G=(V,E)是一个具有n个顶点的有向图，V中的顶点序列V1，V2，……Vn满足若从顶点Vi到Vj有一条路径，则在顶点序列中顶点Vi必在顶点Vj之前,我们称这样的顶点序列为一个拓扑序列,
拓扑排序：所谓的拓扑排序，其实就是对一个有向图构造拓扑序列的过程,保证活动是按一定顺序进行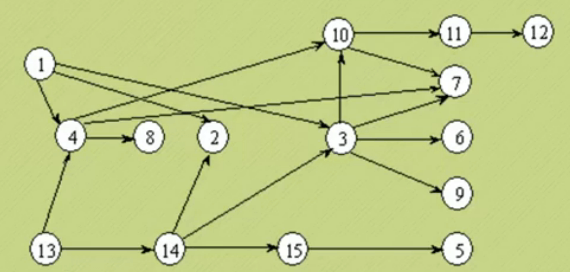
tuopu1

对AOV网进行拓扑排序的方法和步骤

——从AOV网中选择一个没有前驱的顶点(入度为0的顶点),并且输出它；
——从网中删去该顶点，并且删去从该顶点发出的全部有向边(将有向边终点入度减一)
——重复上述两步，直到剩余网中不再没有前驱的顶点为止。
代码链接

算法时间复杂度

对一个具有n个顶点，e条边的网来说，初始建立入度为0的顶点栈，要检查所有顶点一次，执行时间为O(n);
排序中，若AOV网无回路，则每个顶点入、出栈各一次，每个表结点被检查一次，因而执行时间是O(n+e);
因此整个算法时间复杂度是O(n+e)